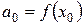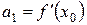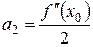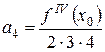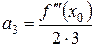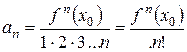Метод знаходження інтервала збіжності степеневого ряду
Нехай дано степеневий ряд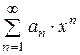 
. Для знаходження інтервала збіжності застосовують ознаку Д’Аламбера.
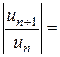
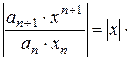
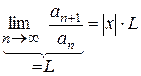
Для того, щоб ряд був збіжним, потрібно, щоб одержаний вираз був меншим 1, тобто
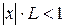
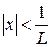
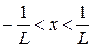- інтервал збіжності ряду
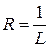
Для знаходження області збіжності потрібно дослідити поведінку ряду на кінцях інтервалу. Для цього замість х в степеневий ряд підставляють значення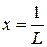 
і 
і 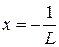досліджують одержані числові ряди на збіжність.
Приклад: знайти область збіжності степеневого ряду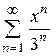 
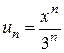
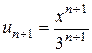
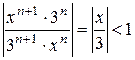
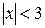
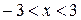- інтервал збіжності
R = 3
Перевіримо поведінку ряду на кінцях інтервалу:
а) при х = 3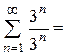 
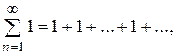не виконується необхідна ознака збіжності, тобто 
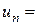
1=1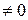 
, отже ряд розбіжний.
Значить правий кінець інтервалу не входить в область збіжності.
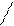
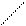б) при х = - 3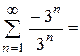 
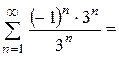
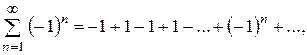
одержали ряд, знаки якого строго чергуються; застосуємо ознаку Лейбніца:
1 = 1=1 = ... – модулі членів ряду не спадають, значить ряд розбіжний.
Тобто, лівий кінець інтервалу не входить в область збіжності.
Відповідь: областю збіжності степеневого ряду є інтервал ( - 3; 3)
 |
розб збіг розб
- 3 0 3 х
2. Розглянемо степеневий ряд за степенями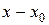 
:
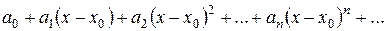
Нехай функція f (x) є сумою ряду на інтервалі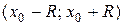 
:
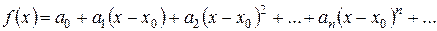
Нехай існують всі похідні функції f (x) і значення самої функції в точці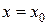 
. Знайдемо коефіцієнти цього ряду, послідовно диференцюючи ряд і підставляючи в знайдені похідні значення .
|
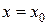Знайдемо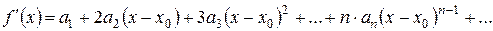 
|
|
| ||||
| ||||
...
|
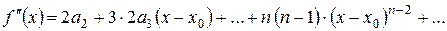
Тоді
Степеневий ряд прийме вигляд:
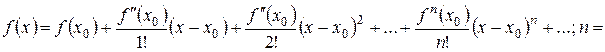0, 1, 2, ... – ряд Тейлора.
Теорема (про достатні умови розкладання функції в ряд Тейлора)
Якщо функція f (х) в інтервалі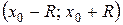 
має похідні всіх порядків та існує число M > 0 таке, що модуль кожної похідної буде меншим від М.
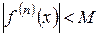, то функцію f (x) можна розкласти в ряд Тейлора.
Якщо в ряді Тейлора приймемо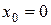 
, то одержимо ряд Маклорена:
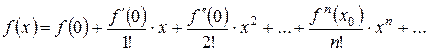
Степеневі ряди застосовуються для наближених обчислень, для розв’язування диференціальних рівнянь, для обчислення визначених та невизначених інтегралів.
3. Щоб функцію f (x) розкласти в ряд Маклорена, потрібно:
1) знайти похідні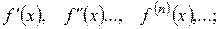 
2) обчислити значення похідних в точці х = 0
3) записати ряд Маклорена для даної функції і знайти інтервал його збіжності;
4) визначити інтервал ( - R; R) в якому залишковий член формули Маклорена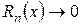 
при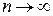 
.
Приклади:
1) 
...
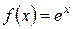
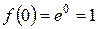
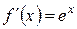
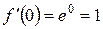
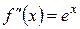
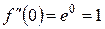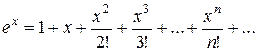
Область збіжності ряду
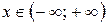
2) 
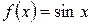
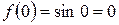
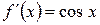
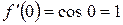
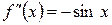
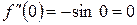
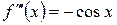
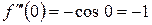
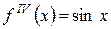
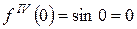
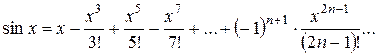
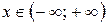
3) 
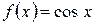
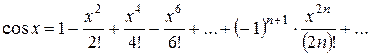
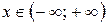
4) Біноміальний ряд
, 
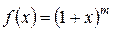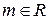
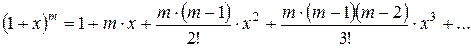
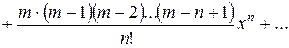
Область збіжності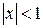 
5) 
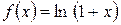
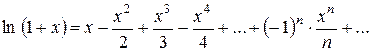
n = 0, 1, 2, ...
Область збіжності ( -1; 1]
6) 
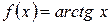
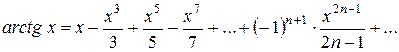
n = 1, 2, 3 …
Область збіжності [ -1; 1]
Завдання додому
1) Конспект; [1] с. 512 – 527
Питання для самоконтролю
1. Теорема Абеля. Радіус збіжності ряду.
2. Ряди Тейлора та Маклорена.
3. Розвинення елементарних функцій у степеневий ряд.
Лекція 34
Тема: Ряди Фур¢є
Мета: ознайомити з тригонометричним рядом Фур¢є, комплексною формою ряду Фур¢є інтегралами Фур¢є.
Література: [1, с. 538-564]; [6., с. 508-510].
П Л А Н
1. Тригонометричний ряд Фур¢є, коефіцієнти Фур¢є.
2. Розкладання функції у ряд Фур¢є
І. Означення.Функція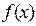 
називається такою, що задовольняє умови Діріхле на відрізку[a;b], якщо на цьому відрізку виконуються такі умови:
1. 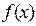має скінченне число розривів першого роду;
2. 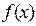має скінченне число екстремумів;
3. 
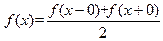для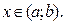 
Теорема. Функц і я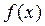 
, що задовольняє умови Діріхле на відрізку [- 
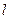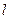; ] на інтервалі(- 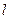; 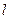) , може бути визначена тригонометричним рядом Фур ¢ є:
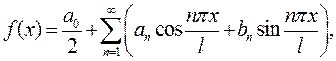(1)
де коефіцієнти Фур ¢ є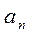 
та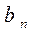 
обчислюються за такими формулами:
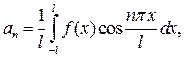
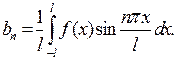
Зауваження.Якщо функція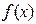 
– парна, то в (1) 
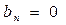, а якщо
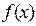– непарна, то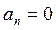 
Теорема. (ознака Діріхле). Якщо 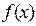– періодична функція з періодом 2 
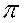задовольняє умови Діріхлє на відрізку [- 
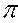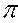; ], то її ряд Фур ¢ є збіжний, а його сума в точці 
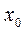дорівнює:
1. 
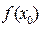, якщо 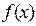– неперервна в точці 
;
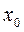2. 
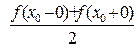, якщо 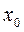– точка розриву для 
.
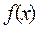Приклад. Розкласти функцію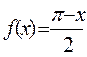 
у ряд Фур¢є на проміжку (0;2 
).
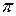Ця функція на відрізку [0;2 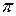] задовольняє умови Діріхле, а тому ряд Фур¢є на інтервалі (0;2 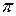) для неї існує. Обчислимо коефіцієнти Фур¢є, узявши 
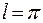в (1):
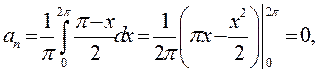
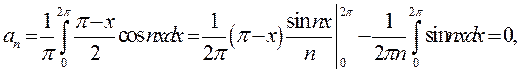
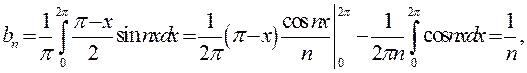
Отже,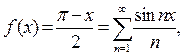 
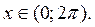
Питання для самоконтролю
1. Тригонометричний ряд Фур¢є, коефіцієнти Фур¢є.
2. Розкладання функції у ряд Фур¢є
Л Е К Ц І Я 35
Тема: Елементи математичної економіки
Мета: сформувати поняття арифметичної прогресії та простих відсотків, геометричної прогресії та складних відсотків, розглянути застосування понять до розв’язування економічних задач.
Література: [2, с. 450-472]; [4, с. 385-396].
П Л А Н
1. Арифметична прогресія та прості відсотки
2. Властивості арифметичної прогресії
3. Поняття простих відсотків та капітал
4. Геометрична прогресія та складні відсотки
5. Властивості геометричної прогресії
6. Поняття складних відсотків та капітал
1. Означення. Арифметичною прогресією називається числова послідовність, кожен член якої, починаючи з другого, дорівнює попередньому члену, доданого до певного сталого для даної послідовності числа d , яке називається різницею прогресії. Арифметичну прогресію позначають ÷
У випадку d > 0 арифметичну прогресію називають зростаючою, а при d < 0 – спадною.
За означенням арифметичної прогресії маємо an +1 = an + d , n Є N .