Алгоритми перевірки на абсолютну збіжність.
1) Утворюється ряд з модулів членів даного ряду.
2) Якщо цей ряд збіжний, то значить ряд збігається абсолютно.
3) Якщо цей ряд розбіжний, то даний ряд перевіряють на збіжність за ознакою Лейбніца. Якщо даний ряд збіжний, то він збігається умовно.
Приклад: Абсолютно чи умовно збігається ряд:
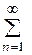
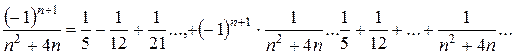
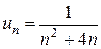
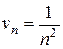 - ряд Діріхле (збіжний)
- ряд Діріхле (збіжний)

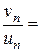

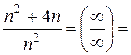

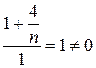
Отже, обидва ряди поводять себе однаково, значить даний ряд збігається абсолютно.
Ряди, знаки членів яких строго чергуються, застосовують для наближених обчислень значень функцій.
Завдання додому
1. Конспект; [1] с. 498 – 510
Питання для самоконтролю
1. Ряди. Основні значення.
2. Збіжність рядів, властивості збіжних рядів.
3. Необхідна умова збіжності
Л Е К Ц І Я 33
Тема: Степеневі ряди
Мета: ознайомити з теоремою Абеля, радіусом збіжності ряду. рядами Тейлора та Маклорена, розкладанням елементарних функцій в ряд Маклорена
Література: [1, с. 512-527]; [6, с. 492-504].
П Л А Н
1. Теорема Абеля. Радіус збіжності ряду.
2. Ряди Тейлора та Маклорена.
3. Розвинення елементарних функцій у степеневий ряд.
1. Означення. Ряд виду 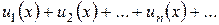 , в якому члени є функціями від
, в якому члени є функціями від 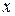 , називається функціональним рядом.
, називається функціональним рядом.
Закон зміни членів такого ряду заданий формулою n – го 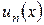 . Якщо замість х підставити значення х0 , де х = х0 – довільне число, то одержимо числовий ряд. Якщо цей ряд є збіжним, то точка х0 називається точкою збіжності функціонального ряду.
. Якщо замість х підставити значення х0 , де х = х0 – довільне число, то одержимо числовий ряд. Якщо цей ряд є збіжним, то точка х0 називається точкою збіжності функціонального ряду.
Множина всіх точок збіжності функціонального ряду називається областю його збіжності.
Частинною сумою функціонального ряду називається сума 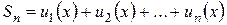 .
.
Якщо існує границя 
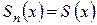 , то
, то 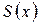 називають сумою ряду.
називають сумою ряду.
n – м залишком ряду 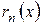 називають різницю
називають різницю 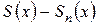 :
:
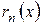 =
= 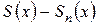
Означення. Степеневим рядом називається функціональний ряд виду
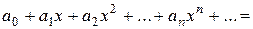
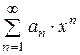 ,
,
де 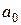 - вільний член ряду;
- вільний член ряду; 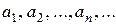 - коефіцієнти ряду.
- коефіцієнти ряду.
Теорема Абеля.
Якщо степеневий ряд 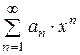 збіжний при
збіжний при 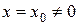 , то він абсолютно збіжний для всіх значень х, що задовольняють нерівність
, то він абсолютно збіжний для всіх значень х, що задовольняють нерівність 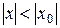 , тобто збіжний на інтервалі
, тобто збіжний на інтервалі 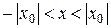 . Такий інтервал називається інтервалом збіжності ряду, а число
. Такий інтервал називається інтервалом збіжності ряду, а число 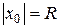 називається радіусом збіжності степеневого ряду.
називається радіусом збіжності степеневого ряду.
 |


 розб збіг розб
розб збіг розб
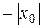 0
0 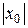 х
х
Інтервал збіжності можна записати у вигляді (- R; R)








