Властивості збіжних рядів
1) Якщо  Sn = S, то S – сума ряду.
Sn = S, то S – сума ряду.
2) Якщо ряд u1+ u2+ u3 +… + un +… збіжний, то збіжний і ряд
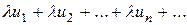 , де
, де 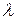 - число, причому сума такого ряду дорівнює
- число, причому сума такого ряду дорівнює 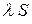
3) Нехай два ряди u1+ u2+ … + un +…
v1+ v2+ … + vn +… збіжні, тоді збіжний і ряд 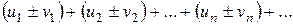 , а сума його дорівнює
, а сума його дорівнює 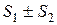 .
.
Зауваження: скорочений запис ряду
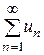 = u1+ u2+ … + un +…
= u1+ u2+ … + un +…
Приклад: Знайти суму ряду
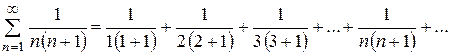
Знайдемо частинну суму Sn :
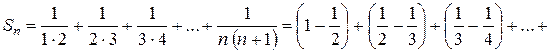
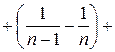
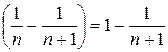
Знайдемо суму ряду:
 S=
S=  Sn =
Sn = 
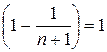
 |
0
3. Необхідна умова збіжності ряду:
Якщо ряд 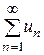 збіжний, то
збіжний, то 
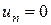
Достатня умова розбіжності ряду:
Якщо 
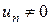 , то ряд
, то ряд 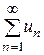 розбіжний.
розбіжний.
Приклад: Використовуючи необхідну умову збіжності, перевірити поведінку рядів:
1) 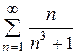 2)
2) 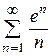 3)
3) 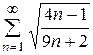
 0
0


 1)
1) 
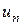 =
= 
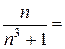

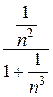 =0,
=0,
0
отже ряд може бути збіжним або розбіжним.
2) 
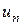 =
= 
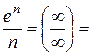

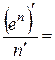

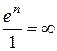 - ряд розбіжний
- ряд розбіжний
3) 
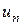 =
= 
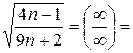

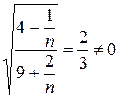 - ряд розбіжний
- ряд розбіжний
Завдання додому
Конспект; [1] с. 493 – 498,
[2] с. 356 – 362.
Л Е К Ц І Я 32
Тема: Ознаки збіжності рядів.
Мета: ознайомити з достатніми ознаками збіжності рядів з додатними членами ознаки порівняння, ознака Д’Аламбера, ознаки Коші); абсолютною та умовною збіжністю рядів; ознакою Лейбніца.
Література: [1, с. 498-505]; [6, с. 476-480].
П Л А Н
1. Достатні ознаки збіжності рядів з додатними членами (ознаки порівняння,
ознака Д’Аламбера, ознаки Коші).
2. Ознака Лейбніца.
3. Абсолютна та умовна збіжність. Теорема Коші.
1. Ознака Д’Аламбера.
Якщо для ряду з додатними членами u1+ u2+ … + un +… існує границя

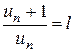 , то:
, то:
1) ряд збіжний при l < 1
2) ряд збіжний при l > 1
Якщо l = 1, то ряд може бути як збіжним, так і розбіжним. Треба дослідити ряд за допомогою інших ознак.
Ознака Д’Аламбера застосовується до тих рядів, загальний член яких містить показникову функцію 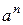 , або факторіали чисел, які залежать від n, або нескінченні добутки.
, або факторіали чисел, які залежать від n, або нескінченні добутки.
Приклад: Дослідити ряд на збіжність 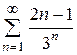
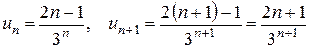

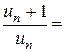

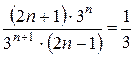

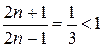 , отже ряд збіжний
, отже ряд збіжний
Зауваження: n = 1, 2, 3, 4, ...;
2n, 2n+2, 2n – 2 – запис парного числа;
2n – 1, 2n+1 – запис непарного числа;
n! = 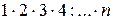 , 0!=1
, 0!=1
Ознаки порівняння
1) Нехай задано два ряди з невід’ємними членами
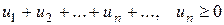 , (1)
, (1)
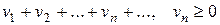 , (2)
, (2)
і для всіх n виконується нерівність 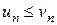
Тоді, якщо ряд (2) збіжний, то збіжний і ряд (1).Тобто, якщо збіжний ряд з більшими членами, то збіжний і ряд з меншими членами.
Якщо ж ряд (1) розбіжний, то розбіжний і ряд (2). Тобто, якщо розбіжний ряд з меншими членами, то розбіжний і ряд з більшими членами.
2) Гранична ознака порівняння.
Якщо задано два ряди з додатними членами
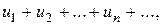
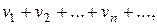
причому існує скінченна, відмінна від нуля границя відношення загальних членів двох рядів

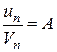
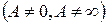 , то ряди або одночасно збіжні, або одночасно розбіжні.
, то ряди або одночасно збіжні, або одночасно розбіжні.
Для порівняння часто користуються рядами:
1) 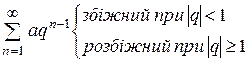
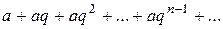 геометрична прогресія
геометрична прогресія
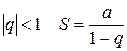
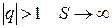
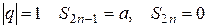
2) 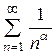
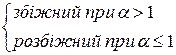
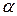 - стале число
- стале число
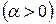
ряд Діріхле або узагальнений гармонічний ряд
3) 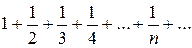 - розбіжний гармонічний ряд
- розбіжний гармонічний ряд
Приклад: Дослідити ряди на збіжність:
а) 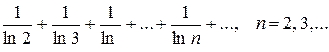
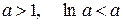
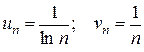 - гармонічний ряд, розбіжний
- гармонічний ряд, розбіжний
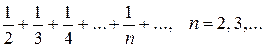
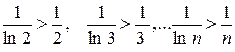
За першою ознакою порівняння даний ряд розбіжний, так як його члени більші відповідних членів гармонічного ряду, який є розбіжним.
б) 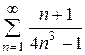
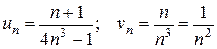 - загальний член ряду Діріхле (збіжного)
- загальний член ряду Діріхле (збіжного)

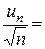

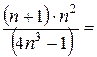

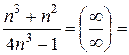

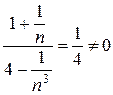
Отже, обидва ряди ведуть себе однаково, тобто даний ряд збіжний.
Ознаки Коші
1) Радикальна ознака Коші.
Якщо для ряду з додатними членами
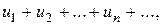
існує границя 
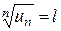 , то цей ряд збіжний при
, то цей ряд збіжний при 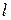 < 1 і розбіжний при
< 1 і розбіжний при 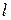 > 1.
> 1.
Якщо 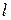 = 1, то ряд може бути як збіжним, так і розбіжним.
= 1, то ряд може бути як збіжним, так і розбіжним.
Застосовується тоді, коли можна добути корінь степеня n з un
Приклад: 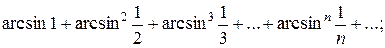
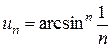 ;
;

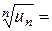

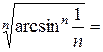

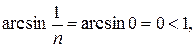
отже ряд збіжний
2) Інтегральна ознака Коші.
Нехай задано ряд
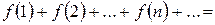
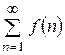 , члени якого є значеннями неперервної, додатної і монотонно спадної функції f (x) на проміжку [1; +
, члени якого є значеннями неперервної, додатної і монотонно спадної функції f (x) на проміжку [1; + 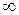 ).
).
Тоді даний ряд збіжний, якщо збіжний невласний інтеграл 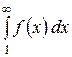 , і розбіжний, якщо цей інтеграл розбіжний.
, і розбіжний, якщо цей інтеграл розбіжний.
Приклад: 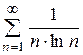
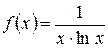
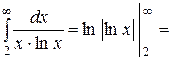

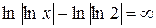 - розбіжний.
- розбіжний.
Інтегральна ознака Коші застосовується в тому випадку, коли можна знайти інтеграл від загального члена ряду.
2, 3. Розглянемо ряд, знаки членів якого строго чергуються, тобто ряд, довільні два сусідні члени якого мають різні знаки:
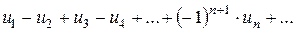 (3)
(3)
Ознака Лейбніца
Якщо члени ряду (3) спадають по модулю і загальний член ряду при 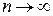 прямує до 0, то ряд (3) збіжний. Якщо ж не виконується хоча б одна з цих умов, то ряд розбіжний.
прямує до 0, то ряд (3) збіжний. Якщо ж не виконується хоча б одна з цих умов, то ряд розбіжний.
Приклад: За ознакою Лейбніца перевірити збіжність даного ряду:
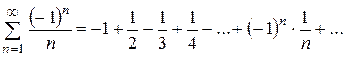
1) порівняємо члени ряду по модулю:
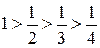 > ... – спадають
> ... – спадають
2) знайдемо 
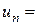

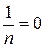
Отже, ряд збіжний.
Ряд називається знакозмінним, якщо серед його членів є як від’ємні, так і додатні.
Нехай дано ряд, знаки членів якого строго чергуються:
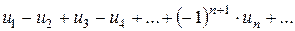
Якщо цей ряд збігається за ознакою Лейбніца і збігається ряд, утворений з модулів його членів, тобто ряд
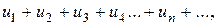 то ряд називається абсолютно збіжним.
то ряд називається абсолютно збіжним.
Якщо ж цей ряд збігається за ознакою Лейбніца , а ряд, утворений з модулів його членів, розбіжний, то ряд називається умовно збіжним.
Абсолютно збіжні ряди мають ряд важливих властивостей, наприклад, переставну властивість: будь-який ряд утворений за допомогою перестановки членів абсолютно збіжного ряду також абсолютно збіжний і має ту саму суму, що й заданий ряд. Умовно збіжні ряди переставної властивості не мають, тому що від перестановки їхніх членів може змінтися сума ряду і навіть утворитися розбіжний ряд.








