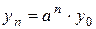2. Однорідні та неоднорідні рівняння.
Л Е К Ц І Я 30
Тема: Лінійні різницеві рівняння із сталими коефіцієнтами.
Мета: сформувати поняття різницевого рівняння порядку k; ознайомити з методами розв’язування різницевих рівнянь, застосуванням різницевих рівнянь в економіці.
Література: [1, с. 478-483]; [6, с. 441-444].
П Л А Н
1. Однорідні лінійні різницеві рівняння.
2. Неоднорідні лінійні різницеві рівняння.
1. Означення. Нехай у0, у1, у2, у3, ... – послідовність дійсних чисел. Різницевим рівнянням порядку k називають рівняння, що зв’язує у0, у1, у2, у3, ..., уn+k для кожного значення n = 0, 1, 2, 3 ...
Приклад: Визначити порядок різницевих рівнянь:
а) 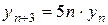 - 3-го порядку
- 3-го порядку
б) 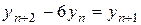 - 2-го порядку
- 2-го порядку
в) 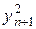 +
+ 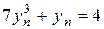 - 1-го порядку
- 1-го порядку
Розв’язком різницевого рівняння називають таку множину значень 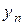 , яка задовольняє різницеве рівняння для усіх можливих значень n.
, яка задовольняє різницеве рівняння для усіх можливих значень n.
Однорідним різницевим рівнянням 1-го порядку називають рівняння виду 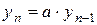 або
або 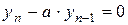 .
.
Теорема: Загальним розв’язком різницевого рівняння вигляду 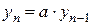 , де
, де  - задана стала, буде
- задана стала, буде 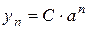 , де С – довільна стала
, де С – довільна стала
Доведення. В дане рівняння підставимо значення n = 1, 2, 3, ... Одержимо:
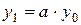 n = 1
n = 1
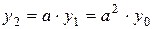 n = 2
n = 2
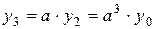 n = 3
n = 3
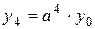 n = 4
n = 4
...
|
Порівнюючи з формулою 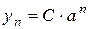 бачимо, що
бачимо, що 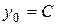 , що й потрібно було довести.
, що й потрібно було довести.
Щоб знайти частинний розв’язок різницевого рівняння, потрібно задати початкові умови.
Зауваження: Якщо 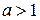 , то розв’язок
, то розв’язок 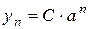 зростає за показниковим законом; якщо
зростає за показниковим законом; якщо 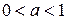 - спадає.
- спадає.
Приклад: Знайти частинний розв’язок рівняння 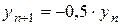 при початкових умовах
при початкових умовах 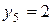
Запишемо формулу 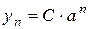 ,
,
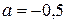
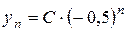 .
.
Використовуючи початкові умови знайдемо С: при n = 5 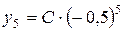
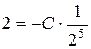
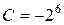
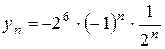
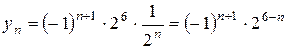
Неоднорідним різницевим рівнянням 1-го порядку називається рівняння виду
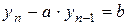 .
.
Формула для загального рівняння:
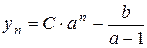 , тобто загальний розв’язок неоднорідного різницевого рівняння 1-го порядку являє собою суму двох доданків: перший – загальний розв’язок відповідного однорідного різницевого рівняння, другий – частинний розв’язок неоднорідного рівняння.
, тобто загальний розв’язок неоднорідного різницевого рівняння 1-го порядку являє собою суму двох доданків: перший – загальний розв’язок відповідного однорідного різницевого рівняння, другий – частинний розв’язок неоднорідного рівняння.
Частинний розв’язок неоднорідного різницевого рівняння знаходимо із загального розв’язку, використовуючи початкові умови.
Приклад: Розв’язати різницеве рівняння 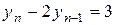 ,
,
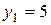
Використовуємо формулу
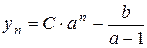
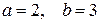
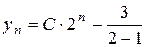
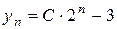 - загальний розв’язок неоднорідного різницевого рівняння.
- загальний розв’язок неоднорідного різницевого рівняння.
Знайдемо С, використовуючи початкові умови:
при n = 1, y1 = 5
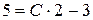
2C = 8
C = 4
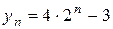 або
або 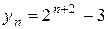
2. У фінансових розрахунках часто використовують різницеві рівняння замість геометричної прогресії.
Завдання додому
Конспект; [4] с. 66 – 71
Питання для самоконтролю
1. Однорідні лінійні різницеві рівняння.
2. Неоднорідні лінійні різницеві рівняння.
Л Е К Ц І Я 31
Тема: Числові ряди. Основні поняття.
Мета: сформувати поняття числового ряду; ознайомити із збіжними і розбіжними рядами, властивостями збіжних рядів, необхідною умовою збіжності ряду
Література: [1, с. 493-497]; [6, с. 464-473].
П Л А Н
1. Ряди. Основні значення.
2. Збіжність рядів, властивості збіжних рядів.
3. Необхідна умова збіжності
1. Нехай задано послідовність дійсних чисел u1, u2, u3, …un,…
Рядом називається вираз u1+ u2+ … +un +… 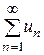 , де u1, u2, u3 - члени ряду,
, де u1, u2, u3 - члени ряду,
un – загальний член ряду.
Ряд вважається заданим, якщо його загальний член un заданий формулою,
Приклад 1: 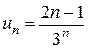
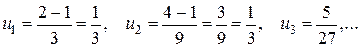
Запишемо ряд: 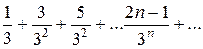
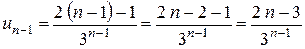
Приклад 2: Записати формулу загального члена ряду
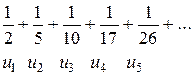
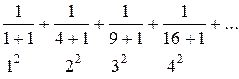
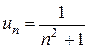
2. Нехай задано числовий ряд
u1+ u2+ u3 +… + un +…
Складемо частинні суми ряду:
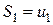
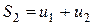
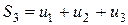
...
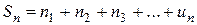
...
Одержимо послідовність частинних сум
Якщо існує границя послідовності частинних сум ряду (дорівнює якомусь значенню S), то такий ряд називається збіжним:
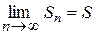 - ряд збіжний,
- ряд збіжний,
S – сума ряду.
Якщо границя послідовності частинних сум ряду не існує, то ряд називається розбіжним.