3. Неповні диференціальні рівняння.
1. Диференціальним рівнянням першого порядку називається рівняння, яке містить незалежну змінну х , невідому функцію у = у (х) та її похідну у’:
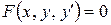 або
або 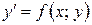
Враховуючи, що 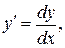 диференціальне рівняння можна записати в диференціалах:
диференціальне рівняння можна записати в диференціалах:
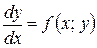
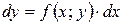
Порядок диференціального рівняння визначається по порядку старшої похідної цього рівняння:
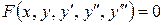 - ІІІ порядку.
- ІІІ порядку.
Розв’язком диференціального рівняння 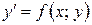 на деякому інтервалі (а; b) називається диференційована на цьому інтервалі функція
на деякому інтервалі (а; b) називається диференційована на цьому інтервалі функція 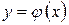 , яка при підстановці в диференціальне рівняння обертає його в тотожність.
, яка при підстановці в диференціальне рівняння обертає його в тотожність.
Графік розв’язку диференціального рівняння називається інтегральною кривою цього рівняння.
2. Теорема Коші (про існування і єдиність розв’язку)
Дано диференціальне рівняння 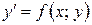 . Нехай функція
. Нехай функція 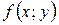 і її частинна похідна
і її частинна похідна 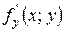 визначені і неперервні в деякій області D і нехай точка
визначені і неперервні в деякій області D і нехай точка 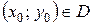 . Тоді існує єдиний розв’язок
. Тоді існує єдиний розв’язок 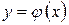 рівняння
рівняння 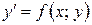 , який задовольняє умову
, який задовольняє умову 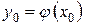 при
при 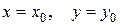 .
.
Геометрично теорема Коші стверджує, що через кожну точку області D проходить єдина інтегральна крива.
Умову 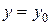 при
при 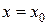 або
або 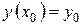 або
або 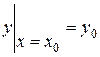 називають початковою умовою розв’язку.
називають початковою умовою розв’язку.
Умови існування і неперервності 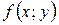 і
і 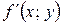 в області D називають умовами теореми Коші.
в області D називають умовами теореми Коші.
Зауваження: Точки області D, в яких не виконуються умови теореми Коші називаються особливими. Через кожну з таких точок проходить кілька інтегральних кривих або не проходить жодної.
Задача знаходження розв’язку диференціального рівняння 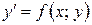 при початкових умовах
при початкових умовах 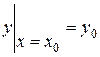 називається задачею Коші.
називається задачею Коші.
Загальним розв’язком рівняння 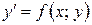 називається функція
називається функція 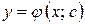 , яка залежить від змінної
, яка залежить від змінної 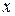 і довільної сталої С.
і довільної сталої С.
Геометрично загальний розв’язок визначає сім’ю інтегральних кривих.

 у
у
 с1
с1
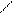
 с2
с2
с=с0
 с1
с1
 |

 0 х
0 х
Частинним розв’язком рівняння 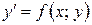 називається функція
називається функція 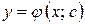 , яка знаходиться із загального розв’язку пр певному значенні сталої с=с0 .
, яка знаходиться із загального розв’язку пр певному значенні сталої с=с0 .
С0 знаходиться, використовуючи початкові умови.
Геометрично частинний розв’язок визначає одну криву із сім’ї інтегральних кривих, яка проходить через точку 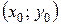 і для якої с=с0 .
і для якої с=с0 .
Загальний розв’язок називають загальним інтегралом диференціального рівняння.
Завдання додому.
1) Конспект; [1] с. 421 - 451;
[2] с. 325 – 339.
Питання для самоконтролю
1.Основні означення.
2. Задача Коші.
3. Неповні диференціальні рівняння.
Л Е К Ц І Я 28
Тема: Диференціальні рівняння першого порядку.
Мета: ознайомити з методами відокремлювання змінних, розв‘язку лінійних диференціальних рівнянь першого порядку.
Література: [1, с. 427-438]; [6, с. 438-443].
П Л А Н
1. Диференціальні рівняння з відокремлюваними змінними.








