Формула Ньютона-Лейбніца
Теорема: Якщо 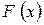 є первісною для неперервної функції
є первісною для неперервної функції 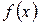 на відрізку [а; b], то справедлива формула:
на відрізку [а; b], то справедлива формула:
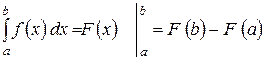
|
Приклад: 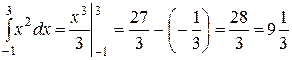
у


 у=х2 Геометрично результат дорівнює площі
у=х2 Геометрично результат дорівнює площі
криволінійної трапеції, обмеженої зверху параболою
у=х2 на відрізку [-1; 3]
 |
 -1 0 3 х
-1 0 3 х
Завдання додому
1) Конспект; [1] с. 365 – 381;
[2] с. 283 – 299
Питання для самоконтролю
1. Задачі, що приводять до поняття визначеного інтеграла.
2. Означення визначеного інтеграла та його властивості.
3. Теорема Ньютона-Лейбніца.
Л Е К Ц І Я 23
Тема: Методи обчислення визначених інтегралів.
Мета: розглянути методи обчислення визначених інтегралів.
Література: [1, с. 380-385]; [6, с. 406-416].
П Л А Н
1. Метод заміни змінної (метод підстановки);
2. Формула інтегрування частинами.
1 Метод підстановки.
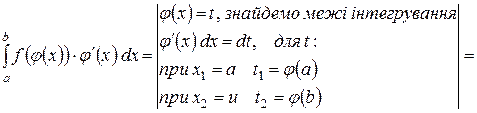
= 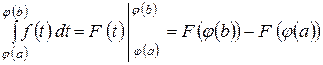
Приклад:
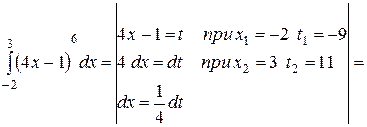
= 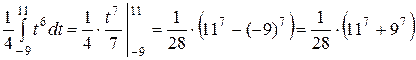
2. Формула інтегрування частинами.
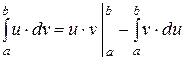
Приклад: 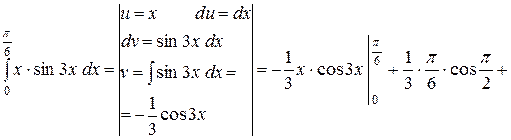
+ 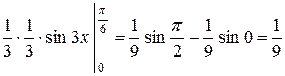
Завдання додому
1) Конспект; [1] с. 365 – 381;
[2] с. 283 – 299
Питання для самоконтролю
1. Метод заміни змінної (метод підстановки);
2. Формула інтегрування частинами.
Л Е К Ц І Я 24
Тема: Геометричне застосування визначених інтегралів.
Мета: ознайомити з обчисленням площ плоских фігур, довжиною дуги, об’ємом тіла, площею поверхні обертання.
Література: [1, с. 385- 408]; [6, с. 408-415].
П Л А Н
1. Обчислення площ плоских фігур.
2. Довжина дуги.
3. Об’єм тіла обертання.
4. Площа поверхні обертання.
 |
1. у







 у=f (x)
у=f (x)
 |
0 a b х
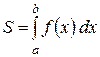
 1) 2)
1) 2)
у y






 y= f (x) y=
y= f (x) y= 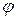 (x)
(x)


 y= f (x)
y= f (x)
 | 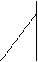 | ||||
 | |||||
 y=
y= 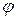 (x)
(x)
 | |||
 | |||
0 a b x 0 a c b x
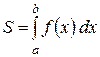
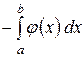
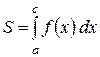
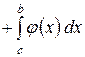
 3) 4) y a b
3) 4) y a b

 у a b
у a b




 х x
х x


 y=f (x)
y=f (x)
 |  | ||
y= 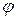 (x)
(x)
 y= f (x)
y= f (x)

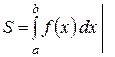
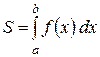
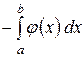
 Приклад: Обчислити площу фігури, обмеженої лініями ху=1, х=1, х=4, у=0.
Приклад: Обчислити площу фігури, обмеженої лініями ху=1, х=1, х=4, у=0.
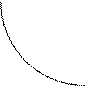 у
у
ху=1

0 1 4
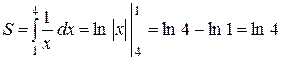 (кв. од.)
(кв. од.)
 3.
3.
у
 | |||
 | |||
a b


 0 x
0 x
 |
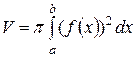 - об’єм тіла обертання навколо осі Ох .
- об’єм тіла обертання навколо осі Ох .
 |
у
d



 x=
x= 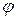 (y)
(y)
0 х
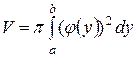 - об’єм тіла обертання навколо осі Оy .
- об’єм тіла обертання навколо осі Оy .
Приклад: Обчислити об’єм тіла обертання навколо осі Ох трапеції, обмеженої лініями 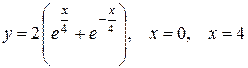
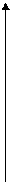 у Тіло обертання має назву катеноїд
у Тіло обертання має назву катеноїд
 |
0 4 х
 |
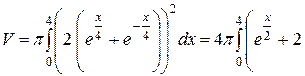
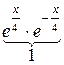
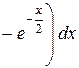 =
=
= 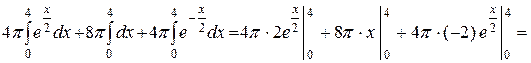
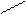
 =
= 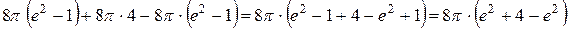 (куб. од.)
(куб. од.)
 2. у
2. у



 y= f (x)
y= f (x)
 |
0 a b х
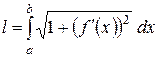
 у
у
4.
0 a b x
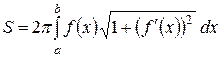
Питання для самоконтролю
1. Обчислення площ плоских фігур.
2. Довжина дуги.
3. Об’єм тіла обертання.
4. Площа поверхні обертання.
Л Е К Ц І Я 25
Тема: Невласні інтеграли.
Мета: ознайомити з нескінченними межами інтегрування (першого роду), невласного інтеграла від необмежених функцій (другого роду).
Література: [1, с. 385-394]; [6, с. 415-420].
П Л А Н
1. Невласні інтеграли з нескінченними межами інтегрування (першого роду).








