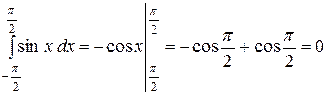2. Означення визначеного інтеграла та його властивості.
3. Теорема Ньютона-Лейбніца.
1. До поняття визначеного інтеграла приводять такі задачі:
1) про площу криволінійної трапеції;
2) про об’єм просторового тіла;
3) про роботу змінної сили;
4) про пройдений шлях та інші.
Розглянемо одну з цих задач: про площу криволінійної трапеції.
Нехай на відрізку [а; b] задано функцію 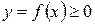
Криволінійною трапецією називається фігура, обмежена графіком даної функції у=f (x) (зверху), віссю абсцис (у=0) та відрізками прямих х=а, х=b (по боках).
 Знайдемо S ABCD
Знайдемо S ABCD

 y C Розіб’ємо відрізок [а; b] на n частинних
y C Розіб’ємо відрізок [а; b] на n частинних
 відрізків за допомогою точок
відрізків за допомогою точок
 |
 B а=х0 < x1 < x2 <… <xn = b
B а=х0 < x1 < x2 <… <xn = b
A D
 0 a x1 x2 b x
0 a x1 x2 b x
x0 xn
Позначимо довжини частинних відрізків через 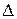 x1 =x1– x0;
x1 =x1– x0; 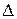 x2 =x2 – x1; ...
x2 =x2 – x1; ...
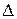 xi =xi – xi-1;
xi =xi – xi-1;
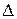 xn =xn – xn-1;
xn =xn – xn-1;
Площа і – го прямокутника
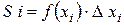
Знайдемо суму площ всіх прямокутників, одержимо площу ступінчатої фігури:
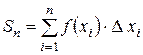
Площа ступінчатої фігури наближено дорівнює площі криволінійної трапеції
S ABCD
Спрямуємо число частинних відрізків відрізка [а; b] до нескінченності
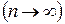 , тоді довжина кожного частинного відрізка буде прямувати до нуля (максимальна) ( max
, тоді довжина кожного частинного відрізка буде прямувати до нуля (максимальна) ( max 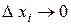 ), а площа ступінчатої фігури буде прямувати до площі трапеції, тобто:
), а площа ступінчатої фігури буде прямувати до площі трапеції, тобто:
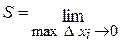
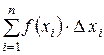 - (границя суми нескінченно великого числа
- (границя суми нескінченно великого числа
нескінченно малих доданків)
Вираз 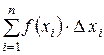 називається інтегральною сумою, а границя її (якщо вона існує)
називається інтегральною сумою, а границя її (якщо вона існує) 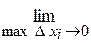 - визначеним інтегралом.
- визначеним інтегралом.
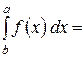
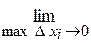
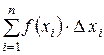
а і b – відповідно нижня і верхня межа інтегрування;
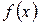 - підінтегральна функція;
- підінтегральна функція;
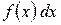 - підінтегральний вираз
- підінтегральний вираз
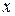 - змінна інтегрування;
- змінна інтегрування;
[а; b] – проміжок інтегрування.
Теорема 1 (достатня умова інтегрованості)
Якщо функція 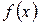 неперервна на відрізку [а; b], то вона інтегрована на цьому відрізку.
неперервна на відрізку [а; b], то вона інтегрована на цьому відрізку.
Теорема 2
Якщо функція 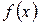 обмежена на відрізку [а; b] і неперервна в ньому скрізь, крім скінченного числа точок, в яких функція має розрив першого роду, то вона інтегрована на цьому відрізку.
обмежена на відрізку [а; b] і неперервна в ньому скрізь, крім скінченного числа точок, в яких функція має розрив першого роду, то вона інтегрована на цьому відрізку.
2. Властивості визначеного інтеграла.
1) Геометричний зміст – це площа відповідної криволінійної трапеції.
2) 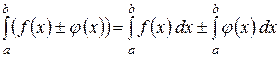
3) 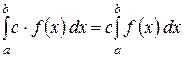
4) 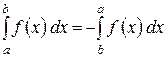
5) 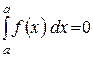
6) 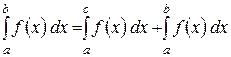 (аддитивність)
(аддитивність)
 7)
7) 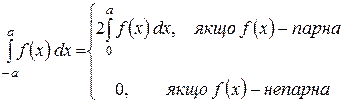
 у у
у у
 | |||
 | |||



 -а 0
-а 0
 | |||
 | |||
 -а 0 а х а х
-а 0 а х а х
Приклад: 1) 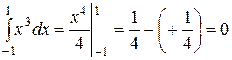
2)