Властивості невизначеного інтеграла
1) Похідна від невизначеного інтеграла дорівнює підінтегральній функції:
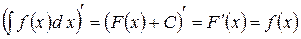
2) Невизначений інтеграл від диференціала деякої функції дорівнює сумі цієї функції і довільної сталої:
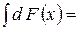
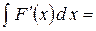
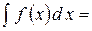
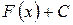
3) Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу:
|
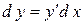
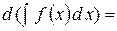
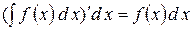
4) Сталий множник можна виносити за знак інтеграла:
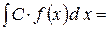
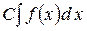, с – const
5) Невизначений інтеграл від алгебраїчної суми функцій дорівнює сумі інтегралів від цих функцій:
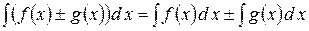
З першої властивості видно, що знаки похідної і невизначеною інтеграла взаємно знищуються. Тобто операції диференціювання та інтегрування - взаємно обернені.
Правильність виконання операції інтегрування перевіряється диференціюванням.
3. Таблиця основних інтегралів.
| 1. |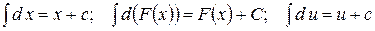 
|
| 2. |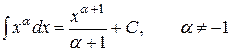 
|
| 3. |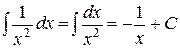 
|
| 4. |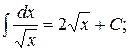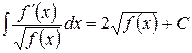  
|
| 5. |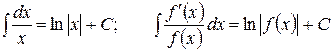 
|
| 6. |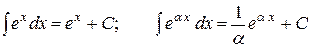 
|
| 7. |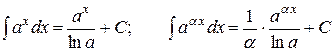 
|
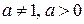
| 8. |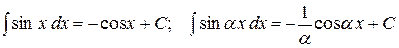 
|
| 9. |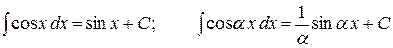 
|
| 10. |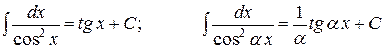 
|
| 11. |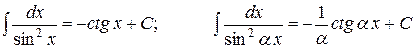 
|
| 12. |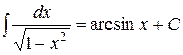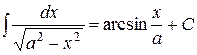  
 
|
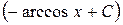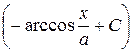
| 13. |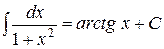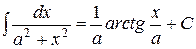  
 
|
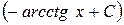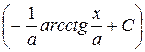
| 14. |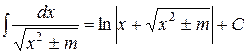 
|
| 15. |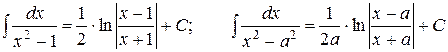 
|
| 16. |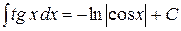 
|
| 17. |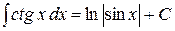 
|
| 18. |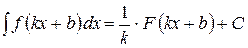 
|
Приклад. 1)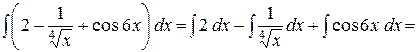 
= 
= 
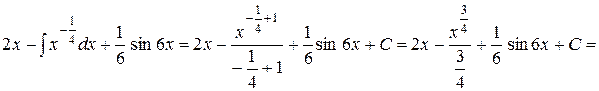
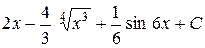
2) 
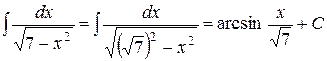
1) Нехай даний невизначений інтеграл
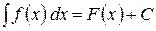
Довільна формула інтегрування залишається справедливою незалежно від того, чи змінна інтегрування є незалежною змінною, чи довільною функцією від неї, що має неперервну похідну. В цьому аклечається властивість інваріантності формули інтегрування.
Довільна формула інтегрування зберігає свій вигляд, якщо замість незалежної змінної х підставити довільну диференційовану функцію від х.
Нехай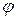 
(х) – диференційована функція:
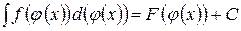
Приклад: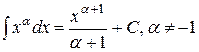 
- формула
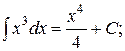
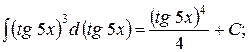
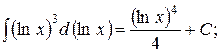
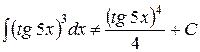
Приклад:
1) 
= 
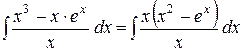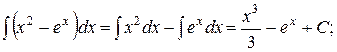
2) 
;
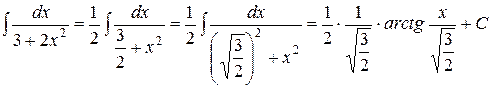3) 
= 
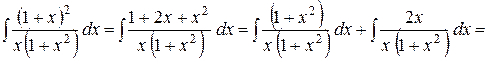
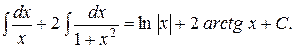
Завдання додому
1) Конспект; [1] с. 330 – 336;
[2] с. 251 – 258.
Питання для самоконтролю
1. Первісна функція.
2. Невизначений інтеграл та його властивості.
3. Таблиця основних інтегралів.
Л Е К Ц І Я 20
Тема: Основні методи інтегрування.
Мета: ознайомити з основними методами інтегрування – безпосереднього інтегрування, підстановки (заміни змінної), інтегрування частинами.
Література: [1, с. 336-342]; [6, с. 345-353].
П Л А Н
1. Метод безпосереднього інтегрування.
2. Метод підстановки (заміни змінної).
3. Метод інтегрування частинами.
1. Метод безпосереднього інтегрування.
Базується на властивостях невизначеного інтеграла і на таблиці основних інтегралів. Якщо необхідно, то виконують перетворення підінтегрального виразу.
Приклад: 1)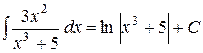 
(інтеграл №5)
2) 
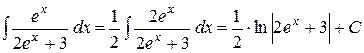
3) 
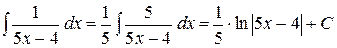
4) 
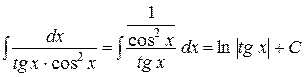
5) 
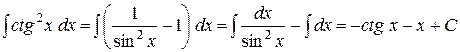
6) 
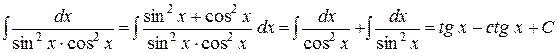
2. Метод підстановки базується на властивості інваріантності невизначеного інтеграла:
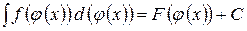
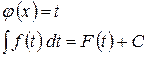
Знайдемо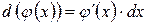 
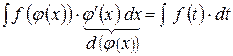
Правило. Якщо підінтегральний вираз містить похідну внутрішньої функції, то внутрішню функцію позначають новою змінною (через t):
|
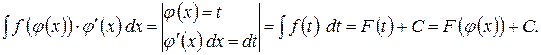
Приклад: 1)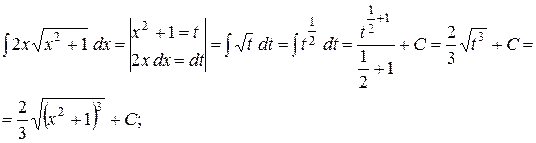 
2) 
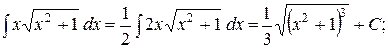
3) 
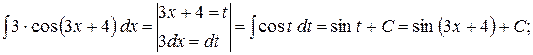
4) 
.
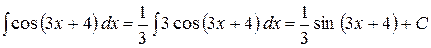3. Нехай дано дві диференційовані функції: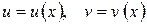 
. Знайдемо диференціал їх добутку:
|
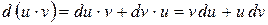
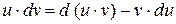
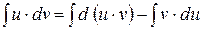
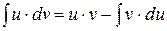