Необхідні умови існування екстремуму.
z=f (x; y), (х; у)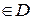 
, Р0 (х0; у0) .
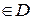Якщо в точці Р0 існує екстремум, то в цій точці частинні похідні або дорівнюють нулю, або не існують.
Точки, в яких частинні похідні дорівнюють нулю, називаються стаціонарними; точки, в яких частинні похідні дорівнюють нулю або не існують, називаються критичними.
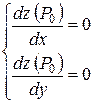
Приклад: Знайти стаціонарні точки функції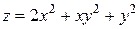 
.
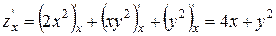
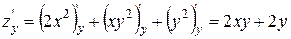
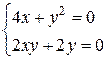
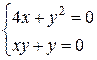
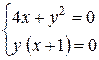
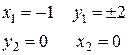
Відповідь: М1 (-1; 2), М2 (-1; -2), М3 (0; 0)
Достатні умови існування екстремуму
Нехай в точці Р0 (х0; у0) існують неперервні похідні першого та другого порядку. Позначимо А =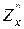 
(Р0), В= 
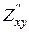(Р0), С= 
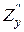(Р0). Тоді:
Якщо АС-В2<0 – екстремум існує;
А >0 (C>0) – min
A <0 (C<0) – max
Якщо АС-В2>0 – екстремум не існує;
Якщо АС-В2=0 – потрібні додаткові дослідження для визначення екстремуму.
Приклад: Знайти екстремум для попередньої функції.
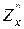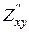=4 =2у 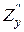= 2х + 2
1) для М1 (-1; 2) А = 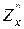(М1)=4
В = 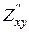(М1)=4
С= 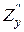(М1)=0
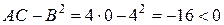- екстремуму немає
2) для М2 (-1; -2) А=4 В =-4 С=0
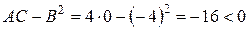- екстремуму немає
3) для М3 (0; 0) А=4 В=0 С=2
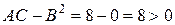- екстремум існує; так як А=4>0 - min
Zmin = (0; 0)=0
z
(0; 0; 0) у
х
2. Нехай кожній точці простору ставиться у відповідність функція, яка залежить від координат точки: u=u (х; у; z)
Значення цієї функції змінюється від точки до точки.
Тоді таке поле називається скалярним просторовим полем
Нерівномірно нагрітий камінь – це поле температур.
Задати поле – значить задати скалярну функцію в кожній точці цього поля.
Якщо поле плoське, то функція залежить від двох змінних u=u (х; у).
Означення. Нехай дано просторове поле u=u (х; у; z). Множина точок, в яких функція u=u (х; у; z) має постійне значення називається поверхнею рівного рівня поля.
u=u (х; у; z)=с, с=const.
Якщо поле плоске u=u (х; у), то лінія рівного рівня називається геометричним місцем точок, в яких функція постійна.
u=u (х; у)=с, с=const – рівняння лінії рівня.
Приклад: и=х2+у2 – поле. Скласти рівняння ліній рівня і побудувати їх.
х2+у2 =с
1) с>0, c=R2 х2+у2 =R2 -це рівняння задає множину концентричних кіл різних радіусів.
у
С3 2) с=0 х2+у2 =0 - точка
С 3) с<0, C= - R2 х2+у2 =-R2 - кола
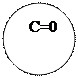уявного радіуса
х
Питання для самоконтролю
1. Похідна за напрямом.
2. Градієнт.
Л Е К Ц І Я 19
Тема: Первісна функція та невизначений інтеграл.
Мета: сформувати поняття первісної функції та невизначеного інтеграла;
ознайомити з властивостями невизначеного інтеграла, таблицею основних інтегралів, інваріантністю формули інтегрування.
Література: [1, с. 330-336]; [6, с. 337-342].
П Л А Н
1. Первісна функція.
2. Невизначений інтеграл та його властивості.
3. Таблиця основних інтегралів.
1) Розглянемо функцію f (x) на проміжку х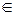 
(a; b).
Означення. Первісною для функції f (x) називається така функція F (x), похідна від якої дорівнює f (x):
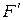(x) = f (x)
Приклад. F (x)=2х F (x) =x2
F (x) = x2 – 6
F (x) = x2+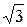 
…
З приклада можна зробити висновок, що для однієї й тієї ж функції f (x)=2х існує множина первісних, які відрізняються постійним доданком.
Теорема. Якщо F (x) – первісна функції f (x) на проміжку (a; b), то всяка інша первісна функції f (x) на цьому самому проміжку має вигляд F (x)+С.
Доведення: Нехай Ф (х) – деяка інша, крім F (x), первісна функції f (x), тобто
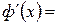f (x), х 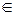(а; b). Знайдемо похідну різниці (ф (х) – F (x))’ = ф’(х) – F’(х)=
=f (x) – f (x)=0, а це означає, що ф (х) – F (x) =С, де С – сonst, тоді ф (х) = F (x) + С, що й потрібно було довести.
1) Дія знаходження множини первісних називається невизначеним інтегруванням.
Множина всіх первісних для функції називається невизначеним інтегралом, який позначається символом:
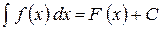, де f (x) – підінтегральна функція, f (x) d x – підінтегральний вираз, х – змінна інтегрування (знаходиться під знаком диференціала).
Невизначений інтеграл є множиною кривих, кожна з яких називається інтегральною кривою, і утворюється за допомогою паралельного переносу вздовж осі Оу .
у
F (x) + C1
F (x)
F (x) + C2
1) 
х