Достатні умови монотонності функції.
1. Якщо в кожній точці інтервалу 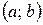 функція має додатню похідну, то в цьому інтервалі функція зростає, тобто нерівність
функція має додатню похідну, то в цьому інтервалі функція зростає, тобто нерівність 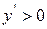 є достатньою умовою зростання функції.
є достатньою умовою зростання функції.
2. Якщо 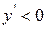 , то в інтервалі
, то в інтервалі 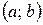 функція спадає.
функція спадає.
3. Якщо 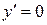 в кожній точці інтервалу
в кожній точці інтервалу 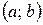 , то в цьому інтервалі функція постійна.
, то в цьому інтервалі функція постійна.
 у
у
у=с
 с
с
 0 х
0 х
 |

 y
y
у=f (x) 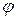 - гострий кут
- гострий кут

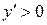
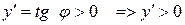
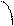
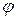
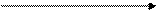 0 x
0 x
3. Розглянемо функцію у= f (x), х 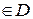 .
.
х0 – точка max, якщо значення функції в цій точці є найбільшим в порівнянні із значенням функції в деякому околі точки х0 .
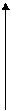 у
у

 max
max
 |  |
 0 х1 х0 х2 х
0 х1 х0 х2 х
х0 – називається точкою min, якщо значення функції в цій точці є найменшими в порівнянні із значенням функції в декому околі точки х0 .
 у
у

 min
min
 |
0 х1 х0 х2 х
Необхідна умова існування екстремума (але не достатня).
Якщо в точці х0 існує екстремум, то в цій точці похідна дорівнює 0 або не існує.
Ці точки називаються критичними (або стаціонарними).
 y Геометрично: дотична в точці
y Геометрично: дотична в точці
max екстремуму паралельна осі Ох .
 |
 min
min
 |
0 x0 x1 x
Але критичні точки не обов’язково являються точками екстремума.
Достатні умови існування екстремуму.
1) х0 є точкою екстрeмума функції y= f (x), якщо при переході через цю точку похідна змінює знак:
якщо з “+” на “ – “ – точка max;
якщо з “ – “ на “+” – точка min.
2) х0 є точкою екстремума, якщо 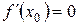 і
і 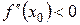 - точка max;
- точка max;
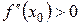 - точка min.
- точка min.
4. Загальна схема дослідження функцій та побудова графіків
І Дослідження функції y = f (x).
1) Область визначення функції, точки розриву, лівостороння і правостороння границі, вертикальні асимптоти.
2) Точки перетину графіка з осями координат.
3) Парність і непарність функції.
4) Похилі асимптоти графіка функції.
ІІ 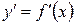
1) Знаходження точок, в яких можливий екстремум (необхідна умова).
2) Достатні умови існування екстремума.
ІІІ 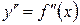
1) Знаходження точок перетину графіка (необхідні умови існування точок перетину).
2) Достатні умови існування точок перетину, інтервали опуклості і вгнутості графіка функції.
IV Поведінка функції на нескінченності, знаходження 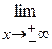 f (x).
f (x).
V Побудова графіка.
Завдання. Методами диференціального числення дослідити функцію і побудувати її графік: 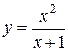
І Область визначення функції:


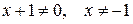
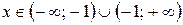 -1
-1
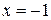 - точка розриву функції.
- точка розриву функції.
Знайдемо односторонні границі:
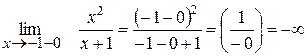
(зліва)
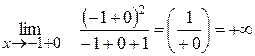
(справа)
Односторонні границі не рівні між собою і не існують, значить в точці х= -1 функція має розрив другого роду.
х =-1 – рівняння вертикальної асимптоти.

 х=-1 у Асимптота – пряма лінія, до якої
х=-1 у Асимптота – пряма лінія, до якої
наближається графік функції, але не перетинає її.
 |
-1 0 х
Асимптоти бувають вертикальні, похилі і горизонтальні.
2) З віссю Оу : при х=0 у (0)= 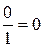 (0; 0)
(0; 0)
З віссю Ох : при у=0 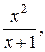
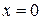 (0; 0)
(0; 0)
3) Якщо f (-x) = f (x), то функція парна (графік симетричний відносно осі Оу ).
Якщо f (-x) = -f (x), то функція непарна (графік симетричний відносно початку координат).
Якщо 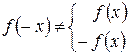 , то функція ні парна, ні непарна.
, то функція ні парна, ні непарна.
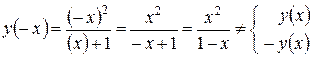 - функція ні парна, ні непарна.
- функція ні парна, ні непарна.
4) Похилі асимптоти.
Рівняння похилих асимптот шукаємо у вигляді у=kx+b,
де k -= 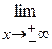
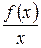 , b=
, b= 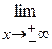
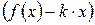 .
.
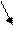
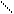
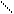 k=
k= 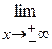
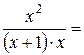
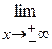
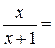
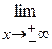
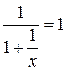
0


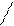 b=
b= 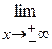
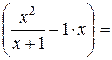
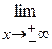
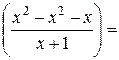
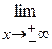
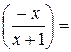
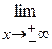
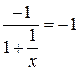
0
у=х-1 – рівняння похилої асимптоти.
 | |||
 | |||
 х=-1 у у=х-1
х=-1 у у=х-1

 -1 0 1 х
-1 0 1 х

 -1
-1
ІІ 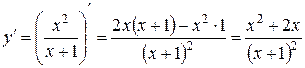
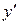 =0
=0 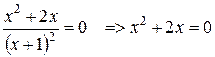
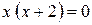
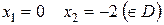
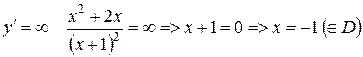




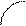
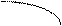 Знайдемо інтервали монотонності:
Знайдемо інтервали монотонності:



 -2 -1 0 х
-2 -1 0 х
| 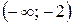
| - 2 | (- 2; -1) | ( -1; 0) | 0 | 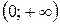
|
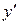
| + | 0 | - | - | 0 | + |
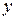
| 
| - 4 | 
| 
| 0 | 
|
max min
ІІІ 1) 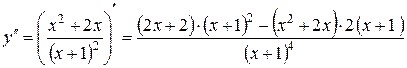 =
=

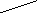

 =
= 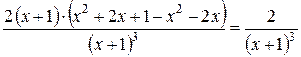
2) Точкою перетину називається точка, яка відділяє опуклу частину графіка від вгнутої.
 у
у
 А А – точка перетину
А А – точка перетину
 |
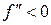
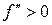
 0 х0 х
0 х0 х
Необхідні умови існування точки перетину
Якщо в точці х 0 є перегин, то в цій точці 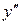 або дорівнює 0, або не існує.
або дорівнює 0, або не існує.
Якщо на деякому інтервалі 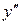 < 0, то на цьому інтервалі графік функції опуклий; якщо
< 0, то на цьому інтервалі графік функції опуклий; якщо 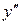 > 0 – графік функції вгнутий.
> 0 – графік функції вгнутий.
 Знайдемо точки, в яких може бути перегин:
Знайдемо точки, в яких може бути перегин: 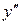 =0
=0 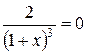 коренів немає
коренів немає 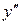 =
= 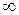
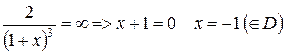
Точок перегину немає.
 3) Знайдемо інтервал опуклості і вгнутості:
3) Знайдемо інтервал опуклості і вгнутості:

 -1 х
-1 х
| х | (- 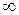 ; -1) ; -1)
| (-1; + 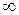 ) )
|
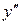
| - | + |
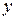
| 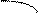  опуклий
опуклий
| вгнутий
|
IV Поведінка функції на нескінченності.


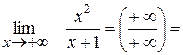
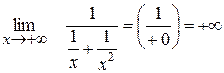
0 0
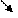
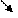
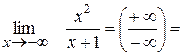
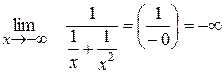
0 02
Горизонтальним асимптот функція не має (якщо k=0, то b= 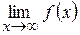 , тому у=b – рівняння горизонтальної асимптоти).
, тому у=b – рівняння горизонтальної асимптоти).
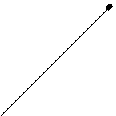
V Побудова графіка.
1) Будуємо асимптоти, точки екстремума і точки перетину, точки перетину графіка з осями координат.
2) Вітки графіка в інтервалах, де функція зростає і спадає, а також інтервали опуклості і вгнутості графіка.


 у
у


 0 х
0 х
 -1
-1
 | |||
 | |||
Завдання додому.
1) Конспект; [1] с. 265, [2] с. 212-238.
Питання для самоконтролю
1. Екстремум функції.
2. Опуклість і вгнутість кривих.
3. Асимптоти кривої.
4. Схема дослідження функції та побудова графіка.
Л Е К Ц І Я 16
Тема: Функції багатьох змінних. Частинні похідні.
Мета: Сформувати поняття функції багатьох змінних; ознайомити з границею функції z=f (x; y), частинними та повним приростами функції z=f (x; y), частинними похідними.
Література: [1, с. 284-300]; [6, с. 276-307].
П Л А Н
1. Означення функції багатьох змінних. Символіка.
2. Границя функції z=f (x; y).
3. Частинні та повний прирости функції z=f (x; y).
4. Частинні похідні.
 1. Нехай задано множину D упорядкованих пар
1. Нехай задано множину D упорядкованих пар
 y чисел (х; у).
y чисел (х; у).
y Означення. Якщо кожній парі значень (х; у) з
множини D за певним законом ставиться у відповідність
 одне значення z, то говорять, що на множині D
одне значення z, то говорять, що на множині D
0 х визначено функцію z від двох змінних х і у і записують
z=f (x; y)
Множина D є областю визначення функції z=f (x; y)
Способи задання функції:
1) символічний: z=f (x; y), z=F (x; y), z=z (x; y).
2) аналітичний: 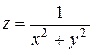 ;
;
| 3) табличний | у х | -2 | -4 | -5 | z=xy; |
| -1 | 2 | 4 | 5 | ||
| -3 | 6 | 12 | 15 | ||
| -5 | 10 | 20 | 25 |
5) графічний:
функція z=f (x; y) зображається у
z=f (x; y) вигляді поверхні, проекцією якої на



 z площину Оху є множина D
z площину Оху є множина D



 y
y


 D
D

 x
x
Побудуємо: 1) 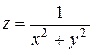
 z
z


 y
y
x
2) x2 + y2 + z2=1 – сфера
3) z=x2 +y2 - параболоїд обертання
 z
z
 |

 y
y
х
2. Означення. Число А називається границею функції z=f (x; y) при 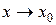 і
і
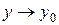 , якщо для всіх пар значень (х; у), які як завгодно мало відрізняються від (х0; у0) відповідні значення функції як завгодно мало відрізняються від числа А.
, якщо для всіх пар значень (х; у), які як завгодно мало відрізняються від (х0; у0) відповідні значення функції як завгодно мало відрізняються від числа А.
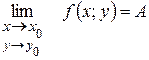
Всі властивості і правила обчислення границі такі ж, як і для границь функцій однієї змінної.
3. Розглянемо функцію z=f (x; y), х 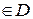 , у
, у 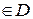 .
.
Нехай (х0; у0) – початкова точка, дамо приріст 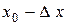 , а
, а 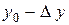 . Одержимо нову точку
. Одержимо нову точку 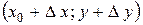 .
.
Повним приростом функції z=f (x; y) називається різниця 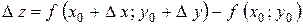 .
.
Якщо дати приріст тільки 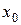 , а
, а 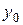 залишити без зміни, то різниця
залишити без зміни, то різниця
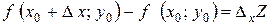 називається частинним приростом функції Z по аргументу х.
називається частинним приростом функції Z по аргументу х.
Аналогічно визначається частинний приріст функції Z по аргументу у:

4. Частинною похідною функції z по змінній х називається границя відношення частинного приросту функції по змінній х до приросту змінної х пр умові, якщо приріст аргумента х прямує до нуля.
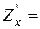 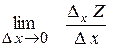
|
Аналогічно дається означення частинної похідної функції z по змінній у:
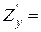 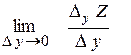
|
Частинні похідні позначаються символами:
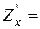 ,
, 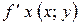 ;
; 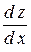 ;
; 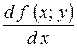
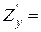 ,
, 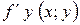 ;
; 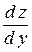 ;
; 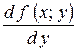
Правила знаходження частинних похідних
1) Якщо знаходиться похідна по змінній х, то у є постійною величиною.
2) Якщо знаходиться похідна по змінній у, то х є постійною величиною.
Приклад: 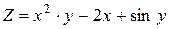
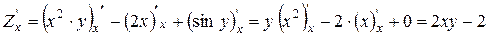
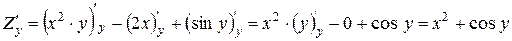
Завдання додому
1. Конспект; [1] с. 284-294
[2] с. 397-406
Питання для самоконтролю
1. Означення функції багатьох змінних. Символіка.
2. Границя функції z=f (x; y).
3. Частинні та повний прирости функції z=f (x; y).
4. Частинні похідні.
Л Е К Ц І Я 17
Тема: Похідна за напрямом. Градієнт.
Мета: сформувати поняття похідної за напрямом, градієнта, скалярного поля.
Література: [1, с. 310-318]; [6, с.297-307].
П Л А Н
1. Похідна за напрямом.
2. Градієнт.
1. Характеристиками скалярного поля є похідна за напрямом і градієнт.
Нехай дано скалярне поле u=u (х; у; z).
Частинні похідні 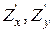 визначають швидкість зміни функції Z в напрямі осей Ох і Оу .
визначають швидкість зміни функції Z в напрямі осей Ох і Оу .
По аналогії можна знайти швидкість зміни поля в любому напрямі.
Цією швидкістю зміни поля є похідна його в певному напрямку від точки до точки.
 М1 (х1; у1; z1) Означення. Похідною функції u (х; у; z) в точці
М1 (х1; у1; z1) Означення. Похідною функції u (х; у; z) в точці
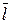 М0 (х0; у0; z0) за напрямом вектора
М0 (х0; у0; z0) за напрямом вектора 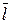 називається
називається
границя відношення приросту функції
М0 (х0; у0; z0) u (М1) – u (М0) до довжини вектора 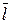 за умови,
за умови,
що М1 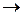 М0 , тобто
М0 , тобто 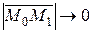
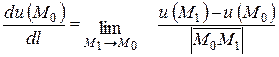
|
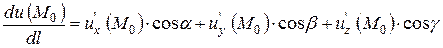
|
де 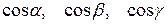 - напрямні косинуси вектора
- напрямні косинуси вектора 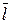
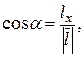
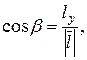
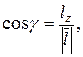
Зауваження: для плоского поля формула для обчислення 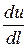 містить тільки два доданки.
містить тільки два доданки.
Величина 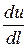 дорівнює швидкості зміни поля за напрямом вектора
дорівнює швидкості зміни поля за напрямом вектора 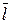 :
:
- якщо 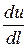 >0, то в цьому напрямі поле зростає;
>0, то в цьому напрямі поле зростає;
- якщо 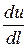 <0 – спадає;
<0 – спадає;
- якщо 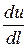 =0 – поле постійне, таке поле називається стаціонарним.
=0 – поле постійне, таке поле називається стаціонарним.
2.Нехай дано скалярне поле u=u (х; у; z).
Означення. Градієнтом функції u (х; у; z) називається вектор, координатами якого є значення частинних похідних функції u.
 grad u (х; у; z) =
grad u (х; у; z) = 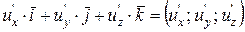
Напрям градієнта в кожній точці поля збігається з напрямом нормалі до поверхні рівня, що проходить через цю точку.

 u=c
u=c

 grad u
grad u
 |
Похідна в напрямі градієнта має найбільше значення. При цьому поле в напрямі градієнта зростає з максимальною швидкістю, а у напрямі, протилежному до напряму градієнта, найшвидше спадає.
Максимальну швидкість зміни поля можна обчислити за формулою:
max 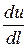 =
= 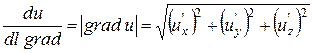
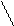
 u= grad u
u= grad u
Властивості градієнта:
1) grad (u+v)= grad u + grad v
2) grad (c 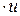 ) =
) = 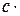 grad u
grad u
3) grad ( 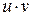 )= u grad v +v grad u
)= u grad v +v grad u
4) grad 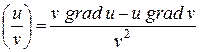
Приклад: 1. Знайти grad u в точці М (-1; 2; -2), якщо u = 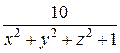
2. Знайти найбільшу швидкість зростання поля.
3. В якому напрямі функція u спадає найшвидше?
1. grad u = 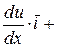
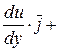
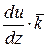
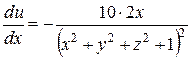 ,
, 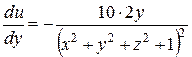
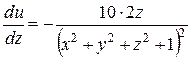
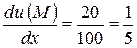
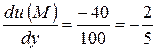 ,
, 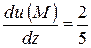
grad u= 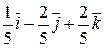
2. max 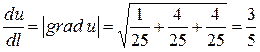
3. Напрям найшвидшого спадання поля:
- grad u= 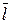
Завдання додому
1. Конспект; [2] с. 408-414.
2. Самостійна робота №11 “Метод найменших квадратів” (3 год.)
[2] с. 420-425.
3. Самостійна робота №12 “Умовний екстремум функції Z=f (x; y) в економічній
теорії» (3 год.) [2] с. 417-420
Питання для самоконтролю
1. Похідна за напрямом.
2. Градієнт.
Л Е К Ц І Я 18
Тема: Екстремум та умовний екстремум функції багатьох змінних.
Мета: сформувати поняття екстремуму та умовного екстремуму функції двох змінних.
Література: [1, с.320-327]; [6, с.313-326].
П Л А Н
1. Екстремум функції z=f (x; y). Необхідні і достатні умови існування екстремуму.
2. Поняття про скалярне поле.
1. Розглянемо функцію z=f (x; y), (х; у) 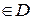 .
.
Означення. Точка Р0 (х0; у0) називається точкою max (min) функції z=f (x; y), якщо існує такий окіл точки Р0, що належить області визначення 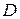 , що значення функції в довільній точці цього околу будуть меншими (більшими) значення функції в точці Р0.
, що значення функції в довільній точці цього околу будуть меншими (більшими) значення функції в точці Р0.
z max

min
 |

 y
y

 P0
P0
 х P0
х P0








