Геометричний зміст диференціала
Диференціал визначає приріст ординати дотичної, яка проведена в точці х0 до графіка функції у= f(x).
7. Інваріантність форми диференціала – незмінність: перший диференціал функції у= f(x) визначається за однією і тією самою формулою незалежно від того, чи змінна х є незалежною змінною, чи вона є функцією іншої змінної.
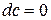
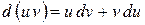
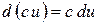
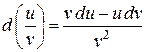
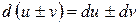
8. Диференціал функції застосовується в наближених обчисленнях.
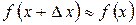
Завдання додому
1. Конспект, підготовка до практичного заняття
[1] с. 191-222
[2] с. 176-194
2. Самостійна робота №8 “Задача про неперервне нарахування відсотків”
(2 год.) [2] с. 159-161
3. Самостійна робота №9 “Поняття про еластичність функції”
(2 год.) [2] с. 196-198
Питання для самоконтролю
1. Неперервність функції у=f (x).
2. Похідна функції. Геометричний та економічний зміст.
3. Основні правила диференціювання.
4. Таблиця похідних.
5. Похідна складної функції.
6. Означення диференціала та його зміст.
7. Інваріантність форми диференціала.
8. Застосування диференціала в наближених обчисленнях.
Л Е К Ц І Я 15
Тема: Дослідження функцій. Побудова графіків.
Мета: сформувати поняття екстремума функції, опуклості і вгнутості кривих, асимптоти кривої, ознайомити з схемою дослідження функції та побудовою графіка.
Література: [1, с. 246-266]; [6, с.249-254].
П Л А Н
1. Екстремум функції.
2. Опуклість і вгнутість кривих.
3. Асимптоти кривої.
4. Схема дослідження функції та побудова графіка.
5 Видача індивідуального завдання.
1. Границя відношення двох функцій (у випадках невизначеності виду 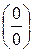 і
і 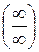 при
при 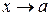 або
або 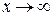 ) дорівнює границі відношення похідних цих функцій.
) дорівнює границі відношення похідних цих функцій.
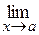
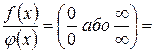
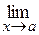
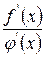
(або 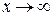 ) (або
) (або 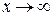 )
)
Правило Лопіталя використовується з застосуванням особливих границь і властивостей границь.
Приклад: 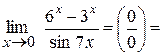
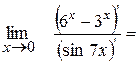
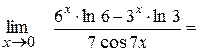
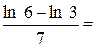
= 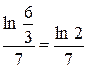
2. Розглянемо функцію у= f (x), 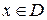 .
.
 1) Функція називається зростаючою, якщо при х2 > х1 f (x2) > f (x1).
1) Функція називається зростаючою, якщо при х2 > х1 f (x2) > f (x1).


 y
y
f (x1) f (x2)


 0 x1 x2 x
0 x1 x2 x
2) Функція називається спадною, якщо при x1 > x2 f (x2) < f (x1).
y
 | |||
 | |||
 f (x1)
f (x1)


 f (x2)
f (x2)
0 x1 x2 x
Функція, яка або тільки зростає, або тільки спадає на деякому інтервалі, називається монотонною на цьому інтервалі.








