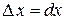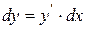2. Похідна функції. Геометричний та економічний зміст.
3. Основні правила диференціювання.
4. Таблиця похідних.
5. Похідна складної функції.
6. Означення диференціала та його зміст.
7. Інваріантність форми диференціала.
8. Застосування диференціала в наближених обчисленнях.
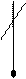 |  | ||
 1. Розглянемо у=f (x),
1. Розглянемо у=f (x),
 У х є [a; b]
У х є [a; b]



 dy х0 – початкова точка
dy х0 – початкова точка
 B у=f (x)
B у=f (x)
 Δу
Δу
 Дамо х0 приріст Δх, одержимо
Дамо х0 приріст Δх, одержимо
 A C
A C 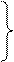


 f (x0+Δx) функцію f (x0+Δ)
f (x0+Δx) функцію f (x0+Δ)
Δx
f (x0)

 0 х0 х0+Δх х
0 х0 х0+Δх х
Різниця f (x0+Δ)-f (x0)=Δy називається приростом функції, відповідним приросту аргументу Δ х.
Означення. Функція у=f (х) називається неперервною в точці х0, якщо ця функція визначена в деякому околі точці х0 і якщо 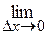 Δу=0, тобто нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції.
Δу=0, тобто нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції.
Якщо границя приросту функції при 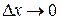 не дорівнює 0, то функція в точці х0 має розрив.
не дорівнює 0, то функція в точці х0 має розрив.
 у
у
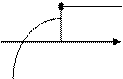
х0 х
1. Означення. Функція у=f (х) називається неперервною на деякому проміжку
[ 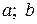 ], якщо вона неперервна в кожній точці цього проміжку.
], якщо вона неперервна в кожній точці цього проміжку.
2. Означення. Похідною функції у=f (х) називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.
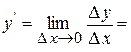
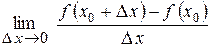
Похідна позначається символами:
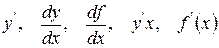 .
.
Геометричний зміст похідної:
З Δ АВС: 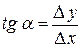
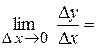
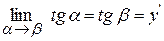
Похідна визначає тангенс кута нахилу дотичної до осі абсцис в початковій точці х0 .
Економічний зміст похідної:
Продуктивність праці є похідною об’єму продукції за часом.
Похідна визначає швидкість зміни функції точці.
Операція знаходження похідної від функції y=f (x) називається диференціюванням цієї функції.
Нехай функція u=u (x) та v=v (x) – неперервні.
1) 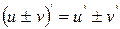
2) 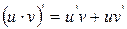
3) 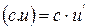 с – const
с – const
4) 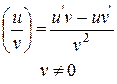
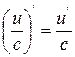 с – const
с – const
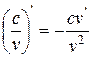 c – сonst
c – сonst
4. Таблиця похідних
| 1. | с’=0, с – const | |
| 2. | х’=1 | |
| 3. | 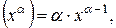 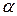 - довільне число - довільне число
| 3. 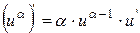
|
| 4. | 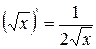
| 4. 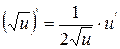
|
| 5. | 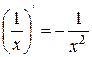
| 5. 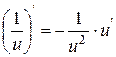
|
| 6. | 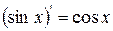
| 6. 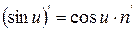
|
| 7. | 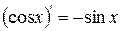
| 7. 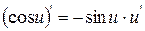
|
| 8. | 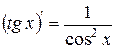
| 8. 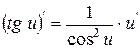
|
| 9. | 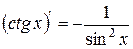
| 9. 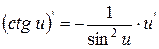
|
| 10. | 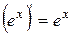
| 10. 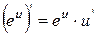
|
| 11. | 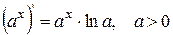
| 11. 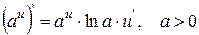
|
| 12. | 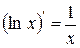
| 12. 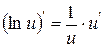
|
| 13. | 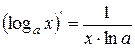
| 13. 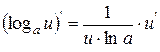
|
| 14. | 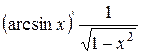
| 14. 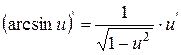
|
| 15. | 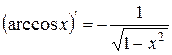
| 15. 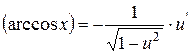
|
| 16. | 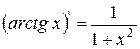
| 16. 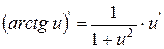
|
| 17. | 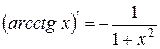
| 17. 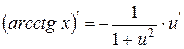
|
Приклад: 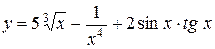
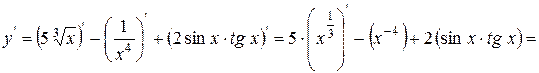
= 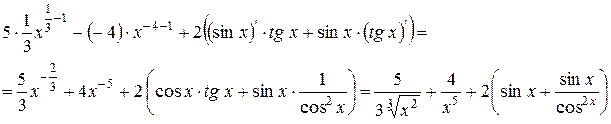
5. Нехай дана складна функція у=f (g (x) ).
Щоб знайти похідну складної функції потрібно похідну від зовнішньої функції помножити на похідну від внутрішньої функції.
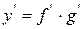 Приклади:
Приклади:
1) 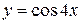
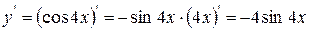
2) 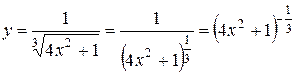
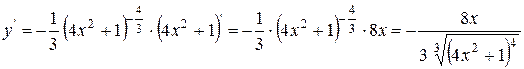
6. у= f(x), х є D, 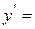
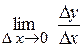
За властивістю границі маємо:
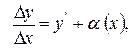 де
де 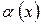 - нескінченно мала;
- нескінченно мала;
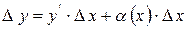
Доданок 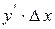 називається головною частиною приросту функції, її ще називають диференціалом функції:
називається головною частиною приросту функції, її ще називають диференціалом функції:
|
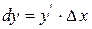
|
Приріст незалежного аргумента дорівнює його диференціалу , тоді формулою диференціал можна записати так: