Властивості границь
1)  (f (x)+g (x)) =
(f (x)+g (x)) =  f (x) +
f (x) +  g (x)
g (x)
(якщо =  f (x) і
f (x) і  g (x) існують)
g (x) існують)
для всіх властивостей
2)  (f (x)
(f (x) 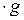 (x)) =
(x)) =  f
f 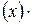
 g (x)
g (x)
3) 
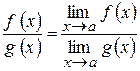 , якщо
, якщо  g (x)
g (x) 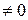
4)  c
c 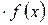 =
= 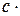
 f (x), де с – const
f (x), де с – const
5)  С=С, де С –const
С=С, де С –const
6) Для того, щоб число А було границею функції f (x) при 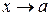 , необхідно і достатньо, щоб різниця f (x) – А була нескінченно малою величиною, тобто
, необхідно і достатньо, щоб різниця f (x) – А була нескінченно малою величиною, тобто
 f (x) =A <=>
f (x) =A <=> 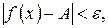
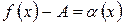
де 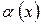 - нескінченно мала величина;
- нескінченно мала величина;
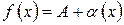
| Тобто функція мало відрізняється від своєї границі на |
нескінченно малий доданок: 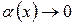 при
при 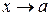
Односторонні границі
1) Лівостороння границя
Границя функції при 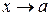 за умови, що х залишається меншим за
за умови, що х залишається меншим за  , називається лівосторонньою.
, називається лівосторонньою.


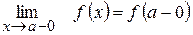
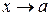 х
х
2) Правостороння границя
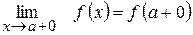

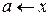 х
х
Приклад: 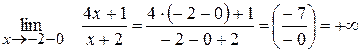
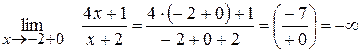
Одна з ознак існування границі (про границю проміжної функції)
Нехай функції 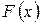 і Ф (х) при
і Ф (х) при 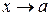 мають одну й ту ж границю:
мають одну й ту ж границю:
 F (x) =
F (x) =  Ф (х) =А. Нехай функція f (x) задовольняє нерівність
Ф (х) =А. Нехай функція f (x) задовольняє нерівність
F (x) 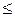 f (x)
f (x) 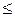 Ф (х). Перейдемо до lim при
Ф (х). Перейдемо до lim при 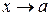 :
:
 F (x)
F (x) 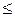
 f (x)
f (x) 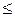
 Ф (х)
Ф (х)
А 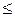
 f (x)
f (x)  A
A
 f (x) =A
f (x) =A
Завдання додому
1. Конспект, підготовка до практичного заняття
2. Самостійна робота №5 “Графіки елементарних функцій” (2 год.)
[1] c. 138-142
3. Самостійна робота №6 “Границя послідовності” (2 год.)
[1] с. 149-153
4. Самостійна робота №7 “Порівняння нескінченно малих і нескінченно великих величин” (2 год.)
[2] с. 147-153
Питання для самоконтролю
1. Означення функції, способи її задання.
2. Границя змінної величини.
3. Нескінченно малі і нескінченно великі величини, їх зв’язок.
4. Границя функції. Односторонні границі.
Л Е К Ц І Я 13
Тема: Особливі границі
Мета: Ознайомити з першою та другою особливими границями, натуральними логарифмами, порівнянням нескінченно малих
Література: [1, с. 169-183]; [6, с. 212-216].
П Л А Н
1. Перша особлива границя 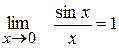
2. Друга особлива границя 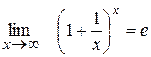
3. Натуральні логарифми.
4. Порівняння нескінченно малих.
1. Нехай дано круг радіуса R
 У Радіанна міра
У Радіанна міра  АОВ
АОВ 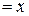 ,
,
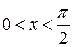 (
( 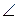 АОВ утворений радіусом
АОВ утворений радіусом
 круга і віссю Ох).
круга і віссю Ох).



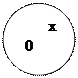 А АС –дотична до кола в т.А
А АС –дотична до кола в т.А
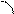 |

 В С х
В С х
Порівнюючи площі 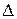 АОВ, сектора круга АОВ і
АОВ, сектора круга АОВ і 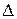 АОС, дістанемо:
АОС, дістанемо:
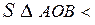
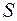 сект АОВ < S
сект АОВ < S 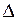 АОС;
АОС;
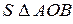 =
= 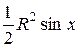 , S сект АОВ =
, S сект АОВ = 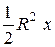 ,
,
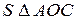 =
= 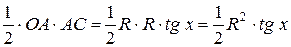 ;
;
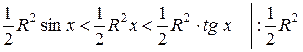
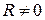
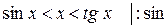
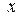
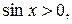 так як
так як 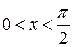
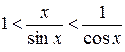
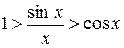
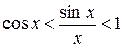
Перейдемо до границі при 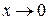 ;
;
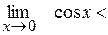

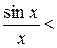
 1;
1;
1< 
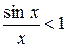 , звідки
, звідки
 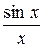 =1 =1
| - перша особлива границя |
Для першої особливої границі невизначеність 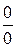
Приклади: 1) 
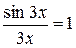 2)
2) 
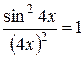
Для обчислення першої особливої границі застосовують формули тригонометрії (для перетворення виразів):
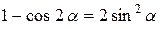 ;
; 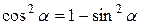
 1
1


 Приклад:
Приклад: 
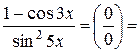

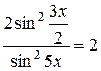

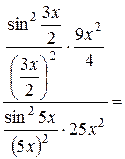
1
= 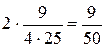
Наслідки першої особливої границі:
1) 
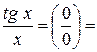

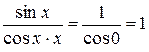
2) 
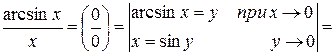

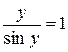
3) 
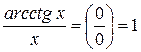
3) Розглянемо множину логарифмичних кривих при умові, коли основа логарифма більша за 1: у=log a x, a>1, x>0
у y=log a x (а>1) Нехай до кожної кривої
 проведена дотична в точці х=1
проведена дотична в точці х=1
Серед цих кривих знайдеться
 така, дотична до якої в т.х=1
така, дотична до якої в т.х=1
 нахилена до осі Ох під кутом 450
нахилена до осі Ох під кутом 450
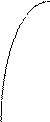
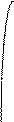

 0 1 x
0 1 x
Основою логарифма такої кривої є число е, значення його знаходиться в межах 2 < e < 3.
е=2,7182818284... е 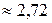 - ірраціональне.
- ірраціональне.
Число е називається числом Непера (на честь шотландського математика Дж. Непера – винахідника логарифмів) або числом Ейлера. Число е трансцендентне (тобто не є коренем алгебраїчного рівняння з цілими коефіцієнтами).
Логарифми за основою е називаються натуральними і позначаються ln x. Натуральні логарифми мають такі ж властивості, як і логарифми за любою основою:
1) ln 1 =0 7) lg 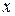 =
= 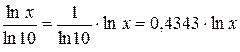
2) ln e =1
3) ln 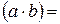 ln
ln 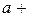 ln
ln 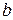
4) ln 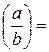 ln
ln  -ln
-ln 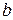
5) ln 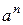 =
= 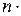 ln
ln 
6) ln 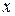 =
= 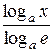


 Число
Число 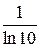 називається модулем переходу від десяткового логарифма до натурального.
називається модулем переходу від десяткового логарифма до натурального.
у y=ln x Побудуємо графік функції у=ln x
В АВ – пряма, яка перетинає

 графік функції у=ln x в двох
графік функції у=ln x в двох
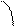 А 450
А 450 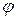 ln (1+
ln (1+ 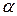 ) точках (січна).
) точках (січна).

 0 С х
0 С х
1 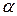
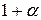
Нехай 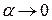 , тоді т. В, переміщаючись по кривій, прямує до т. А (
, тоді т. В, переміщаючись по кривій, прямує до т. А ( 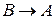 ). Січна АВ займе положення дотичної, проведеної в т.А в деякий момент. При цьому кут нахилу до осі Ох буде дорівнювати 450 (
). Січна АВ займе положення дотичної, проведеної в т.А в деякий момент. При цьому кут нахилу до осі Ох буде дорівнювати 450 ( 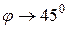 ).
).
З 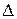 АВС знайдемо
АВС знайдемо 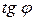 :
: 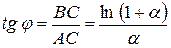 .
.
Знайдемо 
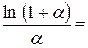
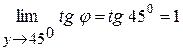

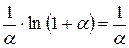

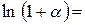

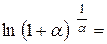 ln
ln 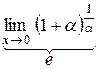 =1
=1
Зауваження: 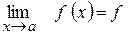 (
( 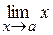 ) за властивістю границі, якщо функція неперервна, то можна поміняти місцями символи lim і f.
) за властивістю границі, якщо функція неперервна, то можна поміняти місцями символи lim і f.
(границі) (функції)
| Значить, |  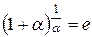
| - друга особлива границя |
Для другої особливої границі невизначеність 1 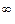
Другий запис другої особливої границі:
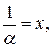
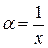 ;
;
при 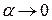
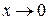
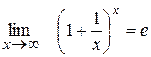
|
Приклад: 1) 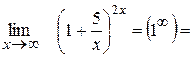
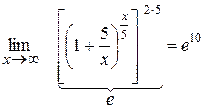
2) 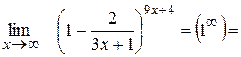
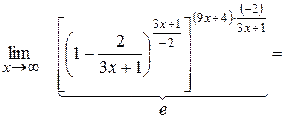
 0
0
 =
= 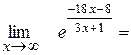
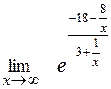 =
= 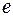
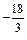 =
= 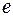 -6 =
-6 = 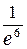
0
4. Дві нескінченно малі порівнюються між собою за допомогою дослідження їхнього відношення.
Нехай дано дві нескінченно малі:
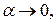
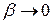
1) 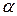 і
і 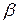 називаються нескінченно малими одного порядку, якщо
називаються нескінченно малими одного порядку, якщо
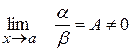 , А є R.
, А є R.
2) 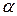 називається нескінченно малою вищого порядку, ніж
називається нескінченно малою вищого порядку, ніж 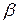 , якщо
, якщо 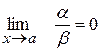 .
.
3) 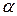 називається нескінченно малою нижчого порядку, ніж
називається нескінченно малою нижчого порядку, ніж 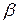 , якщо
, якщо 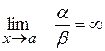 .
.
4) Якщо 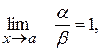 то
то 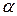 і
і 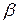 - еквівалентні нескінченно малі
- еквівалентні нескінченно малі 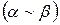 .
.
Теорема про заміну відношення нескінченно малих відношенням еквівалентних величин: при знаходженні границі відношення нескінченно малих можна замінити їх еквівалентними величинами
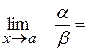
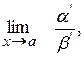 де
де 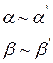
Еквівалентність деяких нескінченно малих (при 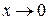 ):
):
sin x ~ x, tg x ~ x, arcsin x ~ x,
arctg x ~ x, sinkx ~xk


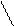 Приклад:
Приклад: 
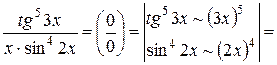

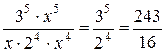
Завдання додому
1. Конспект, підготовка до практичного заняття.
Питання для самоконтролю
1. Перша особлива границя 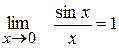
2. Друга особлива границя 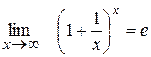
3. Натуральні логарифми.
4. Порівняння нескінченно малих.
Л Е К Ц І Я 14
Тема: Неперервність функції. Похідна. Диференціал функції у= f(x).
Мета: сформувати поняття неперервності функції; ознайомити з похідною, її метричним та економічним змістом, основними правилами диференціювання, таблицею похідних, похідною складної функції.
Література: [1, с. 191-222]; [6, с. 237-260].
П Л А Н
1. Неперервність функції у=f (x).








