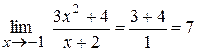Нескінченно малі величини
Нехай змінна величина* х в деякому процесі нескінченно зменшуючись наближається до 0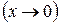 
, тоді говорять, що х є нескінченно малою величиною.
* Величина, границя якої дорівнює 0
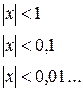
Означення. Змінна величина х називається нескінченно малою в процесі її зміни, якщо існує яке завгодно мале додатнє число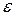 
, таке, що починаючи з деякого значення, всі наступні значення х задовольняють нерівність 
.
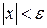Тобто значення х попадає в 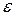- окіл нуля.
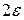
х х
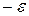0
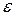
Властивості нескінченно малих величин
1) Сума (різниця) нескінченно малих величин є величина нескінченно мала.
2) Добуток нескінченно малих величин є величина нескінченно мала.
3) Частка від ділення нескінченно малої величини на функцію, яка має відмінну від нуля границю, є величина нескінченно мала.
4) Добуток обмеженої функції на нескінченно малу є величина нескінченно мала.
5) 
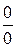-невизначеність.
Нескінченно великі величини.
Означення. Змінна величина х називається нескінченно великою в деякому процесі, якщо для довільного як завгодно великого додатнього числа М її модуль більший від М: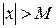 
.
Говорять, що змінна х прямує до нескінченності і пишуть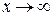 
або lim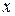 
= 
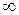
Нескінченно великі величини можуть бути і від’ємними, і додатніми.
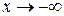- нескінченно велика від’ємна величина
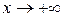- нескінченно велика додатня величина
Властивості нескінченно великих величин
1) 
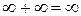
2) 
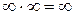
3) 
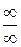- невизначеність
4) 
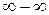- невизначеність
Зв’язок між нескінченно великими і нескінченно малими величинами
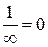Величина, обернена нескінченно великій, є нескінченно мала
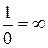Величина, обернена нескінченно малій, є нескінченно велика
3. Нехай дана функція у=f (х). Число А називається границею функції f (х) при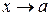 
, якщо для всіх значень х, які як завгодно мало відрізняються від 
, відповідні значення у як завгодно мало відрізняються від А.
f(x)=А
 |
у у= f(x) Означення
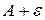Число А називається границею
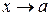А функції у= f(x) при , якщо для
будь-якого наперед заданого скільки
А- 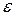завгодно малого числа 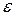>0
знайдеться таке число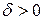 
, що для
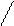будь-якого х, відмінного від , при
0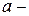 
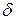
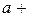
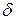х виконанні нерівності 
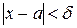виконується нерівність 
.
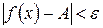Якщо значення х попадає в 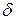-окіл точки , то значення у попадає в
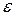-окіл точки А.
Правило обчислення границі
f (x) = f (a), якщо f (a) існує.
Приклад: Знайти 