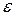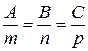2. Взаємне розташування площин.
3. Рівняння прямої в R3 .
4. Взаємне розташування прямих, прямої та площини.
5 Аналітична геометрія в економіці.
1. Рівняння площини в просторі містить змінні х, у та z в першому степені
Розглянемо, який вид має рівняння площини. Нехай М1 (х1; у1; z1) –фіксована точка площини, М (х; у; z) – довільна точка площини (змінна)
 z
z
 |




 0 y
0 y
 |
 x
x
 Заданий вектор
Заданий вектор 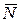 = (А; В; С;)
= (А; В; С;)
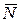 = (А; В; С;) перпендикулярний площині. Він називається
= (А; В; С;) перпендикулярний площині. Він називається
 нормальним вектором площини.
нормальним вектором площини.
 М (х; у; z)
М (х; у; z)
М1 (х1; у1; z1)
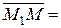 (х-х1; у-у1; z-z1)
(х-х1; у-у1; z-z1)
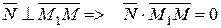
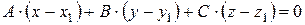
| Рівняння площини, яка проходить через задану т. М1 |
Загальне рівняння площини
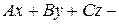
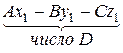
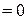
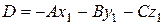
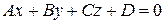
| 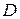 - вільний член - вільний член
|
Для того, щоб побудувати площину в системі координат, потрібно знайти точки перетину її з осями координат.
Приклад: Побудувати площину 3х-у+2z-6=0
 |
Z 1) при х=0, у=0 2z=6
z=3
2) при х=0, z=0 3x=6


 - 3 x=2
- 3 x=2

 -6 - 0
-6 - 0


 | | | y 3) при x=0, z=0 –y=-6
| | | y 3) при x=0, z=0 –y=-6
 2 y=-6
2 y=-6
x
Дослідження загального рівняння площини.

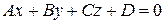 z
z
 |
 1)
1) 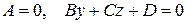



 площина | | Ох 0 у
площина | | Ох 0 у
 x
x
 |
z
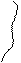


 2)
2) 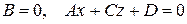


 площина | | Оy
площина | | Оy

 0 y
0 y
x
 3)
3) 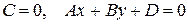 z
z
площина | | Оz
 |



 0
0
y
 |
x
4) 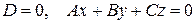 z
z
 площина проходить через початок координат
площина проходить через початок координат
 |

 y
y
x
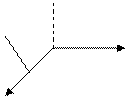
5) 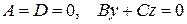
 площина проходить через вісь Ох
площина проходить через вісь Ох

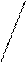 z
z
 |
0 y
x
6) 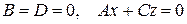
 площина проходить через вісь Оу
площина проходить через вісь Оу
z
 |

 0 y
0 y
x
7) 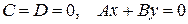
площина проходить через вісь Оz
 z
z
 |
0


 y
y
8) x
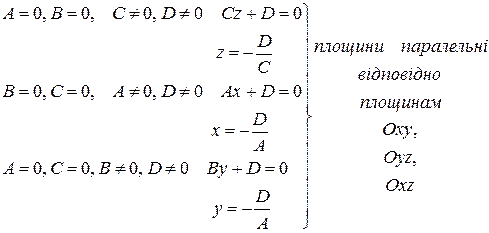
9)
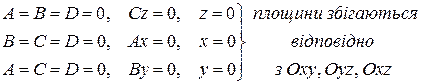
Рівняння площини у відрізках на осях.
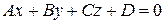
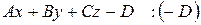
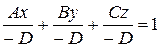
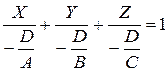
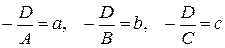
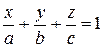
| 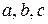 -відрізки, які відтинає площина на осях Ох, Оу, Оz
відповідно -відрізки, які відтинає площина на осях Ох, Оу, Оz
відповідно
|
 z
z

 с
с


 у
у

 х
х

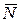 1=(А1; В1; С1)
1=(А1; В1; С1)
 1) Площини можуть бути паралельними.
1) Площини можуть бути паралельними.
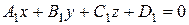
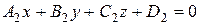

 2=(А2; В2; С2)
2=(А2; В2; С2)
 |
Якщо площини паралельні, то їх нормальні вектори колінеарні.
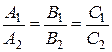
| - умова паралельності площин |
2) Площини можуть бути перпендикулярними.
 |

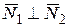

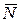 2
2
 |
 1
1
 |
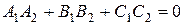
| - умова перпендикулярності площин |
3) Кут між площинами обчислюється як косинус кута між 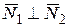
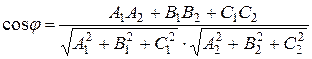
4) Відстань від точки до площини.
 М0 (х0; у0; z0) Ах+Ву+Сz+D=0 - площина
М0 (х0; у0; z0) Ах+Ву+Сz+D=0 - площина
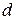

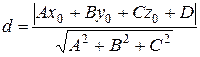
3. Довільна пряма в просторі розглядається як пряма перетину двох площин, тому рівняння прямої в загальному вигляді задається як система рівнянь площин: 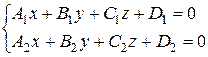
Канонічне рівняння прямої.
 =(m; n; p)
=(m; n; p)
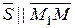
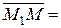 (х-х1; у-у1; z-z1)
(х-х1; у-у1; z-z1)
М1 (х1; у1; z1) М (х; у; z)

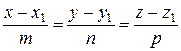
|
Рівняння прямої, яка проходить через дві задані точки.
М1 (х1; у1; z1) М2 (х2; у2; z2)
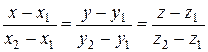
|
4. Взаємне розташування прямих.
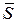

 1 (1) (2)
1 (1) (2) 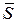

 1 =(m1; n1; p1),
1 =(m1; n1; p1), 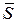 2 =(m2; n2; p2)
2 =(m2; n2; p2)
 Якщо прямі паралельні, то їх
Якщо прямі паралельні, то їх
напрямні вектори колінеарні

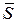 2
2
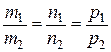
| - умова паралельності прямих |
Перпендикулярні.


 (1)
(1) 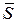 2 (2)
2 (2)

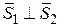
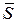 1
1
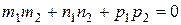
| - умова перпендикулярності прямих |
3) Кут між двома прямими дорівнює куту між їхніми напрямними векторами 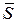 1 і
1 і 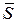 2 .
2 .
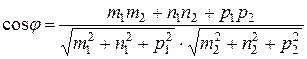
Взаємне розташування прямої та площини.
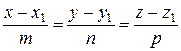 - пряма
- пряма
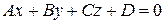 - площина
- площина
1) Паралельні.
 |
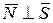
|


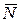 - умова паралельності
- умова паралельності
 прямої і площини
прямої і площини
2) Перпендикулярні. 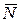 ||
|| 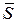

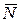
|


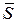

 - умова перпендикулярності
- умова перпендикулярності
прямої і площини

Завдання додому
1. Конспект, підготовка до практичного заняття.
2. [1] с. 84-93
Питання для самоконтролю
1. Рівняння площини в R3 .
2. Взаємне розташування площин.
3. Рівняння прямої в R3 .
4. Взаємне розташування прямих, прямої та площини.
5 Аналітична геометрія в економіці.
Л Е К Ц І Я 12
Тема: Функція однієї змінної. Границя функції
Мета: сформувати поняття функції, розглянути способи її задання; ознайомити границею змінної величини, нескінченно малими і нескінченно великими величинами, зв’язком між ними, границею функції, односторонніми границями.
Література: [1, с. 148-164]; [6, с. 205-218].
П Л А Н
1. Означення функції, способи її задання.
2. Границя змінної величини. Нескінченно малі і нескінченно великі величини, їх зв’язок.
3. Границя функції. Односторонні границі.
1. Якщо кожному елементу х з деякої множини Х за певним правилом ставиться у відповідність єдиний елемент у з множини У, то говорять, що у є функція від х і пишуть у=f (x).*
*Це означення належить М.І.Лобачевскому і Л.Діріхле.
х – незалежна змінна (або аргумент).
у – залежна змінна (або значення функції).
Множина Х називається областю визначення функції, множина У – область значень.
Способи задання функції.
1) Аналітичний (за допомогою формули).
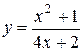
при 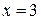
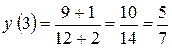
2) Графічний (за допомогою графіка).
 |
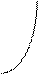
 у
у
у=х2
 0 х
0 х
3) Табличний
| х | -2 | -1 | 0 | 1 | 2 |
| у | -8 | -1 | 0 | 1 | 8 |
4) Словесний
Функція Діріхле: f (x)=1, якщо х – раціональне число; f (x)=0, якщо х – ірраціональне число.
2. Нехай в деякому процесі змінна величина х наближається до числа  , тоді говорять, що х прямує до
, тоді говорять, що х прямує до  і пишуть
і пишуть 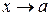 . Це значить, що починаючи з деякого значення, х приймає як завгодно близькі до числа
. Це значить, що починаючи з деякого значення, х приймає як завгодно близькі до числа  значення, але не рівні
значення, але не рівні  . Тоді говорять, що число
. Тоді говорять, що число  є границею змінної величини х, і пишуть
є границею змінної величини х, і пишуть
 =
= 
Означення Число  називається границею змінної величини х, якщо для довільного числа
називається границею змінної величини х, якщо для довільного числа 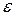 >0, починаючи з деякого значення, всі наступні значення х задовольняють нерівність
>0, починаючи з деякого значення, всі наступні значення х задовольняють нерівність 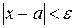 .
.
Тобто, починаючи з деякого значення, всі наступні значення х попадають
в 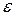 - окіл точки
- окіл точки  і в процесі зміни залишаються в цьому околі.
і в процесі зміни залишаються в цьому околі.
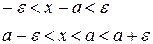
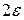
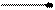
0 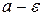

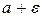 х
х