Дослідження загального рівняння прямої
а) Нехай А=0, Ву+С=0 – пряма, паралельна осі Ох
 |
у
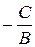



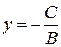
0 х
б) Нехай В=0, Ах+С=0 – пряма, паралельна осі Оу

 у
у


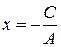
0 х
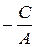
в) С=0, Ах+Ву=0 – пряма, проходить через початок координат
 |
 у
у

 0 х
0 х
6) Рівняння прямої у відрізках на осях.
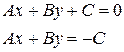
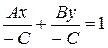
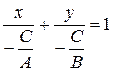
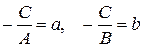
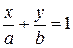
| Рівняння прямої у відрізках на осях |

 у
у  і
і 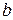 - відрізки, які
- відрізки, які
 віднімає пряма на осях Ох та Оу
віднімає пряма на осях Ох та Оу
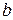

 0
0  х
х
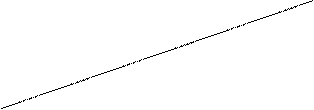
2. Нехай дані рівняння двох прямих: 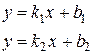

 у
у
 |

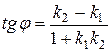
0 х
Якщо рівняння прямих задані в загальному вигляді Ах+Ву+С=0, то
| Кутовий коефіцієнт | 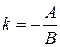
|
Умова паралельності прямих
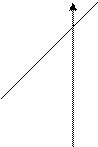 |
 у
у
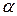 1
1 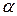 2
2
 0 х
0 х
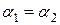 , значить
, значить
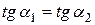
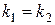
|
Умова перпендикулярності прямих
 1
1
 |
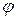 900
900
 2
2
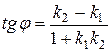
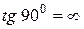 ( не існує)
( не існує)
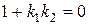
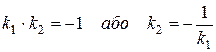
|
3.
 М0 (х0; у0) Нехай пряма задана рівнянням
М0 (х0; у0) Нехай пряма задана рівнянням
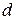 Ах+Ву+С=0
Ах+Ву+С=0
 |
М0 (х0; у0) – точка, яка не лежить на цій прямій.
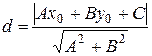
Приклади:
1) Записати рівняння прямої, яка проходить через точку М (-1; 2) перпендикулярно прямій 2х-у+1=0
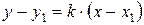
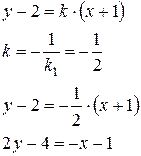
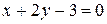
2) Загальне рівняння прямої записати у відрізках на осях і побудувати пряму:
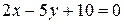
 y
y
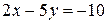


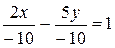 2
2







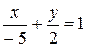 -5 0 x
-5 0 x
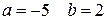
3) Записати рівняння прямої, яка проходить через точки М1 (-2; 5), М2 (3; 5)
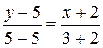
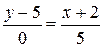
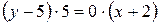
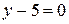 - пряма, паралельна осі Ох
- пряма, паралельна осі Ох
Додатково: Побудова система нерівностей.
Довільна пряма ділить площину на дві півплощини Ах+Ву+С=0
 у Ах+Ву+С
у Ах+Ву+С 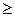 або Ах+Ву+С
або Ах+Ву+С 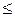 0 – ці нерівності,
0 – ці нерівності,
 описують множину точок, які належать
описують множину точок, які належать
одній із півплощин
 |
0 х
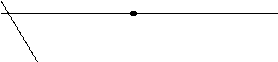
Для того, щоб побудувати шукану півплощину , потрібно:
1) побудувати пряму Ах+Ву+С=0;
2) з довільної півплощини вибрати точку з відомими координатами і ці координати підставити в нерівність. Якщо зміст нерівності зберігся, то нерівність описує ту півплощину, з якої була вибрана точка. Якщо зміст нерівності не зберігся, то нерівність описує другу півплощину.
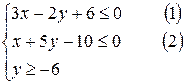
у
 | |||
 | |||

 3
3

 2
2
 -2
-2











 0 10 х
0 10 х
 |  | ||
-5
 |
Завдання додому
1) Конспект; [1] с. 76-83
Питання для самоконтролю
1. Різні види рівнянь прямої на площині.
2. Кут між двома прямими.
3. Відстань від точки до прямої.
Л Е К Ц І Я 11
Тема: Площина та пряма в трьохвимірному просторі R3
Мета: ознайомити з рівнянням площини в R3, рівнянням прямої в R3 , розглянути взаємне розташування площин, прямих, прямої та площини.
Література: [1, с. 84-96]; [6, с. 167-179].
П Л А Н
1. Рівняння площини в R3 .








