Розклад вектора за даним базисом
Нехай дана система n векторів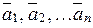 
. Потрібно перевірити, чи утворює дана система базис, і розкласти вектор 
за даним базисом.
1) Вектор подамо у вигляді лінійної комбінації векторів 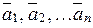; коефіцієнти лінійної комбінації являються координатами , який потрібно знайти, тому позначимо їх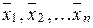 
:
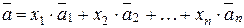(1)
2) В рівності (1) замість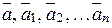 
запишемо стовпці їх координат.
3) Виконавши дії над одержаною рівністю у вигляді матриць, одержимо систему n рівнянь з n невідомими, яку розв’язуємо методом Жордана-Гаусса.
- Якщо система має 1 розв’язок, то 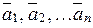утворюють базис і вектор єдиним способом може бути розкладений за цим базисом.
- Якщо система рівнянь має безліч розв’язків або несумісна, то вектори 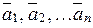базис не утворюють.
Зауваження: Довільний n-вимірний векторний простір має базис, який утворює система одиничних n-вимірних векторів:
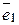= (1; 0; 0;...0) 
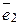= (0; 1; 0;...0)
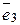= (0; 0; 1;...0) ... 
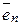= (0; 0; 0;...1)
В тривимірному просторі такими були вектори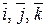 
.
Приклад: чи утворюють вектори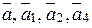 
базис і якщо утворюють , то розкласти за цим базисом:
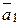= (1; 0; 1; 0) 
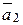= (2; 1; -1; 2) 
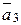= (-1; 1; 2; -1)
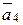= (0; 1; 1; 1) = (2; 2; 2; 1)
Розкласти вектор за даним базисом –значить записати його як лінійну комбінацію базисних векторів.
?
~ 
~
~ 
~ 
~
~ 
~ 
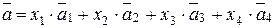
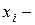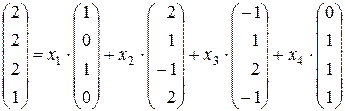
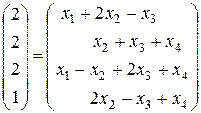
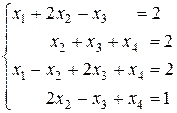
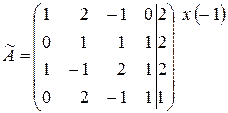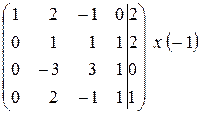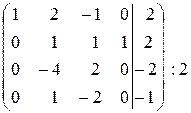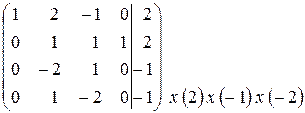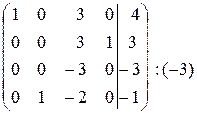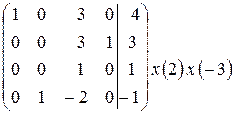
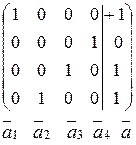
Всі стовпці основної матриці базисні, значить система має 1 розв’язок, а значить вектор можна єдиним способом розкласти за даним базисом. Всі чотири вектори утворюють базис.
х1=1, х2=1 х3=1 х4=0
В новому базисі вектор має координати: =(1; 1; 1; 0).
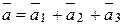
Завдання додому.
1. Конспект; підготовка до практичного заняття.
2. [2] с. 70-76
Питання для самоконтролю
1. n-вимірні векторні простори.
2. Лінійна комбінація векторів.
3. Лінійно залежні та лінійно незалежні комбінації векторів.
4. Базисний мінор.
5. Базис.
6. Розклад вектора за даним базисом.
7. Ранг системи векторів
Л Е К Ц І Я 10
Тема: Пряма лінія на площині
Мета: ознайомити з різними видами рівнянь прямої на площині, кутом між двома прямими, відстанню від точки до прямої
Література: [1, с. 75-83]; [6, с. 131-142].
П Л А Н
1. Різні види рівнянь прямої на площині.
2. Кут між двома прямими.
3. Відстань від точки до прямої.
1. Точка на площині характеризується двома координатами: абсцисою та ординатою (М (х; у)). Рівняння прямої містять координати х та у у першому степені.
1) у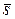 
Нехай дана пряма на площині.
М1 М1 (х1; у1) – фіксована точка прямої.
М (х; у) – довільна точка прямої (змінна)
М
0 х
Вектор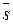 
= (m; n) паралельний прямій.
Потрібно за цими даними скласти рівняння прямої.
Вектори 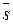і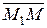 
колінеарні, значить їх координати пропорційні.
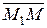= (х-х1; у-у1)
Умова колінеарності:
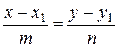
| Канонічне рівняння прямої на площині |
2) Перетворимо одержане рівняння прямої:
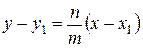
Відношення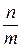 
називають кутовим коефіцієнтом прямої 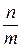=k
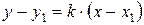
| Рівняння прямої, яка проходить через т. М в |
| напрямі (напрям вказує k) |
у
М1
0 х
 |
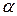- кут нахилу прямої до осі абсцис
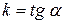
k>0 – кут гострий, k<0 – тупий
3) Перетворимо одержане рівняння:
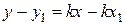
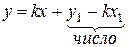
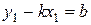
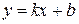
| Рівняння прямої з кутовим коефіцієнтом |
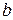– ордината точки, в якій пряма перетинає вісь Оу
 |
у
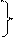
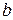
0 х
4) Рівняння прямої, яка проходить через дві задані точки.
у
М2 М1 (х1; у1)
М1 М2 (х2; у2)
 |
0 х Запишемо рівняння прямої:
у-у1=к (х-х1)
у2-у1=к (х2-х1)
Так як М2 (х2; у2) лежить на прямій, то її координати задовольняють рівнянню прямої, тому замість х і у можна підставити координати т. М2 .
Розділимо обидві частини рівнянь і одержимо:
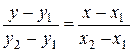
| Рівняння прямої, яка проходить через дві задані точки |
5) Загальне рівняння прямої
 |
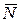М1
М
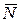=(А; В) 
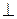прямій
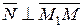
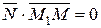
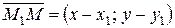
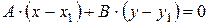
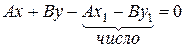
позначимо С
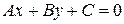
| Загальне рівняння прямої, де А і В – координати |
| нормального вектора прямої, С – вільний член |