Приклад: Чи колінеарні вектори
(-2; 1; -3) і 
(4; -2; -3) ?
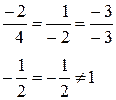
Вектори не колінеарні
Три вектори називаються компланарними, якщо вони лежать в одній площині, або в паралельних площинах.
3. Скалярним добутком двох векторів називається добуток довжин цих векторів на косинус кута між ними
^
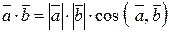-число!
Властивості:
1) 
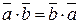
2) 
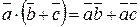
3) 
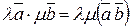
| 4) |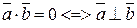 
|
^
5) 
( 
) 
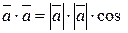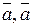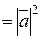, звідки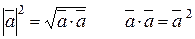 
|
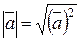
Скалярний добуток двох векторів, заданих координатами в прямокутній системі координат, дорівнює сумі добутків їхніх відповідних координат:
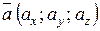
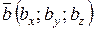
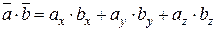
4. Довжина вектора в координатній формі:
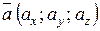
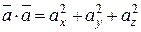
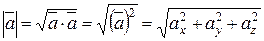
Кут між векторами:
^
^
|
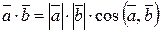
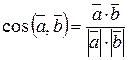
Напрямні косинуси вектора:
у
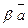
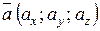
Напрямними косинусами вектора
називаються косинуси кутів, які
0 х вектор утворює з осями координат
Ох, Оу, Оz відповідно.
Тоді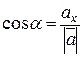 
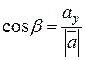
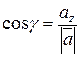
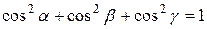(сума квадратів напрямних косинусів довільного вектора дорівнює 1).
Приклади:
1) При якому значенні у вектори будуть перпендикулярними?
(5; -4; 8)
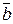(2; у-1; 4)
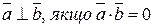
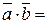10-4 х (у-1)+32=46-4у
46-4у=0, у=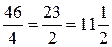 
2) вектори і 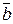колінеарні, знайти х і z:
(х; 3; -2)
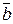(2; 6; -z)
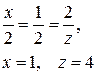
Завдання додому
1. Конспект, підготовка до практичного заняття
2. [1] c. 32-42, 54-58
Питання для самоконтролю
1. Лінійні дії з векторами.
2. Скалярний добуток та його властивості.
3. Довжина вектора, кут між векторами, проекції.
4. Розклад вектора за базисом.
Л Е К Ц І Я 9
Тема: Векторні простори
Мета: сформувати поняття n-вимірного векторного простору; ознайомити з лінійною комбінацією векторів; лінійно залежними та незалежними стемами векторів, базисним мінором, базисом, розкладом вектора за базисом, рангом системи векторів.
Література: [1, с. 50-55]; [6, с. 109-116].
П Л А Н
1. n-вимірні векторні простори. Лінійна комбінація векторів.
2. Лінійно залежні та лінійно незалежні комбінації векторів. Базисний мінор.
3. Базис. Розклад вектора за даним базисом.
4. Ранг системи векторів
n - вимірним вектором називається упорядкована множина n дійсних чисел, які називаються координатами вектора.
n - вимірний вектор можна записати як матрицю-рядок або матрицю-стовпець:
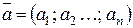або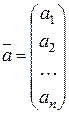 
Число координат вектора називається розмірністю вектора.
Дії з n - вимірними векторами
1) Порівнюють вектори тільки однієї розмірності.
2) 
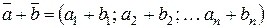
3) 
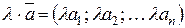
4) 
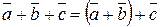або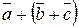 
5) Існує нульовий вектор (всі координати якого дорівнюють 0):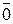 
=(0; 0; ... 0)
6) Існують одиничні вектори (у яких одна з координат дорівнює 1, а інші 0; довжина одиничного вектора дорівнює 1):
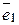=(1; 0; ...0), 
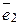=(0; 1; 0;...0), ... 
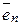=(0; 0; ...1)
7) 
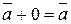
n - вимірним векторним простором називається множина всіх n-вимірних векторів, в якій операції додавання векторів та множення вектора на число визначені, як в пунктах 2 і 3.
Позначається Rn
Зауваження: Простори R1, R2, R3 є окремими випадками простору Rn. Їх можна зобразити геометрично; для n>3 простори Rn геометрично вже уявити не можна, проте вони відіграють важливу роль в науці і техніці.
1) У системі лінійних рівнянь з n невідомими кожне рівняння можна розглядати як (n+1) – вимірний вектор; наприклад перше рівняння: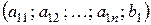 
.
2) Розв’язок системи рівнянь з n невідомими є n-вимірним вектором.
3) Кожний рядок матриці Аmn є n-вимірним вектором, а кожний стовпець m-вимірним. Рядки називаються горизонтальними, а стовпці – вертикальними векторами матриці.