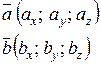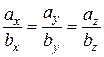Теорема Кронекера –Капеллі*
(критерій сумісності системи)
*Кронекер –німецький математик, Капеллі –італійський
Система лінійних рівнянь сумісна тоді і тільки тоді, коли ранг основної матриці системи дорівнює рангу розширеної матриці: rang А=rang 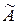 .
.
1) Для сумісної системи:
а) Якщо rang  =rang
=rang 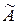 = n, де n –число невідомих системи, то система має
= n, де n –число невідомих системи, то система має
один розв’язок.
б) Якщо rang 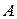 =rang
=rang 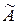 < n, то система має нескінченну множину розв’язків.
< n, то система має нескінченну множину розв’язків.
2) Якщо rang 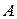 < rang
< rang 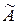 , то система несумісна.
, то система несумісна.
Завдання додому
1. Конспект, підготовка до практичного заняття
2.  с. 29-35
с. 29-35
Питання для самоконтролю
1. Ранг матриці.
2. Методи обчислення рангу.
3. Теорема Кронекера - Капеллі.
Л Е К Ц І Я 7
Тема: Метод Жордана –Гаусса
Мета: ознайомити з методом Гаусса розв’язування систем лінійних рівнянь (інформативно), з методом Жордана-Гаусса, загальним та частинним розв’язками систем лінійних рівнянь
Література: [1, с. 25-31]; [6, с. 80-99].
П Л А Н
1. Метод Гаусса* розв’язування систем лінійних рівнянь (інформативно)
2. Метод Жордана –Гаусса.
3. Загальний та частинний розв’язки систем лінійних рівнянь
* Карл Фрідріх Гаусс (1777-1855) –видатний німецький математик, астроном, фізик, геодезист.
1. Нехай дана система лінійних рівнянь:
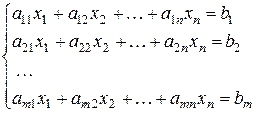
Суть метода Гаусса полягає в тому, що шляхом елементарних перетворень систему треба привести до трикутного вигляду (або трапецевидного (східчастого) вигляду): перше рівняння системи буде містити всі невідомі, крім першого; третє –всі невідомі, крім першого і другого і т.д.:
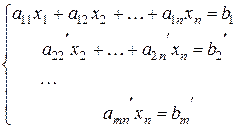
Якщо система рівнянь буде мати один розв’язок, то останнє рівняння буде містити тільки одне останнє невідоме; якщо безліч розв’язків, то крім останнього невідомого останнє рівняння буде містити ще хоча б одне невідоме.
Зворотній хід методу Гаусса: із останнього рівняння знайдемо хn (у випадку 1 розв’язку) або одне із невідомих через послідуючі (у випадку безлічі розв’язків); підставляючи знайдене значення в передостаннє рівняння, знайдемо хn-1 і т.д.
Елементарні перетворення системи
1) Множення (ділення) довільного рівняння системи на число, відмінне від 0.
2) Додавання до обох частин одного з рівнянь системи відповідних частин другого рівняння, помножених на одне й те ж саме відмінне від 0 число.
В результаті елементарних перетворень одержимо еквівалентну даній систему. Еквівалентними (рівносильними) називаються системи, якщо вони мають одні й ті ж розв’язки.
Якщо для даної системи лінійних рівнянь записати розширену матрицю, то після виконання елементарних перетворень по методу Гаусса одержують рівними нулю елементи, що лежать нижче головної діагоналі.
2. Застосовуючи еквівалентні перетворення до системи лінійних рівнянь, можна одержати кожне із рівнянь в такому вигляді, коли кожне із рівнянь містить тільки одне (всі вони різні). Якщо розглядати розширену матрицю системи, то в цьому випадку рівними нулю будуть не тільки елементи, що лежать нижче головної діагоналі, а й ті елементи , що лежать вище головної діагоналі. В цьому заключається метод Жордана*-Гаусса.
* Каміль Жордан (1838-1922) –французький математик
В процесі елементарних перетворень системи можуть бути такі випадки:
1) Одержимо рівняння: 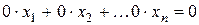
Таке рівняння викидається із системи і система буде містити менше число рівнянь.
2) Одержимо рівняння 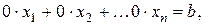 де
де 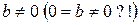 . В цьому випадку система несумісна (розв’язків немає).
. В цьому випадку система несумісна (розв’язків немає).
Зауваження: Так як елементарні перетворення виконуються над рівняннями системи, то в розширеній матриці їх потрібно застосовувати тільки до рядків.
Мета перетворень: в кожному рядку вибрати ведучий елемент; а в кожному стовпці одержати нулі, крім ведучого елемента.
Невідомі, які відповідають базисним стовпцям матриці називаються базисними, а інші невідомі називаються вільними (у випадку, коли система має безліч розв’язків).
3. Загальним розв’язком системи лінійних рівнянь (у випадку безлічі розв’язків) називається розв’язок, в якому базисні невідомі виражені через вільні невідомі.
Частинними розв’язками системи називаються розв’язки, в яких вільні невідомі дорівнюють яким-небудь числам.
До частинних розв’язків належать:
-базисний (якщо усі вільні невідомі дорівнюють 0);
-фундаментальний (якщо одну вільну невідому прирівняти до 1, а інші до 0) (кількість фундаментальних розв’язків залежить від кількості вільних невідомих);
-невід’ємний базисний розв’язок –опорний
Якщо в результаті перетворень матриці одержимо число базисних стовпців рівне числу невідомих, то система має єдиний розв’язок.
Якщо число базисних стовпців менше числа невідомих, то система має безліч розв’язків.
Приклад 1: Розв’язати систему методом Жордана-Гаусса:
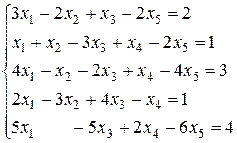

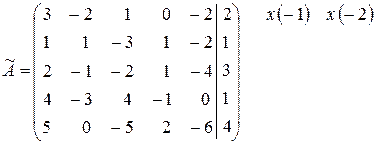 ~
~ 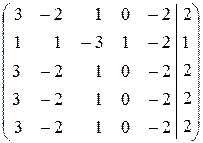 ~
~
~ одержали 4 рядки одинакові –це значить, що в системі буде 4 однакових рівняння, тому 3 з них можна відкинути, тобто в матриці можна викреслити 3 рядки.
~ 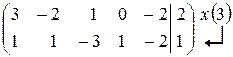 ~
~ 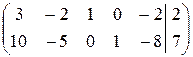
Базисних стовпців 2 (третій і четвертий), а невідомих 5. Так як число базисних стовпців менше числа невідомих, то система буде мати нескінченну множину розв’язків.
х3, х4 –базисні невідомі
х1, х2, х5 -вільні невідомі
Знайдемо загальний розв’язок системи:
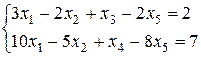
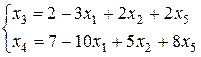 , де
, де 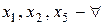
х загал. = 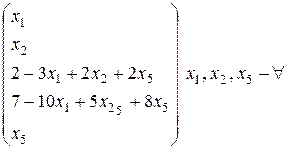
Знайдемо частинний розв’язок:
нехай х1 =1, х2 =3, х5 =-1, тоді
х част. = 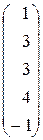
Знайдемо базисний розв’язок х1=х2==х5=0
Х баз. = 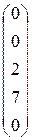
Приклад 2: 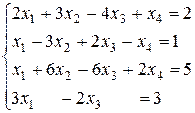

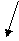
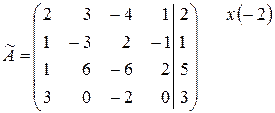 ~
~ 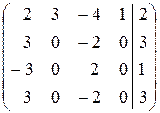 ~
~
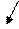 ~
~ 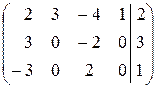 ~
~ 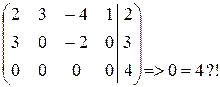
не має змісту
Відповідь: розв’язків немає
Приклад 3: 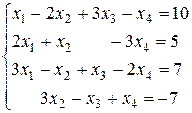

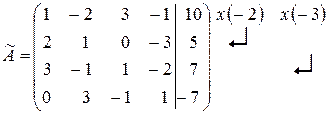 ~
~ 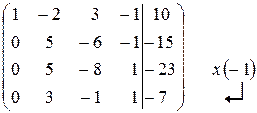 ~
~
 ~
~ 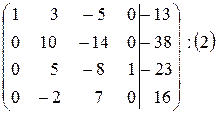 ~
~ 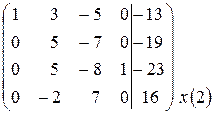 ~
~


 ~
~ 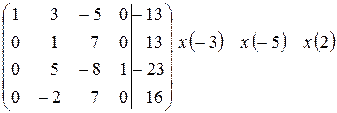 ~
~ 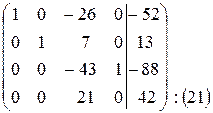 ~
~


 ~
~ 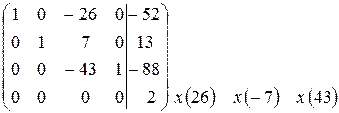 ~
~ 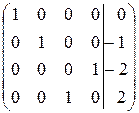
Всі стовпці основної матриці базисні, значить всі невідомі базисні, система має 1 розв’язок:
Завдання додому
1. Конспект, підготовка до практичного заняття
2.  , с. 44-51
, с. 44-51
Питання для самоконтролю
1. Метод Гаусса* розв’язування систем лінійних рівнянь (інформативно)
2. Метод Жордана –Гаусса.
3. Загальний розв’язок систем лінійних рівнянь.
4. Частинний розв’язок систем лінійних рівнянь.
Л Е К Ц І Я 8
Тема: Поняття вектора. Дії з векторами
Мета: сформувати поняття вектора, ознайомити з лінійними діями з векторами, з скалярним добутком та його властивостями, довжиною вектора, кутом між векторами, проекцією, розкладом вектора за базисом.
Література: [1, с. 32-39]; [6, с. 102-107].
П Л А Н
1. Лінійні дії з векторами.
2. Скалярний добуток та його властивості.
3. Довжина вектора, кут між векторами, проекції.
4. Розклад вектора за базисом.
Скалярні величини характеризуються своїм числовим значенням (об’єм, маса, температура…). Векторні* –крім числового значення мають ще й напрям (сила, швидкість…).
*лат. Vector (переносник) ввів у 1848 р. Гамільтон
Геометрично векторна величина зображається напрямленим відрізком:
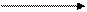
 А
А 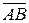 В
В
 Модуль вектора (його довжина) позначається
Модуль вектора (його довжина) позначається 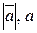 .
.

 До лінійних дій з векторами належать додавання і віднімання векторів, множення вектора на число.
До лінійних дій з векторами належать додавання і віднімання векторів, множення вектора на число.
1) Додавання. 
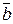
 а) правило трикутника
а) правило трикутника
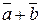
 |
б) правило паралелограма 
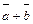

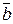

 2) Віднімання
2) Віднімання

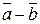

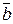
3) Множення вектора на число (скаляр)


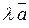
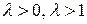
Нульовим називається вектор, початок якого збігається з кінцем ( 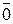 ). Напрям його невизначений, а довжина дорівнює 0.
). Напрям його невизначений, а довжина дорівнює 0.
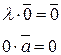
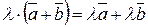
Одиничним називається вектор, довжина якого дорівнює одиниці.
Одиничний вектор, напрям якого збігається з напрямом вектора  називається ортом вектора
називається ортом вектора  і позначається
і позначається 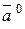
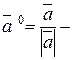 орт
орт
2. 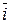 та
та 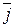 -одиничні вектори на осях х та у в координатній площині.
-одиничні вектори на осях х та у в координатній площині.

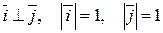
у

 В
В
 у
у 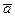



 С
С


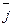
0 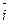 х
х
 х
х
 х – проекція
х – проекція  на Ох
на Ох
 у – проекція
у – проекція  на Оу
на Оу
З 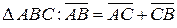

Напрям 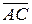 такий же, як і у орта
такий же, як і у орта 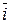 ,
, 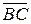 - у орта
- у орта 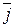 ; довжини:
; довжини:

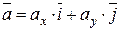
| - розклад вектора за ортонормованим Базисом на площині |
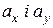 -координати вектора
-координати вектора
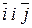 - ортонормований базис на площині.
- ортонормований базис на площині.
Записують так: 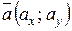
В просторі ортонормований базис утворюють вектори 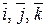
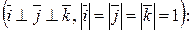
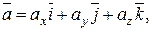

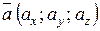
z

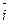
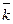



 0
0 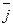 y
y
x
Якщо задано вектор 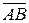 , де А (x1; y1; z1) –початок вектора , В (x2; y2; z2) – кінець, то
, де А (x1; y1; z1) –початок вектора , В (x2; y2; z2) – кінець, то 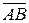 (х2-х1; у2-у1; z2-z1).
(х2-х1; у2-у1; z2-z1).
Дії з векторами в координатній формі.
1) 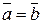 , якщо
, якщо 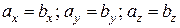
2) 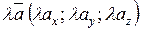
3) 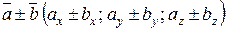
Колінеарними називають вектори, якщо вони лежать на одній прямій або на паралельних прямих.




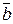
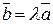 - умова колінеарності векторів, тобто якщо вектори колінеарні, то один з них можна виразити через другий.
- умова колінеарності векторів, тобто якщо вектори колінеарні, то один з них можна виразити через другий.
Якщо вектори задані в координатній формі, то відповідні координати їх пропорційні: