2. Розв’язування матричних рівнянь

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

3. Розв’язування систем лінійних рівнянь за допомогою оберненої матриці.

1. Аналогічно поняттю оберненого числа в теорії чисел вводиться в лінійній алгебрі поняття оберненої матриці, але тільки для квадратних матриць.

Нехай дана квадратна матриця:

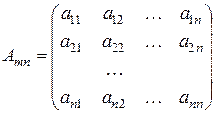
Матриця А^-1 називається оберненою до матриці А якщо при множенні цієї матриці на дану як справа так і зліва одержуємо одиничну матрицю Е:

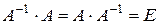
Обернена матриця існує тільки для невиродженої матриці.

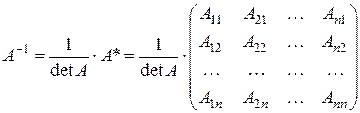
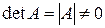
Приклад: Знайти обернену матрицю для матриці А:

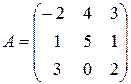
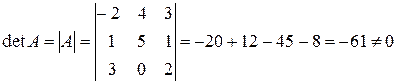
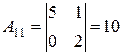
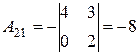
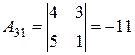
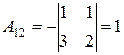
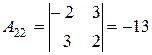
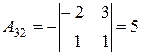
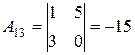
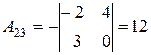
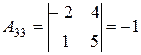
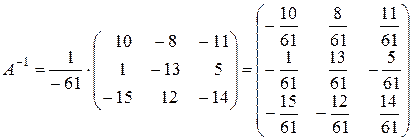
Перевірка: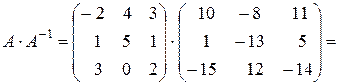

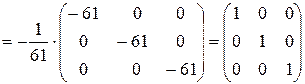
2. АХ=В, де А і В-задані матриці,

Х –невідома матриця

Помножимо обидві частини рівняння зліва на матрицю А^-1.

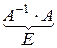
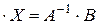, тобто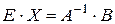

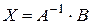
так як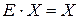

Приклад: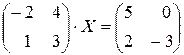

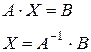
А В

Знайдемо А^-1:

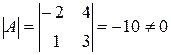
А₁₁= 3 А₂₁= -4

А₁₂= -1 А₂₂= -2

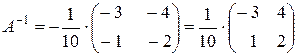
Тоді: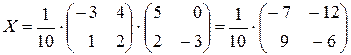

Перевірка: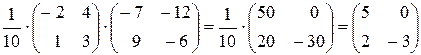

Відповідь: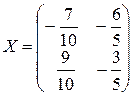

б)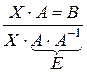

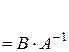
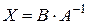
в)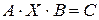

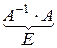
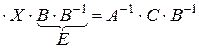
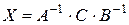
3. Нехай дана система лінійних неоднорідних рівнянь:

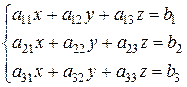
введемо позначення:

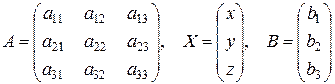
основна матриця системи

Дану систему можна записати за допомогою введених позначень:

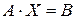
Звідси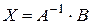

Метод розв’язування систем лінійних рівнянь за допомогою оберненої матриці можна використовувати тоді, коли матриця А невироджена.

Приклад: Розв’язати систему за допомогою оберненої матриці:

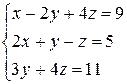
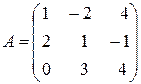
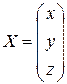
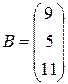
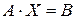, звідси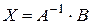

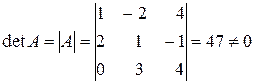
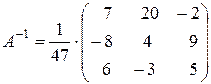
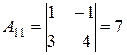
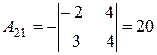
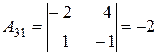
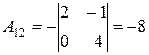
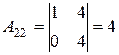
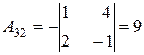
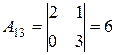
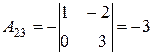
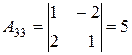
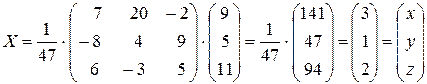
х=3, у=1, z=2

Перевірка: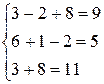

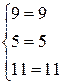
Відповідь: х=3, у=1, z=2

Приклад: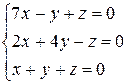

система лінійних однорідних рівнянь

, ,

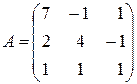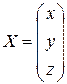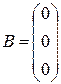
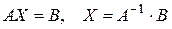
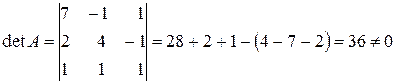
Так як 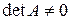, то система має 1 розв’язок (х=0, у=0, z=0).

Якби 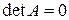, то система мала б нескінченну множину розв’язків.

Завдання додому

1. Конспект, підготовка до практичного заняття.

2.

Питання для самоконтролю

1. Обернена матриця.

2. Розв’язування матричних рівнянь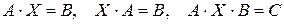

3. Розв’язування систем лінійних рівнянь за допомогою оберненої матриці.

Л Е К Ц І Я 6

Тема: Ранг матриці. Теорема Кронекера-Капеллі

Мета: сформувати поняття ранга матриці; ознайомити з елементарними перетвореннями матриці, теоремою Кронекера-Капеллі

Література: [1, с. 18-20]; [6, с. 68-72].

П Л А Н

1. Ранг матриці.

2. Методи обчислення рангу.

3. Теорема Кронекера-Капеллі.

1. Мінором матриці 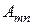k-го порядку називається визначник k-го порядку, який складається з елементів, що знаходяться на перетині будь-яких k рядків та k стовпців.

Обираючи різними способами k рядків та k стовпців, одержимо деяку кількість мінорів k-го порядку.

Матриця має мінори будь-якого порядку: від першого (елементи матриці –мінори 1-го порядку) до найменшого із чисел m та n .

Приклад: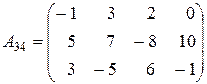

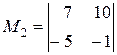
Рангом матриці А (rang А або r (А)) називається найбільший порядок її мінорів, відмінних від нуля.

Властивості:

1) Ранг існує для будь-якої матриці 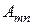, причому .

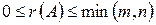2) r (А) =0 тоді і тільки тоді, коли А=0.

3) Для квадратної матриці n-го порядку ранг дорівнює n тоді і тільки тоді, коли матриця невироджена (тобто її визначник не дорівнює 0).

Якщо rang А=r, то любий мінор r-го порядку не рівний 0 називається базисним мінором. Базисних мінорів для матриці може бути декілька.

Якщо rang А=r, то любий мінор k-го порядку дорівнює 0, якщо k > r

2. Ранг матриці простіше всього знайти за допомогою елементарних (еквівалентних) перетворень:

1) перестановка місцями рядків (стовпців) матриці;

2) множення (ділення) всіх елементів любого рядка (стовпця) на будь яке число ;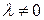

3) додавання до елементів будь-якого рядка (стовпця) відповідних елементів іншого рядка (стовпця), помножених на одне й те саме число;

4) викреслювання (відкидання) нульового рядка (стовпця) (не обов’язково).

Застосовуючи ці перетворення, в результаті одержують еквівалентні матриці, ранги яких однакові:

А~В => rang А = rang В

-За їх допомогою матрицю зводять до матриці, у якої нижче головної діагоналі всі елементи нулі. Тоді ранг матриці дорівнює кількості елементів головної діагоналі, відмінних від 0.

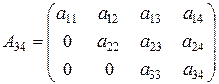rang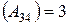

(матриця має вигляд “східців”, її ще називають “трикутною” або “трапецевидною”)

-Другий метод знаходження ранга матриці: за допомогою елементарних перетворень в кожному рядку і в кожному стовпчику матриці одержати не більше одного, не рівного нулю, елемента. В такій матриці ненульові рядки і стовпці називаються базисними рядками і стовпцями. Тоді ранг такої матриці дорівнює числу базисних рядків (стовпців).

Приклад: Знайти rang А:

~ ~

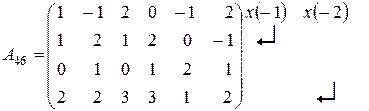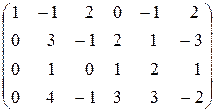х (-2)

~ ~ ~

~

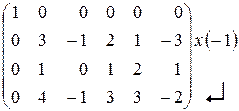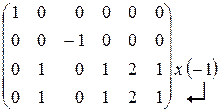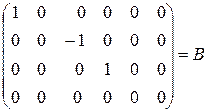
нульові рядки і стовпці викреслюються

Ненульових стовпців (рядків) 3, значить rang В=3, тому і rang А=3.

Мінор, складений з невикреслених елементів (тобто мінор, який складається з елементів базисних рядків і стовпців) називається базисним мінором.

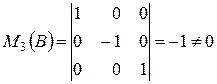
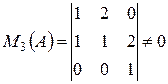
3. Розглянемо систему m лінійних рівнянь з n невідомими:

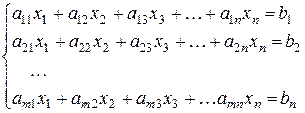
Основна матриця системи –це матриця, елементами якої є коефіцієнти при невідомих:

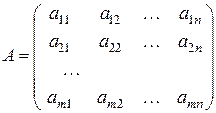
Розширена матриця системи –це матриця основна, до якої дописано матрицю-стовпець вільних членів:

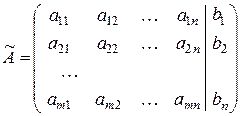
Розв’язком системи називається множина дійсних чисел 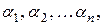підстановка яких у систему замість невідомих 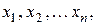перетворює кожне рівняння системи у тотожність.

Система називається сумісною, якщо вона має хоча б один розв’язок. Сумісна система називається визначеною, якщо вона має єдиний розв’язок, і невизначеною, якщо вона має більше одного розв’язку (значить вона має нескінченну множину розв’язків).

Система, що не має розв’язку, називається несумісною.