Мета: сформувати поняття визначника; ознайомити з визначниками 2-го та 3-го порядків, властивостями визначників, теоремою Лапласа, визначниками n-го порядку та їх обчисленням
Міністерство освіти і науки УКРАЇНИ
Харківський інститут фінансів
Українського державного університету фінансів
та міжнародної торгівлі
Кафедра економіко-математичних методів та інформаційних технологій
«ВИЩА МАТЕМАТИКА»
Опорний конспект лекцій
для студентів денної та заочної форми навчання
галузі знань 0305 «Економіка та підприємництво»
напрямів підготовки 6.030508 «Фінанси і кредит»,
6.030503 «Міжнародна економіка»,
6.030509 «Облік і аудит»,
6.030505 «Управління персоналом та економіка праці»
освітньо-кваліфікаційного рівня бакалавр
Укладачі: проф., д.ф.-м.н. Лапшин В.І., ст.викладач Попова О.М.
Розглянуто та ухвалено
на засіданні кафедри
Протокол від 22.09.14 р. № 3
Харків
2014
ЗМІСТ
Лекція 1 Вступна частина. Визначники ____________________________ 4
Лекція 2 Матриці та дії з ними ___________________________________ 9
Лекція 3 Власні числа і власні вектори матриці. Квадратичні форми __ 13
Лекція 4 Розв¢язування систем лінійних рівнянь ___________________ 18
Лекція 5 Розв¢язування систем лінійних рівнянь за допомогою матриць 24
Лекція 6 Ранг матриці. Теорема Кронекера–Капеллі _______________ 29
Лекція 7 Метод Жордана–Гаусса ________________________________ 33
Лекція 8 Поняття вектора. Дії з векторами ________________________ 38
Лекція 9 Векторні простори ____________________________________ 43
Лекція10 Пряма лінія на площині ________________________________ 48
Лекція 11 Площина та пряма в R3 _______________________________ 55
Лекція 12 Функція однієї змінної. Границя функції _________________ 61
Лекція 13 Особливі границі _____________________________________ 66
Лекція 14 Неперервність функції. Похідна. Диференціал функції 
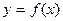____________________________________________________ 71
Лекція 15 Дослідження функцій. Побудова графіків ________________ 76
Лекція 16 Функції багатьох змінних. Частинні похідні ______________ 83
Лекція 17 Похідна за напрямом. Градієнт _________________________ 86
Лекція 18 Екстремум та умовний екстремум функції багатьох змінних _89
Лекція 19 Первісна функція та невизначений інтеграл ______________ 92
Лекція 20 Основні методи інтегрування __________________________ 97
Лекція 21 Інтегрування раціональних дробів _____________________ 100
Лекція 22 Визначений інтеграл _________________________________ 104
Лекція 23 Методи обчислення визначених інтегралів ______________ 108
Лекція 24 Геометричне застосування визначених інтегралів ________ 110
Лекція 25 Невласні інтеграли __________________________________ 114
Лекція 26 Застосування визначеного інтегралу в економіці _________ 117
Лекція 27 Диференціальні рівняння. Основні поняття ______________ 121
Лекція 28 Диференціальні рівняння першого порядку ______________ 123
Лекція 29 Лінійні диференціальні рівняння із сталими коефіцієнтами _125
Лекція 30 Лінійні різницеві рівняння із сталими коефіцієнтами ______ 131
Лекція 31 Числові ряди. Основні поняття ________________________ 134
Лекція 32 Ознаки збіжності рядів _______________________________ 137
Лекція 33 Степеневі ряди _____________________________________ 142
Лекція 34 Ряди Фур’є _________________________________________ 147
Лекція 35 Елементи математичної економіки _____________________ 149
Лекція 36 Математика фінансів ________________________________ 153
Л Е К Ц І Я 1
Тема: Вступна частина. Визначники
Мета: сформувати поняття визначника; ознайомити з визначниками 2-го та 3-го порядків, властивостями визначників, теоремою Лапласа, визначниками n-го порядку та їх обчисленням
Література: [1, с. 6-12]; [6, с. 18-38].
П Л А Н
1. Визначники 2-го та 3-го порядків.
2. Властивості визначників. Розклад визначників за елементами рядка (стовпця.
3. Визначники n-го порядку та їх обчислення.
1. Матриця розміром m x n –це сукупність чисел, розміщених у вигляді прямокутної таблиці, яка має m рядків та n стовпців.
Матриці позначають великими літерами латинського алфавіту та круглими дужками. Така матриця має вигляд:
А=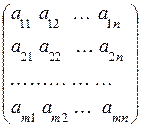 
або А=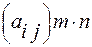 
, A= 
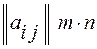
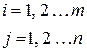
Кожен елемент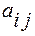 
матриці А має два індекси : перший вказує номер рядка, другий –номер стовпця
Якщо m = n, то матриця буде квадратною.
n –порядок матриці.
Визначник – це число, яке знаходиться з елементів квадратної матриці за певним правилом.
Якщо квадратна матриця позначена літерою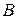 
, то її визначник позначається 
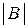або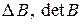 
. Друга назва – детермінант.
Визначники 2-го порядку:
| 
|
|
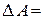
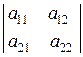
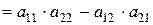
допоміжна головна
діагональ діагональ
(-) (+)
(дорівнює різниці добутків елементів головної та допоміжної діагоналей)
Приклад: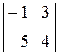 
= 
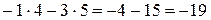
Визначники 3-го порядку:
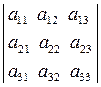
а) Обчислення за правилом трикутників:
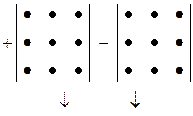
головна допоміжна
діагональ діагональ
(-) (+)
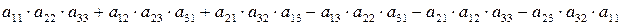
б) Обчислення за правилом Саріуса:
гол. діаг. допом. діаг.
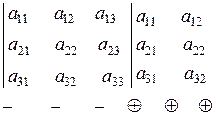
Приклад: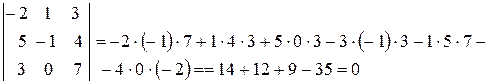 
2. Властивості визначників.
1) Визначник при транспонуванні не змінюється (при заміні рядків на стовпці).
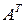- транспонована матриця
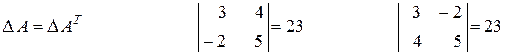
2) Якщо у визначнику поміняти місцями будь-які рядки (або стовпці), то визначник змінить знак на протилежний.
3) Якщо визначник має два однакових рядки (або стовпці), то він дорівнює нулю.
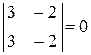
4) Якщо у визначнику усі елементи одного рядка (або стовпця) помножити на дійсне число k, то визначник зміниться також в k разів
Наслідок 1. Спільний множник усіх елементів будь-якого рядка (або стовпця)
визначника можна винести за знак визначника
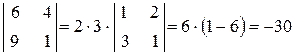
Наслідок 2. Якщо усі елементи будь-якого рядка (або стовпця) визначника
дорівнюють нулю, то визначник дорівнює нулю.
5) Визначник, у якого відповідні елементи двох будь-яких рядків (або стовпців) пропорційні, дорівнює нулю.
Доведення випливає з властивостей 3, 4
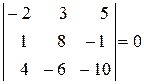
6) Якщо у визначнику елементи будь-якого рядка (або стовпця) є сумою двох доданків, то він дорівнює сумі двох відповідних визначників,
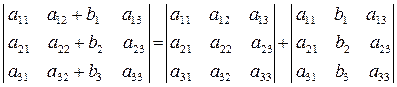
7) Якщо до всіх елементів будь-якого рядка (або стовпця) визначника додати відповідні елементи іншого рядка (або стовпця) цього визначника, помножені на одне й те ж саме число, то визначник не зміниться
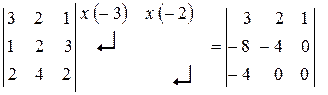
-16 = -16
Для обчислення визначників порядка n > 3 використовують алгебраїчне доповнення.
Мінором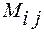 
елемента 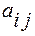з визначника n-го порядку, називається визначник n-1 порядку, який одержуємо з визначника 
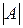шляхом викреслювання і-го рядка та j-го стовпця, на перетині яких знаходиться елемент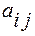
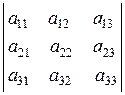
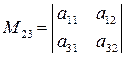
Алгебраїчним доповненням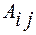 
визначника називається мінор цього елемента, взятий зі знаком 
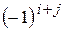, тобто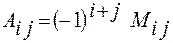 
Приклад: Знайти алгебраїчні доповнення до елементів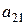 
та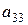 
визначника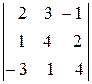 
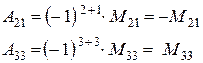
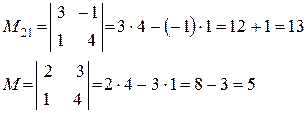
Теорема Лапласа (розкладання визначника за елементами будь-якого рядка або стовпця).
Визначник n-го порядку дорівнює сумі добутків усіх елементів будь-якого рядка (або стовпця) на відповідні їм алгебраїчні доповнення.
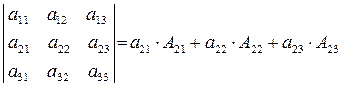
3. Для того, щоб обчислити визначник n-го порядку потрібно до нього застосовувати властивість 7 та теорему Лапласа.
Для скорочення обчислень визначника доцільно його розкласти за елементами такого рядка чи стовпця, який містить найбільшу кількість нулів.
У такому випадку не треба знаходити алгебраїчні доповнення до елементів, що дорівнюють 0 (добуток 0 на будь-яке алгебраїчне доповнення дорівнює 0). Треба навчитись виконувати еквівалентні перетворення визначника, які дають можливість одержати нулі у деякому рядку або стовпці.
Приклад: Обчислити визначник 4 порядку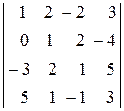 
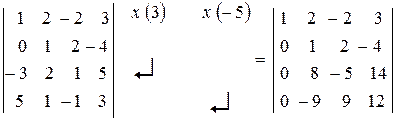
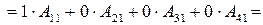
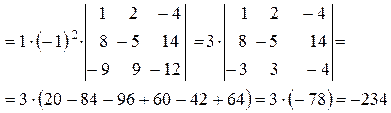
Завдання додому
1. Конспект; підготовка до практичного заняття
2. [2] , с. 16-26
3. [4] , с. 81-88
Питання для самоконтролю
1. Визначники 2-го порядку.
2. Визначники 3-го порядку.
3. Властивості визначників.
4. Розклад визначників за елементами рядка (стовпця).
5. Визначники n-го порядку та їх обчислення.
Л Е К Ц І Я 2
Тема: Матриці та дії з ними
Мета: сформувати поняття матриці; розглянути застосування матриці в економіці, ознайомити з діями з матрицями та їх властивостям
Література: [1, с. 13-18]; [6, с. 44-61].
П Л А Н
1. Поняття матриці. Застосування матриці в економіці.
2. Дії з матрицями, властивості.
1. Матрицею* розміром m x n називають сукупність чисел, розміщених у вигляді прямокутної таблиці, яка має m рядків та n стовпців.
*(поняття матриці вперше ввели англійські математики Гамільтон і Келі)
Матриці позначають великими літерами латинського алфавіту та круглими дужками. Така матриця має вигляд:
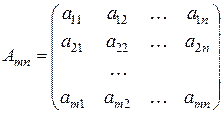
або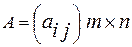 
, 
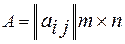
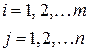
Кожен елемент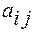 
матриці А має два індекси: перший вказує номер рядка, другий –номер стовпця.
*матриці широко використовуються в плануванні виробництва та транспортних перевезень. Вони дозволяють розробляти різні варіанти плану, полегшують дослідження залежності між різними економічними показниками
За формою матриці можуть бути прямокутними (m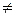 
n), квадратними ( m = n ), матриця-рядок (у якої всього один рядок), матриця-стовпець ( у якої всього один стовпець).
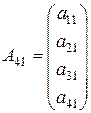
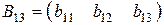
2. Дії з матрицями:
Порівнювати матриці можна одного розміру. Матриці рівні тоді, коли
рівні їх відповідні елементи.
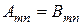
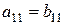
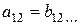
1) Транспонувати матрицю –значить замінити її рядки стовпцями або навпаки.
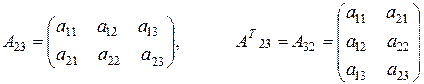
2) Додавати (віднімати) можна матриці одного розміру. Щоб додати дві
матриці , потрібно додати їх відповідні елементи.
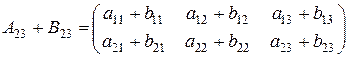
3) Добуток матриці на число:
щоб помножити матрицю на число , потрібно кожний елемент її помножити на це число
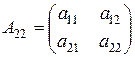
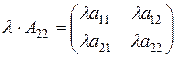
З цього випливає, що за знак матриці можна виносити спільний множник всіх елементів.
Приклад: Виконати дії:
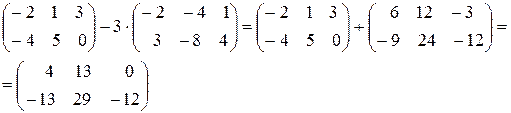
Діагональною матрицею називається квадратна матриця, в якої всі елементи, крім елементів, які знаходяться на головній діагоналі, дорівнюють нулю.
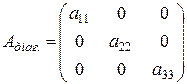
Одиничною матрицею називається діагональна матриця, у якої кожен елемент головної діагоналі дорівнює одиниці
Е=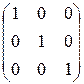 
Нульовою матрицею називається матриця, у якої всі елементи дорівнюють нулю.
4) Добуток матриць
Матриці можна перемножати тоді, коли число стовпців першої матриці дорівнює числу рядків другої матриці
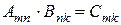
(такі матриці називаються узгодженими)
Правило множення рядка на стовпець:
11 
Схема: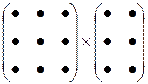 
Щоб визначити елементи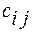 
, потрібно кожний елемент i-го рядка першої матриці помножити на відповідні елементи j-го стовпця другої матриці і результати (добутки) додати.
Приклад: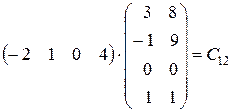 
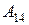
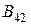
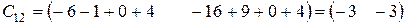
2) 
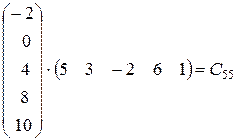
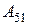
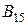
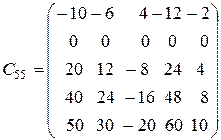
Властивості додавання:
1) А+В=В+А (комутативність)
2) А+(В+С)=(А+В)+С (асоціативність)
3) А+0=А (роль 0 матриці як числа 0)
4) 
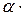
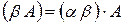
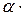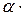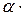5) (А+В)= А+ В
6) 
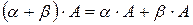
Властивості множення:
1) 
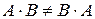(іноді 
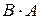не має змісту),
Якщо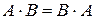 
, то такі матриці називаються переставними
2) 
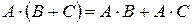розподільний закон множення відносно додавання
3) 
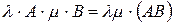
4) 
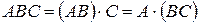
5) 
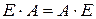(роль Е матриці як числа 1)
Приклад: Знайти добуток:
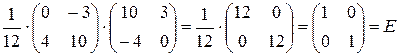
3. Якщо в квадратній матриці всі елементи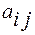 
замінити на відповідні алгебраїчні доповнення 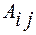, потом транспонувати матрицю, то одержимо матрицю, яка називається приєднаною:
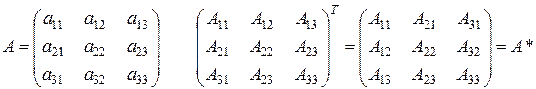
Визначником (детермінантом) квадратної матриці А називається визначник, елементами якого є елементи матриці:
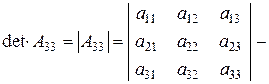число!
Квадратна матриця називаються виродженою (особливою), якщо її визначник дорівнює нулю.
Квадратна матриця називається невиродженою (неособливою), якщо її визначник не дорівнює нулю.
Завдання додому
1. Конспект, підготовка до практичного заняття.
2. [2], с. 26-29
Питання для самоконтролю
1. Поняття матриці.
2. Застосування матриці в економіці.
3. Дії з матрицями, властивості.
Л Е К Ц І Я 3
Тема: Власні числа і власні вектори матриці. Квадратичні форми
Мета: сформувати поняття лінійного оператора; ознайомити з власними числами і власними векторами матриці, квадратичними формами
Література: [1, с. 16-18]; [6, с. 47-57].
П Л А Н
1. Лінійні оператори