Правильные многогранники
Выпуклый многогранник называется правильным, если:
1. все его грани — равные правильные многоугольники;
2. в каждой его вершине сходится одно и то же число рёбер.
Все рёбра правильного многогранника равны, а также равны все двугранные углы, содержащие две грани с общим ребром.
Возникают вопросы:
1. какие правильные многоугольники могут быть гранями правильного многогранника?
2. Сколько граней может иметь правильный многогранник?
Не существует правильного многогранника, гранями которого являются правильные многоугольники, если число их сторон 6 или больше, то есть правильные n-угольники, если n≥6.
1. У правильного n-угольника, если n≥6, углы не меньше 120°.
2. В каждой вершине многогранника должно быть не меньше трёх углов.
3. Даже при трёх углах сумма всех углов уже достигает 360°.
4. Сумма всех плоских углов при каждой вершине выпуклого многогранника меньше 360°.
Следовательно, не существует правильного многогранника, гранями которого являлись бы правильные n-угольники, если n≥6.
Только правильные треугольники, четырёхугольники (квадраты) и пятиугольники могут быть гранями правильного многогранника.
Существуют ли правильные многогранники с такими гранями, и сколько граней они имеют? Очевидно, меньшее возможное число граней — четыре.
Существующие правильные многогранники
тетраэдр с 4 гранями, 6 рёбрами и 4 вершинами:
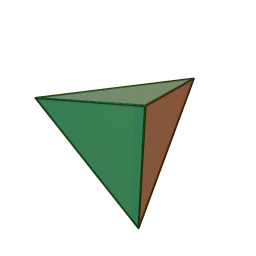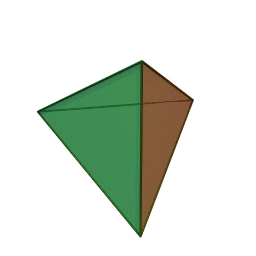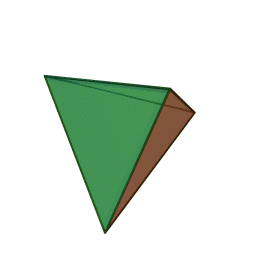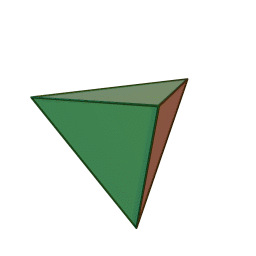
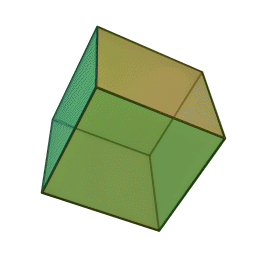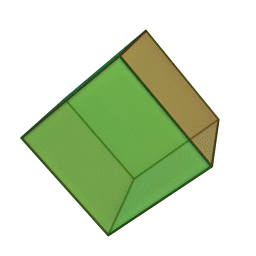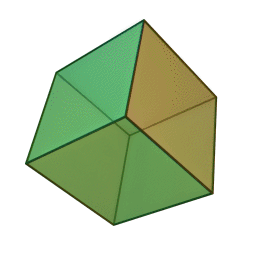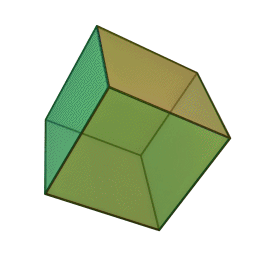
куб с 6 гранями, 12 рёбрами и 8 вершинами:
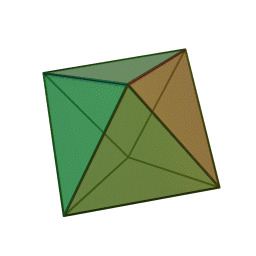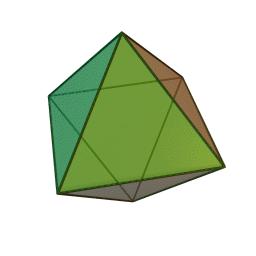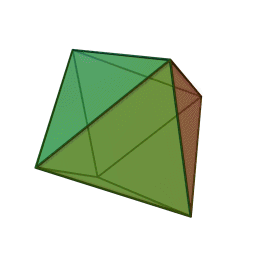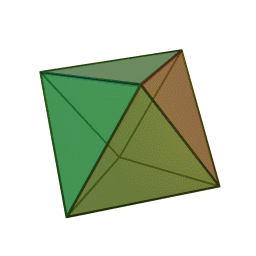
октаэдр с 8 гранями, 12 рёбрами и 6 вершинами:
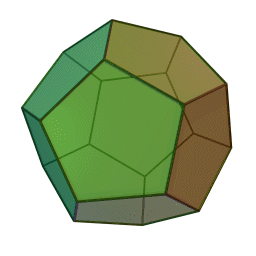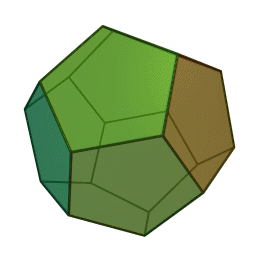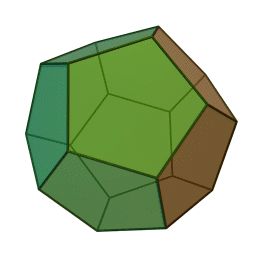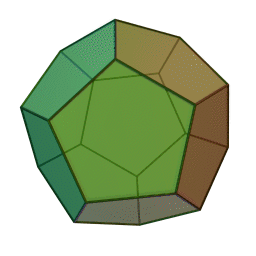
додекаэдр с 12 гранями, 30 рёбрами и 20 вершинами:
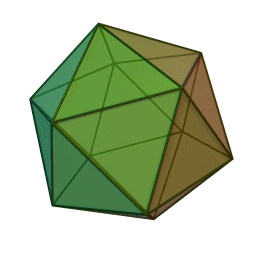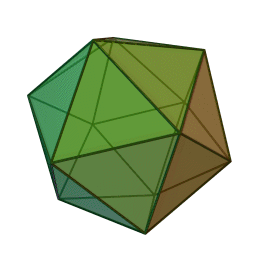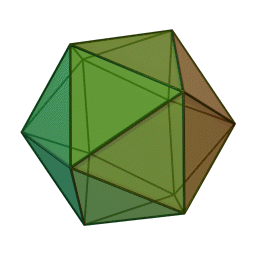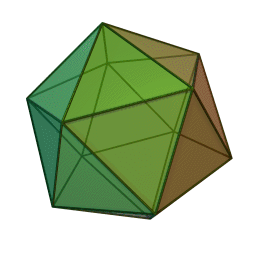
икосаэдр с 20 гранями, 30 рёбрами и 12 вершинами: