Основные факты о правильных многоугольниках
Вспомним основные факты о правильных многоугольниках (см. рис. 1). У таких многоугольников все стороны и углы равны (это просто их определение). Сторону и угол правильного n-угольника обычно обозначают: и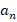 
. Так, например, 
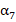и 
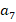– это сторона и угол правильного семиугольника.
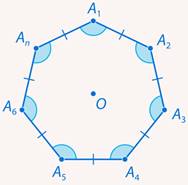
Рис.1. Правильный многоугольник
Правильный n-угольник (если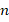 
задано) задается всего одним параметром – длиной своей стороны. Все остальные элементы будут определяться этой величиной.
Если известно количество вершин правильного n-угольника, то есть число 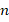, то мы можем найти величину внутреннего угла (так как умеем вычислять сумму углов произвольного многоугольника, а в правильном многоугольнике все углы равны).
Сумма углов произвольного n-угольника равна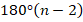 
. Разделив ее на количество углов, получаем формулу угла правильного многоугольника:
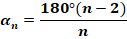
Вокруг любого правильного многоугольника всегда можно описать окружность, и в него всегда можно вписать окружность (см. рис. 2). Радиусы таких окружностей мы обычно обозначаем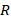 
и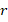 
(при необходимости – с индексом ).
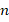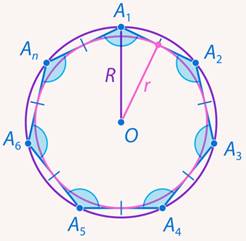
Рис. 2. Вписанная и описанная окружности около правильного многоугольника
Площадь любого описанного многоугольника, в том числе правильного, выражается через радиус вписанной окружности:
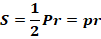
Сторона и радиус описанной окружности правильного многоугольника связаны формулой:
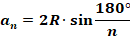
Ее несложно вывести, используя определение синуса для соответствующего прямоугольного треугольника.
Так же можно получить формулу, связывающую сторону и радиус вписанной окружности:
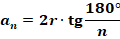
Это и есть основные наши знания о правильных многоугольниках. Потренируемся, используя эту информацию, решать различные задачи.
Нахождение углов и вершин правильного многоугольника
Задача 1. Найти углы правильного 
-угольника (см. рис. 3).
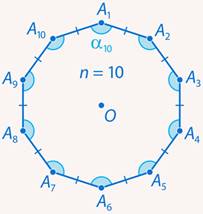
Рис. 3. Иллюстрация к задаче 1
Решение
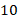Используем известную нам формулу (или просто делим сумму углов -угольника на , чтобы найти один из одинаковых углов):
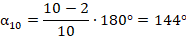
Ответ: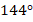 
.
Задача 2. Сколько вершин в правильном многоугольнике, каждый угол которого равен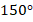 
(см. рис. 4)?
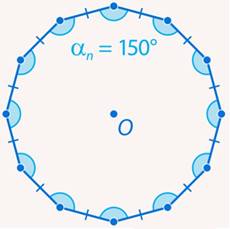
Рис. 4. Иллюстрация к задаче 2
Решение
Это задача, обратная предыдущей. Для решения используем ту же самую формулу:
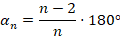
Теперь мы знаем величину угла, подставим ее и решим полученное уравнение относительно :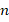
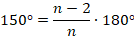
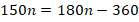
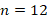
Ответ: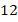 
.
Задача 3. Сколько вершин у правильного многоугольника, сторона которого стягивает дугу описанной окружности, равную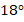 
(см. рис. 5)?
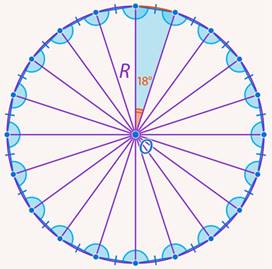
Рис. 5. Иллюстрация к задаче 3
Решение
Вся окружность составляет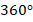 
. Наш многоугольник разбивает ее на дуги по 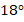. Количество таких дуг:
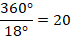
Значит, мы имеем дело с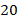 
-угольником.
Ответ: .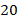
Нахождение площади правильного многоугольника
Задача 4. Найти площадь правильного многоугольника, есл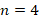и 
и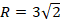 
.
Решение
Можно использовать формулу для вычисления площади произвольного описанного многоугольника:
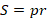
Поскольку параметр, определяющий правильный многоугольник, – это его сторона (через нее мы умеем выражать все остальные необходимые нам элементы), то с нее мы и начнем.
Мы знаем, что:
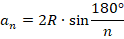
Подставляем в нее известные нам из условия данные, получаем:
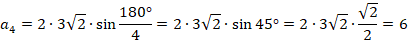
Тогда:
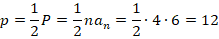
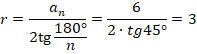
Теперь найти площадь не составит труда:
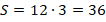
Ответ: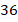 
.
Такой метод позволяет решать задачи «в лоб», не задумываясь о том, какие именно данные нам известны. Если вы помните формулы, то даже рисунок для решения такой задачи не нужен. В этом большой плюс такого универсального метода.
Но в данном случае, если задуматься о конкретном типе многоугольника, задача решается намного быстрее. Как только мы сообразим, что правильный многоугольник, у которого 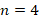, – это квадрат, а радиус описанной окружности – это половина его диагонали (см. рис. 6), то задача упрощается до такой: найти площадь квадрата, если его диагональ равна:
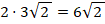
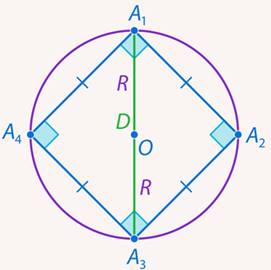
Рис. 6. Квадрат, вписанный в окружность радиуса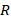
Сторона квадрата в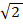 
раз короче его диагонали (если не помните, почему так, проверьте с помощью теоремы Пифагора), то есть:
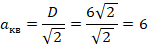
Тогда:
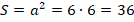
Задача 5. Найти площадь правильного многоугольника, если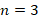 
, а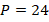 
.
Решение
Итак, понятно, что речь идет о равностороннем треугольнике (см. рис. 7) с периметром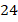 
. Значит, мы знаем его стороны:
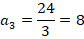
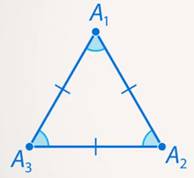
Рис. 7. Иллюстрация к задаче 5
Найти его площадь мы можем, как используя универсальный метод для правильного многоугольника (в котором не используются свойства конкретно треугольника), так и рассматривая частный случай равностороннего треугольника.
Способ 1. Проведем высоту в равностороннем треугольнике (см. рис. 8).
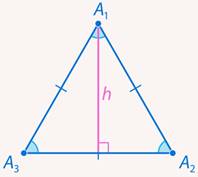
Рис. 8. Иллюстрация к задаче 5
Мы можем ее найти или по теореме Пифагора, или умножив гипотенузу на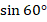 
:
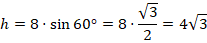
Площадь треугольника равна половине произведения основания на высоту:
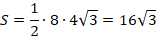
Способ 2. Используя формулу для стороны правильного -угольника, найдем радиус вписанной окружности (см. рис. 9):
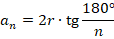
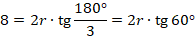
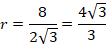
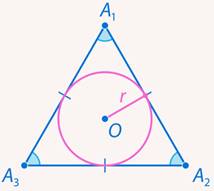
Рис. 9. Иллюстрация к задаче 5
Найдем площадь, используя формулу для вычисления площади произвольного описанного четырехугольника:
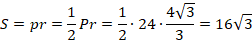
Ответ: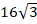 
.
Задача 6. Найти площадь правильного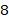 
-угольника, если 
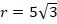(см. рис. 10).
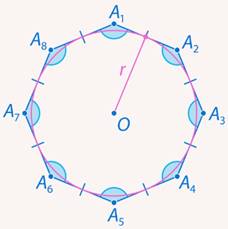
Рис. 10. Иллюстрация к задаче 6
Решение
Снова будем использовать формулу:
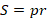
Радиус вписанной окружности нам дан, осталось найти полупериметр. Периметр – это сумма длин всех сторон, в правильном 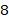-угольнике их 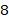и они все равны, поэтому нужно найти длину одной стороны. Используем формулу радиуса вписанной окружности:
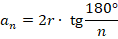
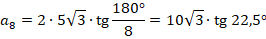
Значения тангенса такого угла в нашей таблице нет, поэтому пока оставим выражение в таком виде. Подставим в формулу для вычисления площади, получим:
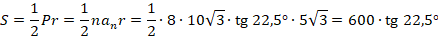
Вычислим значение тангенса на калькуляторе (или найдем его по таблице Брадиса) и получим приближенное значение площади:
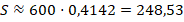
Ответ: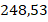 
.
Задача 7. Найти отношение площадей двух шестиугольников – описанного вокруг данной окружности и вписанного в нее (см. рис. 11).
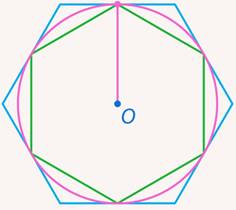
Рис. 11. Иллюстрация к задаче 7
Решение
Первый способ универсальный. Для одного из шестиугольников окружность будет вписанной, а для другого – описанной. Обозначим ее радиус за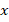 
. Тогда площадь описанного шестиугольника, как мы знаем, вычисляется по формуле:
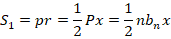
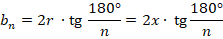
Тогда:
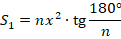
Площадь вписанного шестиугольника выразить через 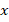немного сложнее. Для него данная окружность уже будет описанной. Получаем:
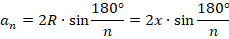
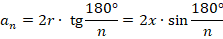
Откуда:
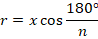
Получаем:
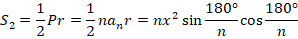
Тогда:
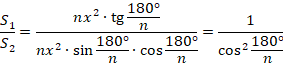
В случае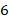 
-угольника получаем:
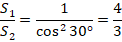
Ответ: 
.
Обратите внимание, что мы нигде (до самого последнего действия) не использовали то, что речь идет о шестиугольниках. То есть можно сказать, что мы решили такую задачу для произвольных n-угольников (в общем виде).
Теперь попробуем решить эту задачу, используя то, что правильные шестиугольники обладают некоторыми особенными свойствами.
Правильный шестиугольник состоит из шести равносторонних треугольников, и стороны этих треугольников равны радиусу описанной окружности (см. рис. 12). Тогда малый шестиугольник состоит из шести треугольников со стороной .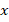
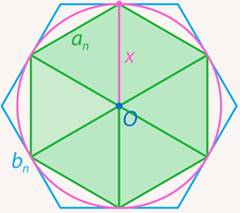
Рис. 12. Малый шестиугольник состоит из шести треугольников со стороной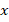
Большой шестиугольник состоит из треугольников, где 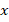является высотой (см. рис. 13). Сторона такого треугольника равна:
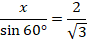
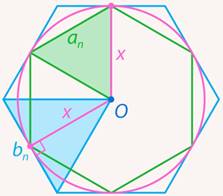
Рис. 13. Большой шестиугольник состоит из треугольников, где 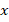является высотой
То есть сторона малого шестиугольника равна 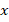, а большого – 
.
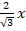Площади подобных фигур относятся как квадраты их соответствующих линейных размеров:
