Формула скалярного произведения двух векторов и
Через их координаты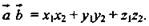 
Скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.
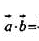
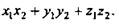
Угол между векторами.
Косинус угла между векторами пространства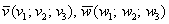 
, заданными в ортонормированном базисе 
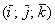, выражается формулой:
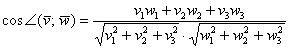
Сформулируем основные свойства скалярного произведения векторов.
Для любых векторов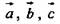 
и любого числа k справедливы равенства:
1) 
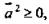причем 
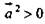при 
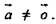
2) 
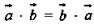(переместительный закон).
3) 
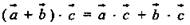(распределительный закон).
4) 
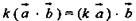(сочетательный закон).
Вычисление углов между прямыми и плоскостями.
Угол между двумя прямыми (пересекающимися или скрещивающимися), если известны координаты направляющих векторов.
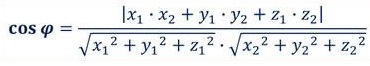
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Дано: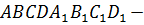 
прямоугольный параллелепипед, где 
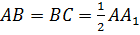. Найт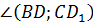и 
и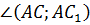 
.
Решение: ранее в таких случаях мы пытались по рисунку находить величины углов.
Но теперь мы владеем формулой косинуса угла между прямыми.
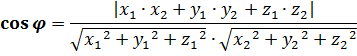
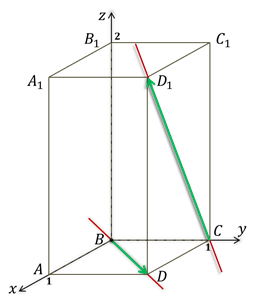Только для этого необходимо знать координаты направляющих векторов прямых. В данном случае, для прямой BD направляющим может является вектор BD , а для прямой
CD- CD вектор (рис. 15)
Для удобства изобразим прямоугольную систему координат так, чтобы точка B совпадала с точкой начала координат. Взяв длину рёбер AB и BC за единичные отрезки, можно утверждать, что длина отрезка BB равна 2.
Тогда не трудно определить координаты точек B, D, C и D1.
Точка B(0;0;0). Точка D(1;1;0). Точка C(0;1;0) . А точка D(1;1;2).
Теперь не трудно найти координаты векторовBD и CD как разности соответствующих координат конца и начала вектора.
Получаем, что вектор BD {1-0;1-0;0-0}. А вектор
CD{1-0;1-1;2-0}.
Теперь можем воспользоваться формулой косинуса угла между прямыми. Подставим координаты направляющих векторов.
Рис. 15
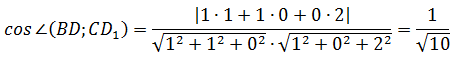
Ответ: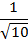 
Пример 2.
Дано: DABC – пирамида; DA ⊥ DB ⊥ DC; DA = DB = DC = а.
Найдите: косинус угла между прямыми DC и CM (СМ – высота треугольника АВС), поставьте ему в соответствие верный вариант ответа из предложенных ниже:
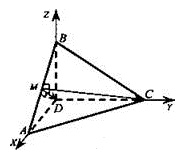
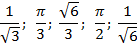
Решение:
Треугольник АВС правильный, поэтому тоска М является серединой стороны АВ.
Введем систему координат как показано на рисунке.
Найдем координаты векторов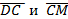 
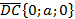
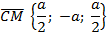
Применив формулу косинуса угла между векторами, получим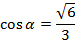 
.
Ответ: 