Прототип (объявление) функции

Дата: 2025-05-25; Просмотры: 4

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

тип_результата имя_функции (спецификация параметров);

Определение функции

тип_результата имя_функции (список формальных параметров)

{

операторы;

}

Вызов функции

имя_функции (список фактических параметров)

Фактические параметры передаются в функцию по значению и должны соответствовать формальным по количеству, типу и смыслу.

Указатель на функцию

тип_результата ( * имя_указателя) (спецификация параметров);

Постановка задачи

Написать три программы согласно индивидуальному варианту задания. Для первой и второй программ функции ввода и вывода массивов описывать отдельно, не объединяя с обработкой данных. Можно сохранить эти функции в отдельном файле и использовать в обеих программах, включив содержимое этого файла в текст программы с помощью директивы # include.

В третьей программе определить функцию Integral() для приближенного вычисления определенного интеграла вида 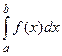указанным методом. Использовать эту функцию для вычисления значений двух интегралов, передавая подынтегральную функцию в функцию Integral() в качестве параметра.

Формулы численного интегрирования

Пусть на отрезке [a , b] задана непрерывная функция y = f(x). Требуется вычислить определенный интеграл 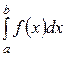. Разделим отрезок [a , b] точками a=x₀, x₁, x₂, …, x_n=b на n равных частей длины Dx: 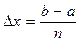. Обозначим далее через y₀, y₁, y₂, …, y_n значения функции f(x) в точках x₀, x₁, x₂, …, x_n, т. е. y₀=f(x₀), y₁=f(x₁), y₂=f(x₂), …, y_n=f(x_n). Значение интеграла определяется по одной из формул:

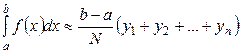– формула прямоугольников

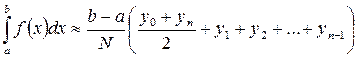– формула трапеций

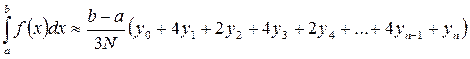– формула парабол

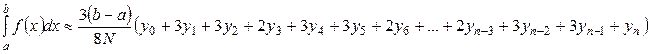– формула Ньютона

Варианты заданий

Вариант 1

1. Поменять местами максимальные элементы массива А (45) и матрицы В (6х9). Если в массиве максимальное значение имеют несколько элементов, массив считается некорректным.

2. Определить, состоят ли целочисленные массивы А (16) и В (18) из одинаковых наборов значений. Элементы в массивах могут располагаться в произвольном порядке, одно и то же значение может встречаться неоднократно.

3. 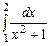, , 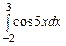, 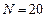метод трапеций

Вариант 2

1. Отсортировать массив М (50) и каждую строку матрицы А (6х7) в порядке убывания.

2. Удалить из матрицы А (7х5) все строки, сумма элементов которых четна, а из матрицы В (6х8) – строки, сумма элементов которых нечетна, передвинув на их место следующие строки без на­рушения порядка их следования.

3. 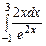, , 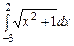, 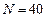метод трапеций

Вариант 3

1. Дана квадратная целочисленная матрица С. Если в ней есть строки, состоящие из нулей, то обнулить столбцы с такими же номерами. Если есть столбцы, состоящие из нулей, то обнулить соответствующие строки. Обнуления выполнять до тех пор, пока в матрице не останется непарных нулевых строк и столбцов. Вывести на экран номера строк и столбцов, в которых остались ненулевые элементы. Действия над одной строкой или одним столбцом оформить функциями.

2. Даны 2 одномерных массива: А из 10 элементов и В из 15 элементов. Сформировать 2 новых массива: массив Х из элементов массива А, не входящих в массив В, и массив У из элементов массива В, не входящих в А.

3. 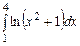, , 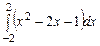, 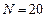метод прямоугольников

Вариант 4

1. В матрицах А (10х15) и В (15х10) заменить все совершенные числа нулями. Совершенным называется натуральное число N, равное сумме всех своих делителей, меньших самого N.

2. Допустимым преобразованием матрицы назовём перестановку двух соседних строк или двух соседних столбцов. Дана вещественная квадратная матрица порядка n (n£12). С помощью допустимых преобразований получить матрицу, в которой максимальный элемент располагается в левом верхнем углу. Использовать функции для выполнения допустимых преобразований и для нахождения индексов максимального элемента.

3. 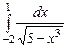, , 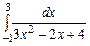, 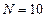метод парабол

Вариант 5

1. Определить, сколько в матрице А (8х6) строк, среднее арифметическое значение элементов которых больше среднего арифметического значения элементов массива В (18).

2. Удалить из матрицы А (5х7) все столбцы, содержащие не менее 2 отрицательных элементов, а из матрицы В (7х7) – столбцы, содержащие не менее 3 отрицательных элементов, передвинув на их место следующие столбцы без на­рушения порядка их следования.

3. 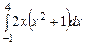, , 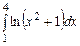, 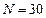метод прямоугольников

Вариант 6

1. Поменять местами минимальные элементы массива А (57) и матрицы В (7х5). Массивы, содержащие более одного минимального значения, признаются некорректными.

2. Удалить из матрицы А (6х9) все строки, содержащие единицы, а из матрицы В (6х7) – строки, содержащие нули, передвинув на их место оставшиеся строки без на­рушения порядка их следования.

3. 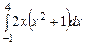, , 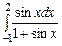, 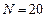метод парабол

Вариант 7

1. Вычислить среднее арифметическое значение элементов, лежащих на диагоналях матриц А (5х5) и С (6х6). Заменить этим значением все элементы обеих матриц, не лежащие на диагоналях.

2. Даны два вектора Y и X размерности n = 30. Вычислить 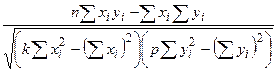, где k – порядковый номер максимального элемента вектора X, а p – порядковый номер максимального элемента вектора Y. Массивы, в которых более одного элемента имеют максимальные значения, считать некорректными.

1. 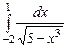, , 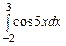, 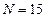метод Ньютона

Вариант 8

1. Найти сумму наибольших из отрицательных элементов матрицы А (7х8) и массива В (76).

2. Подсчитать количество элементов массива Р (60), отличающихся от среднего арифметического значения элементов массива М (70) не более чем вдвое, и количество элементов массива М, отличающихся от среднего арифметического значения массива Р не более, чем втрое.

3. 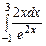, , 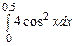, 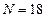метод Ньютона

Вариант 9

1. Заданный массив целых чисел А делится на три части двумя элементами: максимальным и минимальным. Взаимное расположение максимума и минимума может быть любым. Определить среднее арифметическое четных значений в каждой части массива. Использовать функции для нахождения положения минимального и максимального элементов и подсчёта среднего в одной части массива. Массивы, состоящие из одинаковых элементов, а также массивы, в которых более одного элемента имеют максимальное или минимальное значение, признаются некорректными.

2. Поменять местами наименьшие из положительных элементов массивов А (55) и В (8х7). Массивы, не содержащие положительных элементов или содержащие более одного элемента с минимальным положительным значением, признаются некорректными.

3. 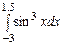, , 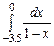, 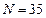метод прямоугольников

Вариант 10

1. Даны матрицы Q (12x9) и С (7x8). Вставить после столбцов с максимальными элементами столбцы из нулей, сдвинув последующие. Количество столбцов в матрицах после вставки должно увеличиться

2. Отсортировать элементы нечетных строк матрицы А (6х7) и четных строк матрицы В (9х6) в порядке убывания, а элементы четных строк матрицы А и нечетных строк матрицы В – в порядке возрастания.

3. 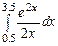, , 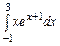, 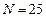метод парабол

Вариант 11

1. В заданном массиве М (50) найти максимум и минимум. Расположить элементы массива таким образом, чтобы к максимуму они возрастали, а к минимуму убывали. Положение максимального и минимального элементов изменять запрещено, их расположение в массиве может быть любым. Корректными считать только массивы, содержащие значения максимума и минимума в единственном экземпляре.

2. Составить программу вычисления произведения двух прямоугольных целочисленных матриц А и В. Вычисление одного элемента результирующей матрицы оформить функцией. При задании матриц контролировать совпадение числа столбцов первой матрицы с числом строк второй.

3. 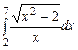, , 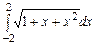, 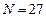метод Ньютона

Вариант 12

1. В матрице A (m,n), состоящей из нулей и единиц, найти квадрат заданного размера (квадратную подматрицу), состоящий целиком из нулей.

2. Дана матрица D размера nхm( n,m £ 20). Сформировать 3 одномерных массива: А – из элементов матрицы D, лежащих в диапазоне от -5 до 5, в порядке следования по строкам, В – из элементов от 10 до 20, С – от 30 до 50. Использовать подпрограмму для выборки в новый массив элементов одного диапазона.

3. 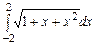, , 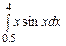, 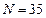метод трапеций

Вариант 13

1. Поменять местами наибольшие по модулю элементы матрицы А (7х8) и массива В (76). Если в массиве наибольшее по модулю значение встречается неоднократно, такой массив признается некорректным.

2. Даны матрицы В (m,n) и С (n,m). Определить, есть ли в заданных матрицах строки, содержащие по два положительных элемента. Вывести номера таких строк.

3. 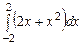, , 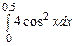, 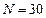метод прямоугольников

Вариант 14

1. Поменять местами первый максимальный элемент массива А (60) и последний максимальный элемент массива В (85).

2. Даны два вектора Y (30) и X (30). Вычислить значение функции 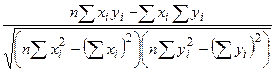. Сумму элементов одного массива и сумму квадратов элементов одного массива оформить отдельными функциями.

1. 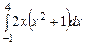, , 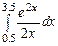, 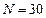метод Ньютона

Вариант 15

1. Подсчитать общее количество простых чисел среди элементов целочисленных массивов X (50) и Y (12х5). Простым называется натуральное число, не имеющее других делителей, кроме 1 и значения самого числа.

2. Даны два целочисленных массива: P (46) и Q (39). Сформировать новый массив из элементов массивов P и Q, присутствующих в них обоих, из исходных массивов эти элементы удалить. В новом массиве все значения должны быть уникальными.

3. 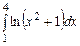, , 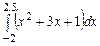, 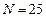метод трапеций

Вариант 16

1. Отсортировать массивы М₁ (20), М₂ (18) и вторую половину массива М₃ (26) в порядке возрастания.

2. Вычислить 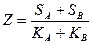, где S_A, K_A, S_B, K_B – суммы и количества положительных элементов массивов А (75) и В (60) соответственно.

3. 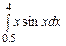, , 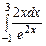, 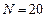метод парабол

Вариант 17

1. Отсортировать элементы нечетных строк матрицы А (6х7) в порядке убывания, а четных – в порядке возрастания. Определить функцию сортировки последовательности, направление сортировки передавать параметром.

2. Даны матрицы В (m,n) и С (n,m). Определить, есть ли в заданных матрицах столбцы, содержащие по два отрицательных элемента. Вывести номера таких столбцов. Описать функцию для анализа одного столбца.

3. 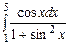, , 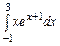, 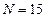метод Ньютона

Вариант 18

1. Даны матрицы В (m,n) и С (n,m). Определить, есть ли в заданных матрицах строки, содержащие равное число положительных и отрицательных элементов. Вывести номера таких строк.

2. Дан целочисленный массив А из 10n элементов (n <=10). В каждой десятке найти наименьшее значение и вывести ту часть массива, где минимум больше. Для ввода, вывода массива и поиска минимума в одной части массива использовать функции.

3. 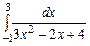, , 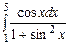, 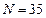метод трапеций

Вариант 19

1. Удалить из матриц G (6х8) и D (5х7) столбцы, содержащие хотя бы один нулевой элемент, передвинув на их место следующие столбцы без на­рушения порядка их следования.

2. Подсчитать количество элементов матрицы Р (10х12), отличающихся от среднего арифметического значения элементов массива М (100) более чем вдвое, и количество элементов массива М, отличающихся от среднего арифметического значения матрицы Р более, чем втрое.

3. 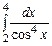, , 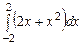, 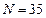метод трапеций

Вариант 20

1. Подсчитать количество элементов массива Р (40), отличающихся от среднего арифметического значения элементов матрицы М (6х9) не более чем на два, и количество элементов матрицы М, отличающихся от среднего арифметического значения массива Р не более, чем на три.

2. Заменить минимальный элемент массива А (5х8) максимальным элементом массива В (7х6), а минимум массива В – максимальным элементом массива А. Массивы, в которых минимальное или максимальное значение встречается неоднократно, считать некорректными.

3. 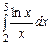, , 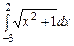, 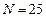метод прямоугольников

Вариант 21 *

1. Без нулей. Для заданного натурального числа N найти наименьшее основание p системы счисления, в которой представление числа N не содержит нулей. Напечатать это представление.

2. Замочная скважина. Даны мозаичные изображения замочной скважины и ключа. Пройдет ли ключ в скважину? То есть даны матрицы L (M_lxN_l) и K (M_kxN_k), где M_l>M_k и N_l>N_k состоящие из нулей и единиц. Проверить, можно ли наложить матрицу K на матрицу L так, чтобы каждой единице матрицы K соответствовал нуль в матрице L (без поворота, разрешается только сдвиг). Если можно, то как (на сколько и в каком направлении следует подвинуть матрицу K по матрице L до выполнения условия)? Если нельзя, то проверить возможность наложения, когда «ключ» разрешается поворачивать на угол, кратный 90°.

Вариант 22 *

1. Перетекание массы. На плоскости заданы п материальных точек. С некоторого момента точка с наименьшей массой исчезает, передавая свою массу ближайшей к ней точке. Так продолжается до тех пор, пока не останется одна точка. Реализовать этот процесс и найти оставшуюся точку.

2. Симметрия. Описать рекурсивную логическую функцию, которая проверяет, является ли симметричной часть заданного массива F (40), начинающаяся i-м и кончающаяся j-м элементами.

Контрольные вопросы

1. Что такое функция?

2. Что такое прототип функции?

3. Чем отличается прототип функции от вызова функции?

4. Чем отличается описание функции от определения функции?

5. Критерии соответствия формальных и фактических параметров.

6. Соответствие типов формальных и фактических параметров.

7. Когда при объявлении функции используется слово void?

8. Зачем нужен оператор return?

9. Может ли в функции быть несколько операторов return?