2. Какой объем памяти занимает указатель?
3. Что является значением переменной-указателя?
4. Как проинициализировать указатель?
5. Что такое NULL?
6. Что такое указатель на void? Зачем нужны такие указатели?
7. Какие операции допустимы при работе с указателями?
8. Чем отличается унарная операция "&" от унарной "*" ?
9. Совместимость типов указателей.
10. Можно ли получить адрес указателя?
11. Можно ли указателю присвоить его же адрес?
12. Почему к указателю на void нельзя применить операцию разыменования?
13. Как работают операции инкремента и декремента, примененные к указателям?
14. Каков результат операции вычитания, примененной к указателям одного типа?
15. Какой спецификатор типа используется при выводе адреса на экран с помощью функции printf()?
16. В чем отличие записи ( double *) a от ( double ) * a, если а – указатель на целое число?
17. В чем отличие записи *а++ от (*а)++, если а – некоторый указатель, отличный от void*?
18. Как описать указатель на начало массива?
19. Как описать указатель на указатель?
20. Когда и зачем может повторно использоваться операция разыменования?
Практическая работа № 4.
Массивы. Динамическое выделение памяти
Цель работы – познакомиться с организацией массивов в языке Си, изучить принципы работы с массивами, освоить работу с массивами через указатели, научиться грамотно выделять и освобождать память в процессе работы программы.
Функции для работы с динамической памятью
Выделение памяти
void * malloc (size_t size);
возвращает указатель на место в памяти для объекта размера size или, если памяти запрашиваемого объема нет, NULL. Выделенная область памяти не инициализируется.
void * calloc (size_t nobj, size_t size);
возвращает указатель на место в памяти, отведенное для массива nobj объектов, каждый из которых размера size, или, если памяти запрашиваемого объема нет, NULL. Выделенная область памяти обнуляется.
void * realloc (void *p, size_t size);
заменяет на size размер объекта, на который указывает p. Для части, размер которой равен наименьшему из старого и нового размеров, содержимое не изменяется. Если новый размер больше старого, дополнительное пространство не инициализируется. Функция realloc возвращает указатель на новое место памяти или, если требования не могут быть удовлетворены, NULL (*p при этом не изменяется).
Освобождение памяти
void free (void *р);
Постановка задачи
Написать шесть программ согласно индивидуальному варианту. Использовать обращение к элементам массива с помощью операции индексации и через указатель. Ввод элементов массива осуществлять с клавиатуры, контролировать корректность ввода. Во время отладки и тестирования программы размер массива можно уменьшить. При выводе матриц следить за тем, чтобы ширина всех столбцов матрицы была одинаковой.
Во второй задаче память под массив выделять динамически.
Одну из задач с матрицей (третью или четвертую) решить двумя способами:
1) матрицу записать в виде статического двумерного массива;
2) организовать динамическую матрицу, используя динамическое выделение памяти.
Варианты заданий
Вариант 1
1. Определить, представляют ли собой элементы массива А (20) возрастающую последовательность.
2. Сформировать новый массив из элементов исходного линейного массива, встречающихся в нем только один раз.
3. Вычислить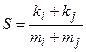 
, где ki и kj – индексы строки и столбца минимального положительного элемента матрицы Y (5х7), а mi и mj– индексы строки и столбца первого положительного элемента.
4. Определить, является ли данная квадратная матрица симметричной относительно своей побочной диагонали.
5. Книга – трехмерный массив букв (3 координаты – страница, строка, номер буквы в строке). Вывести на экран n-ю строку со страницы p книги, содержащей 450 страниц, на каждой странице которой размещается по 80 строк, длина каждой строки – 64 символа.
Вариант 2
1. Записать элементы массива С (20) в обратном порядке {С20;С19;С18;…;С2;С1}. Вспомогательный массив не использовать.
2. Определить количество элементов линейного массива, больших среднего арифметического значения элементов этого массива.
3. Заполнить матрицу А (8х8) следующим образом: на главной диагонали – «0», над диагональю – «1», под диагональю – «-1».
4. Поменять местами минимальный элемент целочисленной матрицы Р (9х11) и элемент, значение которого совпадает с заданным X. Если указанный элемент в матрице отсутствует, вывести сообщение об этом. Матрица, в которой минимальное значение встречается неоднократно, является некорректной.
5. Куб состоит из n3 прозрачных и непрозрачных элементарных кубиков. Построить полностью непрозрачный куб, используя ровно n2 непрозрачных элементарных кубиков.
Вариант 3
1. В массиве А (45) найти локальные максимумы, определить их местоположение. Локальным максимумом назовем элемент массива, значение которого больше, чем значения двух соседних с ним элементов. Крайние элементы массива являются локальными максимумами, если они больше единственного соседнего элемента.
2. Удалить из целочисленного одномерного массива все элементы, значения которых в этом массиве повторяются, оставив по одному.
3. Дана матрица размером 7х7. Поменять местами k-й столбец с k-ой строкой (первый элемент k–го столбца меняется с первым элементом k–й строки, второй со вторым и так далее). Значение k вводится с клавиатуры.
4. Вычислить среднее арифметическое значение элементов, лежащих на диагоналях квадратной матрицы. Заменить этим значением все элементы матрицы, не лежащие на диагоналях.
5. Трехмерный массив описывает журнал фиксации среднесуточной температуры в течение 10 календарных лет. Каждая страница журнала описывает один год, номера строк соответствуют месяцам года, а номера столбцов – дням месяца (считать, что в каждом месяце 30 дней). Определить самый жаркий и самый холодный дни в каждом календарном году и за весь период наблюдения (указать даты и температуру воздуха).
Вариант 4
1. Из элементов массивов А (20) и С (20) образовать новый массив Х={a1,c1,a2,c2,…,a20,c20}
2. Вычислить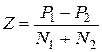 
, где P1 и P2 – первый и второй положительные элементы линейного массива, N1 и N2 – первый и второй отрицательные элементы того же массива. Массивы, в которых нет хотя бы двух положительных и двух отрицательных элементов, являются некорректными.
3. Поменять местами максимальный и минимальный элементы матрицы А (8х12). Если в массиве максимальное или минимальное значение встречается неоднократно, данный массив признается некорректным.
4. Вычислить среднее арифметическое значение элементов, лежащих на диагоналях квадратной матрицы. Заменить этим значением все диагональные элементы матрицы.
5. Результаты сессии, состоящей из четырех экзаменов, для трех групп из 25 студентов представлены трехмерным массивом 3х25х4. Оценка ставится по четырехбалльной системе; неявка обозначена единицей. Определить, экзамен по какой дисциплине вызвал наибольшие трудности, то есть по какой дисциплине средний балл наименьший.
Вариант 5
1. В массиве А (27) наименьший элемент поместить на первое место, наименьший из оставшихся – на последнее место, следующий по величине – на второе место, следующий – на предпоследнее и так далее до середины массива. Все элементы массива должны различаться.
2. Вставить число 100 после второго положительного элемента линейного массива, сдвинув оставшиеся элементы к концу массива. Учесть изменение размера массива. Массив, в котором нет двух положительных элементов, признается некорректным.
3. Вычислить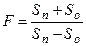 
, где Sn – сумма положительных элементов в нечетных строках матрицы Y (9х12), а So – сумма отрицательных элементов в четных строках той же матрицы.
4. Дана матрица А (10х10). Отсортировать элементы, лежащие на главной диагонали, в порядке возрастания.
5. Трехмерный массив описывает журнал преподавателя. Каждая страница журнала содержит отметки о степени выполнения N студентами одной группы М лабораторных работ (в каждой строке – отметки одного студента, в каждой колонке – отметки по одной работе). Всего существует 5 степеней выполнения работы: 0 – ничего, 1 – получено задание, 2 – выполнена работа, 3 – сформирован отчет о работе, 4 – работа защищена. В журнале L страниц – по количеству студенческих групп. Пусть N=25, M=7, L=8. Подсчитать, сколько студентов будет допущено к экзамену в каждой группе и сколько из них получат экзамен «автоматом». К экзамену допускаются студенты, у которых есть отчеты по всем лабораторным работам. «Автоматом» проставляется экзаменационная оценка студентам, защитившим все работы.
Вариант 6
1. Преобразовать заданный массив следующим образом: из положительных элементов вычесть первый, к отрицательным прибавить последний элемент, первый и последний элементы, а также равные 0 оставить без изменений.
2. Вставить после каждого пятого элемента линейного массива значение, равное сумме трех предшествующих элементов. Количество элементов в массиве после вставки должно увеличиться.