5. Составить программу для определения, является ли натуральное число k степенью числа 3.
6. Первоначальный объем древесины на участке леса составляет р кубометров. Ежегодный прирост составляет k%. Годовой план заготовки составляет t кубометров. Определить, через сколько лет в этом лесу будут расти одни опята?
7. Вычислить значение суммы бесконечного ряда с заданной точностью e=10-5,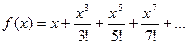 
и значение функции (для проверки) 
.
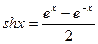8. Вычислить значение суммы бесконечного ряда с заданной точностью e=10-4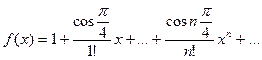 
, и значение функции (для проверки) 
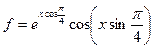, учесть, что 
.
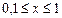9. Дано натуральное N. Вычислить сумму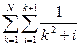 
Вариант 17
1. 
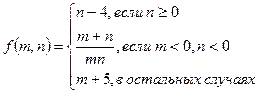
2. 
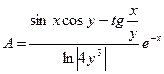
3. Определить, лежат ли три точки с координатами (x1, y1), (x2, y2), (x3, y3) на одной прямой. Если не лежат, то вычислить расстояния до каждой точки из начала координат. Если лежат, то получить общее уравнение этой прямой вида Ax + By + C=0, где A³0.
4. Получить таблицу температур по Цельсию от 0° до 100° и их эквивалентов по шкале Фаренгейта, используя для перевода формулу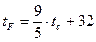 
.
5. Вычислить сумму кубов всех четных чисел, лежащих в диапазоне [X, Y], где X и Y – вводимые с клавиатуры натуральные числа.
6. С клавиатуры вводится число N. Определить, может ли оно быть двоичным (т.е. состоять только из 0 и 1).
7. Вычислить значение суммы бесконечного ряда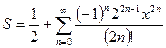 
с заданной точностью e=10-6 и значение функции (для проверки) y=cos2x.
8. Вычислить значение суммы бесконечного ряда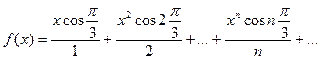 
с заданной точностью e=10-6, и значение функции (для проверки) 
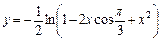учесть, что 
.
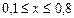9. Дано целое число а. Найти все такие простые числа p, что дробь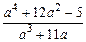 
сократима на p. Простым называется натуральное число N, не имеющее других делителей, кроме 1 и самого N.
Вариант 18
1. 
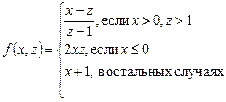
2. 
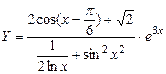
3. Для заданного натурального а (а<140), рассматриваемого как возраст человека, вывести фразу вида: «Мне 21 год», «Мне 32 года», «Мне 12 лет».
4. Написать программу вычисления значения выражения при заданных х и n: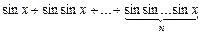 
.
5. С клавиатуры вводится последовательность чисел, найти максимальное из них. Признак окончания ввода – ввод 0 (в вычислениях не участвует).
6. Определить, является ли сумма цифр натурального числа N четной.
7. Вычислить значение суммы бесконечного ряда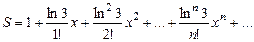 
с точностью до члена ряда, по модулю меньшего e=10-6 , и значение функции (для проверки) f=3x, учесть, что 0£x£1.
8. Вычислить значение суммы бесконечного ряда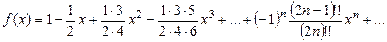 
с заданной точностью e=10-5 и значение функции (для проверки) 
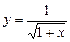, учесть, что x2<1.
9. Дано k натуральных чисел. Определить сколько из них совершенных. Совершенным называется число, равное сумме всех своих делителей, включая 1 и не включая само число.
Вариант 19
1. 
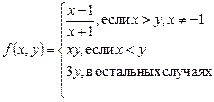
2. 
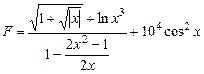
3. Даны три числа: a, b и c. Определить, есть ли среди них одинаковые по модулю. Если все значения по модулю различны, то поменять знак у каждого из них. Если все значения одинаковые по модулю, то возвести их в квадрат. Если найдется одна пара одинаковых по модулю значений, то большие по модулю значения удвоить, а меньшие – утроить.
4. Найти все двузначные числа, квадраты которых оканчиваются на три одинаковые цифры, отличные от нуля.
5. Даны два натуральных числа X и Y. Составить программу для вычисления суммы кубов всех четных чисел, лежащих в диапазоне [X, Y].
6. С клавиатуры вводится число N. Определить, может ли оно быть восьмеричным (т.е. состоять только из цифр меньше 8).
7. Вычислить значение суммы бесконечного ряда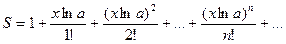 
с точностью до члена ряда, меньшего
e=10-4, и значение функции (для проверки) f=ax, учесть, что 0,1£ x £1.
8. Вычислить значение суммы бесконечного ряда с заданной точностью e=10-5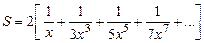 
и значение функции (для проверки) 
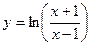, учесть, что |x|>1.
9. Последовательность a1,a2,a3,.. образована по закону а1= b , ai = ai -1-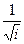 
, i =2,3,…. Найти первый отрицательный член последовательности для различных b =3,4,5,6,7,8,9.
Вариант 20
1. 
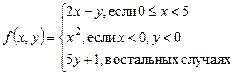
2. 
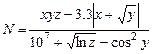
3. Определить вид треугольника (прямоугольный, остроугольный или тупоугольный), зная длины его сторон. Если треугольник прямоугольный, то найти величины его острых углов, если он остроугольный, то найти его периметр, а в противном случае найти его наибольшую сторону.
4. Составить программу для определения наименьшего среди чисел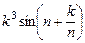 
, (k=1, 2, …, n). Значение n вводится с клавиатуры.
5. Определить, является ли данное натуральное число N факториалом какого-нибудь числа, если «да», то какого. Число N будет являться факториалом числа n (обозначается n!), если его значение равно произведению чисел натурального ряда от 1 до n, например 120=1·2·3·4·5=5!, т.е. 120 является факториалом числа 5.
6. Найти все шестизначные числа, которые увеличиваются втрое при перестановке первой цифры числа в конец.
7. Вычислить значение суммы бесконечного ряда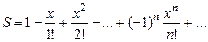 
с точностью до члена ряда, по модулю меньшего e=10-4, и значение функции (для проверки) f=e-x .
8. Вычислить значение суммы бесконечного ряда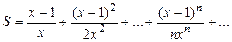 
с точностью до члена ряда, меньшего e=10-5, и значение функции (для проверки) f=lnx, учесть x>1.
9. Последовательно вводятся n натуральных чисел(n £10). Вычислить сумму тех из них, у которых первая цифра равна последней.
Контрольные вопросы
1. Чем отличается условная операция от условного оператора?
2. Что такое полная и неполная форма условного оператора?
3. Может ли существовать неполная форма условной операции?