Определяем строки с номерами, совпадающими с номерами помеченных столбцов. Отыскиваем , находящиеся в непомеченных столбцах, и присваиваем им номера просматриваемых строк. И так далее.
ПЛАН ЗАНЯТИЯ
Дисциплина: ОП.10 Математические методы
Преподаватель: Старченко Е.А
Курс: 3
Группа: 1 ПКС-20
Специальность: Программирование в компьютерных системах
Дата: 21.12.22
Время проведения: 13.30 – 15.00, 4 пара
Вид занятия практическое занятие
Литература
Ходыкин В.Ф., ПреображенскийА.А. Сборник задач по математическому программированию
Интернет-ресурсы:
видео https://youtu.be/GxAUU_oQ8fE
Задание: выполнить задание, ответы в электронном варианте отправить для проверки.
Лабораторная работа №15
Тема: Максимальный поток на графе.
Цель: Научиться применять алгоритм Форда для нахождения максимального потока на графе.
Оборудование: ручка, карандаш, лист А4.
Ход работы
1. Инструктаж по ТБ.
2. Теоретические сведения.
Алгоритм Форда состоит из ряда шагов.
Предварительный шаг.
Строим квадратную таблицу с количеством строк и столбцов, равным числу вершин. На пересечении строк и столбцов заносим пропускные способности дуг. Если пропускная способность дуги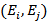 
больше нуля, а симметричной ей – равна нулю, то в клетку 
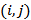заносим 
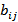, а в клетку 
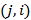– нуль; если 
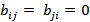, то соответствующие клетки не заполняются.
Общий шаг.
Данный шаг включает три этапа.
1-й этап. Определяем путь из источника в сток, у которого пропускная способность больше нуля. Столбец, соответствующий вершине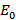 
, помечаем * (звёздочкой)ю Данная пометка символизирует запрет на возврат в вершину 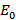при движении от источника к стоку. Двигаясь по строке 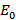, находим 
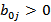и помечаем соответствующие им столбцы цифрой 0 (по номеру строки). Таким образом, определяются первые дуги пути из 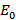в 
.
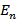Определяем строки с номерами, совпадающими с номерами помеченных столбцов. Отыскиваем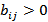 
, находящиеся в непомеченных столбцах, и присваиваем им номера просматриваемых строк. И так далее.
На данном этапе возможны два случая:
1) помечен столбец 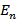(сток). Это означает, что имеется путь с пропускной способностью, отличной от нуля;
2) в просматриваемых строках нет непомеченных столбцов с 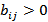, но 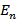не помечен. Следовательно, отсутствует путь из 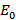в 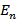с положительной пропускной способностью.
Определим путь для первого случая.
Пусть последняя вершина пути 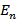помечена номером 
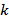. Следовательно, последняя дуга пути – 
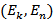. Элементу 
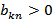, стоящему на пересечении 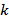– ой строки и 
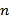– го столбца, ставим в соответствие знак «-», а симметричному ему 
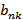– знак «+».
| * | 0 | f | r | k | ||
|
| 
| … | 
| 
|
| |
|
| 
| … | ||||
|
| 
| … | ||||
| … | … | … | … | … | … | … |
|
| … | 
| ||||
|
| … | 
| 
| |||
|
| … | 
|
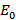
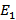
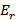
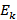
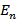
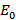
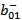
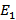
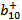
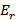
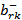
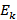
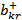
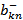
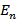
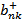
Рассмотренная 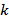-ая строка была взята на основании того, что перед этим был помечен 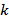-ый столбец. Пусть он был помечен номером 
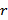. Двигаемся от величины
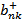по -ому столбцу до строки 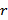. (Предпоследняя дуга пути - 
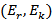), далее, до тех пор, пока не дойдём до 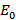- ой строки. Элемент 
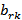отмечаем знаком «-», а симметричный ему 
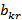– знаком «+». Переходим к действию 2.
Рассмотрим второй случай.
Пусть пути с пропускной способностью, отличной от нуля, больше нет (имеется в виду в каком-то общем шаге, но не на первом). Вершины, находящиеся в помеченных столбцах, образуют подмножество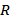 
(они достижимы), остальные вершины в подмножество 
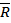. Дуги, для которых 
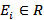и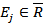 
, образуют разрез с минимальной пропускной способностью
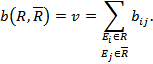
2-й этап. Определяем пропускную способность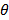 
найденного пути 
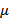. Она определяется из выражения
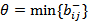
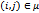
3-й этап. Определяем остаточные пропускные способности дуг найденного пути и симметричных к ним. Для этого выполняем действия
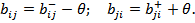
Получаем таблицу с новыми пропускными способностями.
Возвращаемся к действию 1 и производим вычисления до тех пор, пока не получим таблицу, в которой нет ни одного пути из 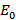в 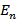с пропускной способностью больше нуля.
После этого переходим к заключительному шагу алгоритма.
Заключительный шаг.
Находим разности между соответствующими элементами исходной таблицы и полученной на последнем шаге. Получаем таблицу, в которой положительные элементы равны искомым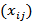 
– величинам потоков, движущимся по дугам 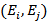. Максимальный поток равен либо сумме элементов 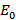- й строки, либо 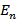- го столбца
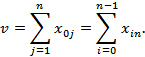
Величина потока, перемещаемого по сети, может также быть определена как сумма пропускных способностей найденных путей, либо, после выделения дуг разреза, как сумма пропускных способностей данных дуг.
3. Задание.
Для приведённой сети (рис. 1) найти величину максимального потока из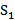 
в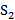 
. Пропускные способности дуг и рёбер заданы на рисунке 1.
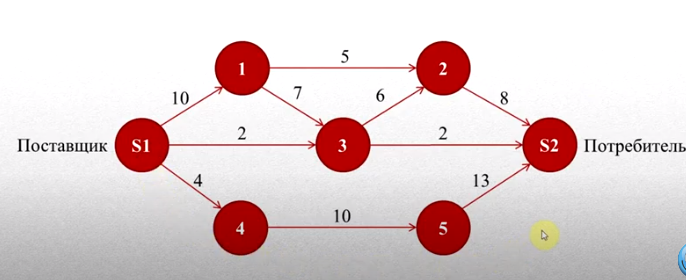
Рис. 1
Контрольные вопросы.
1. Сколько шагов включает в себя алгоритм Форда? Перечислите их.
2. Какие случаи возможны на 1 этапе общего шага? В чём суть 2 и 3?
3. Какие действия выполняются на предварительном и заключительном шагах?