4. Дано натуральное n и вещественное x. Вычислить сумму n слагаемых
5. Дано натуральное число N. Выяснить, является ли оно степенью числа 5.
6. Известно время начала и окончания (например, 6:00 и 24:00) работы некоторого пригородного автобусного маршрута с одним автобусом на линии, а также протяженность маршрута в минутах (в один конец) и время отдыха на конечных остановках. Составить суточное расписание этого маршрута (моменты отправления с конечных пунктов) без учета времени на обед и пересменку.
7. Вычислить значение суммы бесконечного ряда с заданной точностью e=10-6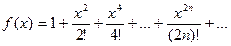 
, и значение функции (для проверки) 
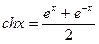, учесть, что 0,1£x£1.
8. Вычислить значение суммы бесконечного ряда с заданной точностью e=10-5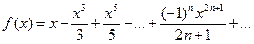 
и значение функции (для проверки) f=arctg(x), учесть, что x2<1.
9. Дано положительное число k. Для каждого значения x =2,3,4,…,8 найти такое наименьшее целое n, при котором xn превышает заданное k.
Вариант 14
1. 
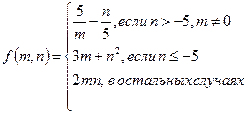
2. 
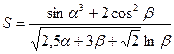
3. В финале шашечной партии остались белая дамка и две черных пешки, позиции которых известны. Ход белых. Сможет ли дамка срубить хотя бы одну пешку?
4. Составить программу для определения, в каких двузначных числах удвоенная сумма цифр равна их произведению.
5. Несколько деталей должны последовательно пройти обработку на каждом из трех станков. Продолжительности обработки каждой детали на каждом станке вводятся группами по 3 числа до исчерпания ввода (признак окончания ввода – задание некорректной тройки чисел). Сколько времени займет обработка всех деталей, если на каждом станке детали могут обрабатываться только поштучно?
6. Получить число, образованное записью цифр исходного числа N в обратном порядке.
7. Вычислить значение суммы бесконечного ряда с заданной точностью e=10-5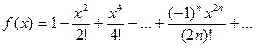 
и значение функции (для проверки) y=cosx.
8. Вычислить значение суммы членов бесконечного ряда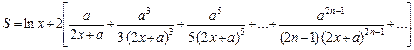 
с точностью до члена ряда, меньшего e=10-4 для a2<(2x+a)2 и значение функции (для проверки) f = ln ( x + a ).
9. Вычислить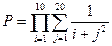 
(произведение 10 сомножителей, каждое из которых является суммой 20 дробей).
Вариант 15
1. 
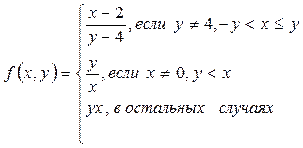
2. 
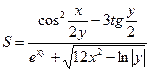
3. На шахматной доске стоят черный король и белые ладья и слон (ладья бьет по горизонтали и вертикали, слон – по диагоналям). Проверить, есть ли угроза королю и если есть, то от кого именно. Учесть возможность защиты (например, ладья не бьет через слона).
4. Найти все трехзначные числа, сумма цифр которых кратна 7 и само число также делится на 7.
5. Определить, являются ли натуральные числа a и b взаимно простыми. Взаимно простые числа не имеют общих делителей, кроме единицы.
6. Можно ехать на такси со скоростью v 1 км/ч и оплатой m р/км или идти пешком со скоростью v 2 км/ч бесплатно. Как с наименьшими финансовыми затратами преодолеть путь S за время t, если это возможно? Каковы эти затраты?
7. Вычислить значение суммы бесконечного ряда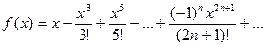 
с заданной точностью e=10-5 и значение функции (для проверки) y=sinx.
8. Вычислить значение суммы бесконечного ряда с заданной точностью e=10-6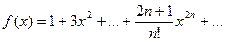 
, и значение функции (для проверки) 
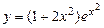, учесть, что 
.
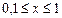9. Вычислить сумму s=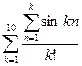 
.
Вариант 16
1. 
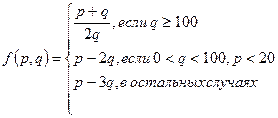
2. 
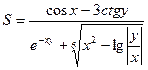
3. Определить, лежат ли две точки с координатами (x1, y1) и (x2, y2) в одной четверти. Если лежат, то вычислить периметр треугольника, вершинами которого являются начало координат и данные точки, если все точки лежат на одной прямой, то вывести сообщение об этом. Если точки в одной четверти не лежат, то определить, лежат ли они в одной полуплоскости.
4. Ввести натуральное число N. Определить, является ли оно совершенным (совершенное число N равно сумме всех своих делителей, включая 1 и не включая само N).