4. Дано натуральное число N. Вычислить произведение .
5. Даны натуральные числа a и b (a и b должны быть больше 10). Определить все числа, кратные a и b, меньшие произведения a·b.
6. Факториал некоторого числа равен p. Найти это число. Число p будет являться факториалом числа n (обозначается n!), если его значение равно произведению чисел натурального ряда от 1 до n, например 120=1·2·3·4·5=5!, т.е. 120 является факториалом числа 5.
7. Вычислить значение суммы бесконечного ряда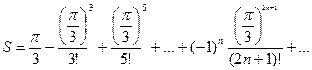 
с заданной точностью e=10-6 и значение функции (для проверки) f=sin 
.
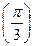8. Вычислить значение суммы бесконечного ряда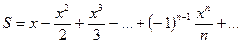 
с заданной точностью e=10-6 и значение функции (для проверки) f=ln(1+x), учесть -1<x£1
9. Даны натуральные числа а, b (а<b). Получить все простые числа p, удовлетворяющие неравенству a<p<b. Простыми называются числа, не имеющие других делителей, кроме 1 и самого себя.
Вариант 10
1. 
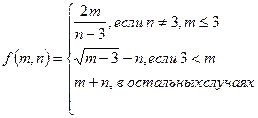
2. 
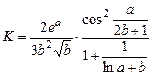
3. Написать программу для решения неравенства ax+b>0 относительно x для любых значений a и b.
4. Для натурального числа n получить все его натуральные нечетные делители.
5. Определить наибольшее число, факториал которого не превышает 105. Факториал числа n (обозначается n!) равен произведению чисел натурального ряда от 1 до n, например 5! =1·2·3·4·5=120.
6. Получить число, образованное записью цифр исходного числа N в обратном порядке.
7. Вычислить значение суммы бесконечного ряда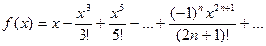 
с заданной точностью e=10-5 и значение функции (для проверки) y=sinx.
8. Вычислить значение суммы бесконечного ряда с заданной точностью e=10-5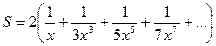 
и значение функции (для проверки) 
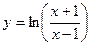, учесть, что |x|>1.
9. Дано натуральное число n. Вычислить S=1+22+33+…+nn. Функцию возведения в степень не использовать.
Вариант 11
1. 
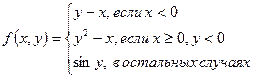
2. 
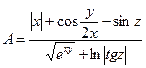
3. Даны три целых числа: K, M и N. Определить, сколько среди заданных чисел четных. Если ни одного, то каждое число возвести в квадрат, если одно, то увеличить его на 1, если два, то нечетное удвоить. Если все числа четные, изменять их не требуется.
4. Составить программу для вычисления значения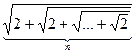 
при заданном значении n.
5. Перевести число из десятичной системы счисления в восьмеричную т. е. получить число, являющееся восьмеричной записью числа n.
6. Определить, сколько раз в написании введенного с клавиатуры натурального числа встречается цифра 2.
7. Вычислить значение суммы бесконечного ряда 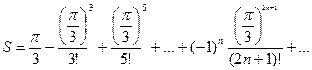с заданной точностью e=10-6 и значение функции (для проверки) f=sin .
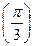8. Вычислить значение суммы бесконечного ряда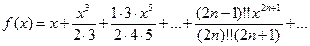 
с заданной точностью e=10-5 и значение функции (для проверки) f(х)=arcsinx, учесть, что 0,05 ≤ x ≤ 1.
9. Утверждается, что разность любого натурального числа и суммы его цифр кратна 9. Проверить этот факт для всех чисел, лежащих между заданными m и n .
Вариант 12
1. 
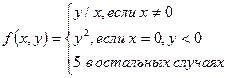
2. 
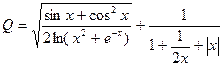
3. Точки с координатами (x1, y1) и (x2, y2) являются концами отрезка. Определить, пересекает ли этот отрезок график функции F(x)=х. Если пересекает, то найти расстояние от каждой точки до данной прямой. Если не пересекает, то определить, принадлежит ли этот отрезок прямой, параллельной данной, или прямой, ей перпендикулярной.
4. Дано натуральное число n. Вычислить F=1!+2!+…+n ! Факториал числа n равен произведению чисел натурального ряда от 1 до n.
5. Вывести на экран значение первого отрицательного члена последовательности cos ( ctg ( n )), n =1,2,3,…. Отрицательные члены в этой последовательности обязательно есть.
6. Предприниматель, начав дело, взял кредит размером k рублей под р процентов годовых и вложил его в свое дело. По прогнозам, его дело должно давать прибыль r рублей в год. Сможет ли он накопить сумму, достаточную для погашения кредита, и если да, то через сколько лет?
7. Вычислить значение суммы бесконечного ряда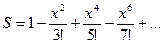 
с точностью до члена ряда, по модулю меньшего e=10-5, и значение функции (для проверки) 
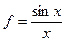, учесть, что -π£ x £ π.
8. Вычислить значение суммы бесконечного ряда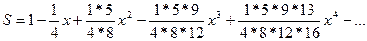 
с точностью до члена ряда, по модулю меньшего e=10-4 , и значение функции (для проверки) f =(1+ x)-1/4, учесть, что x2<1.
9. Найти все натуральные числа, не превосходящие заданного n, десятичная запись которых есть строго возрастающая или строго убывающая последовательность цифр.
Вариант 13
1. 
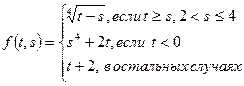
2. 
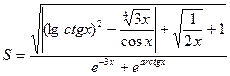
3. Дано натуральное трехзначное число. Если все цифры в нем различны, то оставить заданное число без изменения; если все цифры в нем одинаковые, то первую уменьшить на 1, а последнюю, если это не 9, увеличить на 1; если две цифры в числе одинаковые, то получить число с обратным порядком цифр.