5. Дано натуральное n. Составить программу для поиска первой цифры этого числа.
6. Перевести заданное натуральное число n из десятичной системы счисления в двоичную, т. е. получить число, являющееся двоичной записью числа n.
7. Вычислить значение суммы бесконечного ряда с заданной точностью e=10-6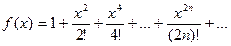 
, и значение функции (для проверки) 
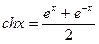, учесть, что 0,1£x£1.
8. Вычислить значение суммы бесконечного ряда с заданной точностью e=10-4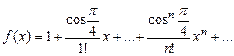 
, и значение функции (для проверки) 
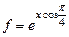, учесть, что 0,1£x£1.
9. Последовательно вводятся целые положительные числа. Признаком конца ввода является ввод нуля. Для каждого числа выяснить, является ли оно факториалом какого либо числа. Если да, то вывести число, факториалом которого является введенное, если нет, то вывести сообщение об этом. Число будет являться факториалом числа n (обозначается n!), если его значение равно произведению чисел натурального ряда от 1 до n, например 120=1·2·3·4·5=5!, т.е. 120 является факториалом числа 5.
Вариант 8
1. 
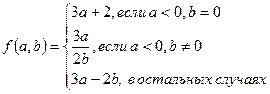
2. 
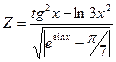
3. Даны стороны треугольника. Определить его вид: равносторонний, равнобедренный или разносторонний,– и вывести сообщение об этом. Кроме того, если треугольник равносторонний, то найти его площадь, если он равнобедренный, то найти его периметр, а в противном случае найти его наименьшую сторону.
4. Исходное данное – натуральное число K, выражающее площадь. Написать программу для нахождения всех таких прямоугольников, площадь которых равна K и стороны выражены натуральными числами.
5. Спортсмен в первый день пробежал 10 км. Каждый следующий день он увеличивал дневную норму на 10% от предыдущего дня. Через сколько дней спортсмен будет пробегать в день больше 20 км?
6. Определить, является ли данное натуральное число N палиндромом (палиндром слева направо и справа налево читается одинаково, например 32423).
7. Вычислить значение суммы бесконечного ряда с заданной точностью e=10-5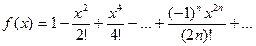 
и значение функции (для проверки) y=cosx.
8. Вычислить значение суммы бесконечного ряда с заданной точностью e=10-4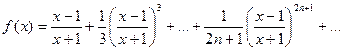 
, и значение функции (для проверки) 
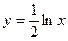, учесть, что 
.
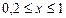9. Найти натуральное число в диапазоне от 2 до n (n£100) с максимальной суммой делителей (само число в сумму не включать).
Вариант 9
1. 
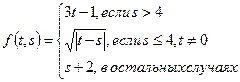
2. 
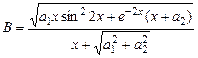
3. Дано натуральное трехзначное число. Если все цифры в нем одинаковы, то оставить заданное число без изменения; если все цифры в нем разные, то меньшую из них заменить в заданном числе нулём; если две цифры в числе одинаковые, то получить число с обратным порядком цифр.