6. Дано натуральное число n. Составить программу для определения количества цифр в этом числе.
7. Вычислить значение суммы бесконечного ряда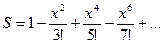 
с точностью до члена ряда, по модулю меньшего e=10-5, и значение функции (для проверки) 
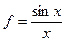, учесть, что -π£ x £ π.
8. Вычислить значение суммы бесконечного ряда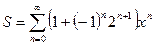 
с точностью до члена ряда, по модулю меньшего e=10-4, и значение функции (для проверки) 
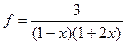, учесть, что |x|<0,5.
9. Написать программу для поиска 100 первых простых чисел. Простыми называются натуральные числа, не имеющие других делителей, кроме 1 и самого числа.
Вариант 5
1. 
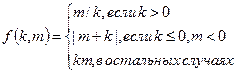
2. 
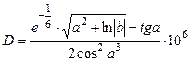
3. Даны координаты двух точек на плоскости. Если хотя бы одна из них лежит на какой-нибудь оси, то вывести сообщение об этом; если они обе находятся в одной четверти, то найти расстояние между ними; иначе найти точку, наиболее удаленную от центра координат.
4. Вычислить a(a-n)(a-2n)…(a-n2). Вещественное а и натуральное n вводятся с клавиатуры.
5. Вычислить, за сколько лет в банке при начальном вкладе W и процентах годового прироста Pr будет накоплена сумма Sum (проценты капитализируются ежегодно).
6. Определить, содержится ли в десятичной записи натурального числа N цифра 3.
7. Вычислить значение суммы бесконечного ряда с заданной точностью e=10-5,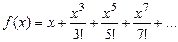 
, и значение функции (для проверки) 
.
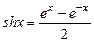8. Вычислить значение суммы бесконечного ряда с заданной точностью e=10-4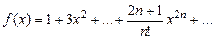 
, и значение функции (для проверки) 
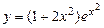, учесть, что 
.
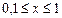9. Последовательно вводятся n натуральных чисел(n £ 10). Вычислить сумму тех из них, у которых первая цифра равна последней.
Вариант 6
1. 
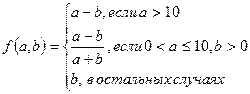
2. 
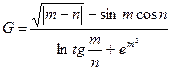
3. Даны три целых числа. Если среди них есть ноль, то все числа обнулить. Если два числа положительны, а третье отрицательно, то отрицательное возвести в квадрат. Если два числа отрицательны, а третье положительно, то сменить знак у каждого числа. Если все числа имеют один знак, то изменять их не требуется.
4. У гусей и кроликов вместе 2N лап. Сколько может быть гусей и кроликов (вывести все возможные сочетания)?
5. Дано целое m >1. Получить наибольшее целое k, при котором 4k<m.
6. Найти число Фибоначчи, ближайшее к заданному натуральному числу n. Каждый член последовательности Фибоначчи является суммой двух предыдущих xn=xn-1+xn-2, x0=0, x1=1.
7. Вычислить значение суммы бесконечного ряда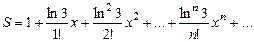 
, с точностью до члена ряда, по модулю меньшего e=10-4 , и значение функции (для проверки) f=3x, учесть, что 0£x£1.
8. Вычислить значение суммы бесконечного ряда с заданной точностью e=10-5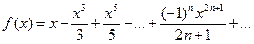 
и значение функции (для проверки) f=arctg(x), учесть, что x2<1.
9. Дано k натуральных чисел. Определить сколько из них совершенны. Совершенным называется число, равное сумме всех своих делителей, включая 1 и не включая само число.
Вариант 7
1. 
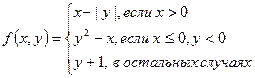
2. 
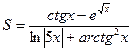
3. Даны два числа. Если они оба отрицательны, то первое уменьшить на 1, а второе увеличить на 1; если оба положительны, то большее из них удвоить, а меньшее утроить; если знаки чисел различны, то отрицательное число заменить его абсолютным значением. Если хотя бы одно из чисел равно нулю, то изменять их не требуется.
4. Дано натуральное число n>10 и вещественное х. Составить программу для вычисления значения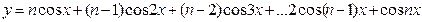 
.