4. Дано натуральное n. Вычислить n сомножителей произведения .

Дата: 2025-05-25; Просмотры: 3
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

5. Представить натуральное число N в виде произведения простых сомножителей. Простыми называются сомножители, которые нельзя в свою очередь разложить на сомножители.

6. Поменять местами цифры старшего и младшего разрядов данного натурального числа (например, из числа 3872 получится 2873).

7. Вычислить значение суммы бесконечного ряда 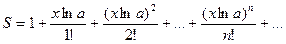с точностью до члена ряда, меньшего e=10-4, и значение функции (для проверки) f=ax, учесть, что 0,1£ x £1.

8. Вычислить значение суммы бесконечного ряда 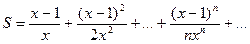с точностью до члена ряда, меньшего e=10-5, и значение функции (для проверки) f=lnx, учесть x>1.

9. Дано натуральное число N. Вычислить 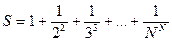. Функцию возведения в степень не использовать.

Вариант 3

1.

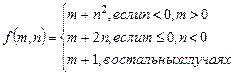
2.

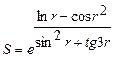
3. Даны два целых числа. Если они оба четны, то большее из них поделить на 2; если оба нечетны, то каждое умножить на 2; если числа разной четности, то нечетное увеличить на 1.

4. Составить программу поиска двузначных чисел таких, что если к сумме цифр этого числа прибавить квадрат этой суммы, то получится это число.

5. Пусть A и B – положительные вещественные числа, большие 1, причем A>B. Составить программу для поиска такого наименьшего натурального m, что Bm> m*A.

6. Дано натуральное число n. Составить программу для сравнения цифр старшего и младшего разрядов этого числа.

7. Вычислить значение суммы бесконечного ряда 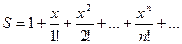с точностью до члена ряда, по модулю меньшего e=10-4, и значение функции (для проверки) f = ex , учесть, что 1£x£2.

8. Вычислить значение суммы бесконечного ряда с заданной точностью e=10-5 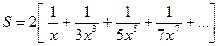и значение функции (для проверки) 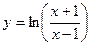, учесть, что |x|>1.

9. Для каждого из 10 значений переменной х, изменяющейся от –b до b с постоянным шагом, вычислить значение произведения Р=х*(х+0,2)*(х+0,4)*…*(х+1,8).

Вариант 4

1.

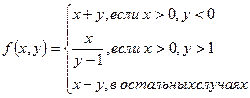
2.

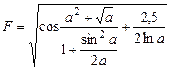
3. Даны 2 числа. Если они оба положительны, то поменять знак у большего из них; если оба отрицательны, то первое умножить на 2, а второе умножить на 3; если числа разных знаков, то меньшее заменить их полусуммой, а большее уменьшить на 1. Если хотя бы одно из чисел равно нулю, то изменять их не требуется.

4. Вывести на экран через запятую все делители натурального числа N.

5. Найти сумму целых положительных чисел, кратных четырем, из промежутка [А, В]. Значения А и В вводятся с клавиатуры.