{оператор_1; оператор_2; … оператор_ N ;}
Условный оператор, полная форма
if (выражение) оператор_1; else оператор_2;
Условный оператор, краткая форма
if (выражение) оператор;
Циклы с предусловием
while (выражение) оператор;
for (выражение_1; выражение_2; выражение_3) оператор;
Цикл с постусловием
do оператор; while (выражение);
Выражения, определяющие условия, могут быть любыми. Истинным считается значение, отличное от нуля.
Постановка задачи
Написать 9 программ согласно номеру индивидуального варианта.
В первой программе вычислить значение функции, используя условную операцию «?:».
Во второй программе вычислить значение по указанной формуле, используя функции математической библиотеки. Перед написанием программы требуется вычислить область определения функции (ООФ), в программе после ввода аргументов проверить их принадлежность ООФ.
В третьей программе использовать вложенный условный оператор.
В четвертой программе смоделировать арифметический цикл с помощью оператора цикла for.
В пятой и шестой программах использовать циклы while или do … while.
В седьмой и восьмой программах вычислить бесконечную сумму с заданной точностью, используя рекуррентные зависимости.
В девятой программе использовать конструкцию «цикл в цикле».
Варианты заданий
Вариант 1
1. 
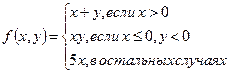
2. 
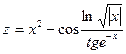
3. Вывести на экран номер четверти, которой принадлежит точка с координатами (x,y), или указать, какой оси принадлежит эта точка.
4. Ввести с клавиатуры натуральное число N>2. Вывести на экран последовательность вида «S=2*4*6*…*N», если N четное, или «S=1*3*5*…*N», если N нечетное.
5. Найти первое число Фибоначчи, большее заданного n (n>1). Каждый член последовательности Фибоначчи является суммой двух предыдущих
xn=xn-1+xn-2, x0=0, x1=1.
6. M и N – числитель и знаменатель обыкновенной дроби. Составить программу, позволяющую сократить эту дробь.
7. Вычислить значение суммы бесконечного ряда с точностью до члена ряда, по модулю меньшего e=10-4,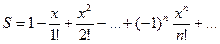 
, и значение функции (для проверки) f=e-x .
8. Вычислить значение суммы бесконечного ряда с заданной точностью e=10-6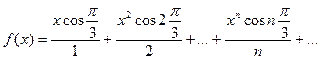 
, и значение функции (для проверки) 
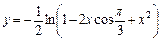учесть, что 
.
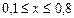9. Дано целое k>2. Напечатать все числа из диапазона [2,k], не являющиеся простыми. Простые числа не имеют других делителей, кроме 1 и самого себя.
Вариант 2
1. 
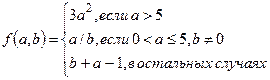
2. 
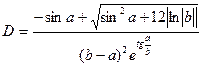
3. Даны два числа. Если они оба положительны, то большее из них заменить их средним арифметическим; если оба отрицательны, то поменять знак у меньшего из них; если числа имеют разные знаки, то каждое из них удвоить. Если хотя бы одно из чисел равно нулю, изменять их не требуется.