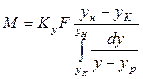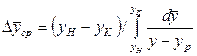6 Молекулярная диффузия. Закон Фика.
Молекулярной диффузией называется перенос распределяемого вещества, обусловленный беспорядочным тепловым движением молекул, атомов, ионов, коллоидных частиц. Молекулярная диффузия описывается первым законом Фика, согласно которому масса вещества dМ, продиффундировавшего за время dt через элементарную поверхность dF (нормальную к направлению диффузии), пропорциональна градиенту концентрации этого вещества:
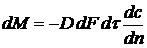 или
или 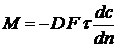 (1)
(1)
Из выражения (1) следует, что удельный поток вещества, переносимого молекулярной диффузией через единицу поверхности (F = 1) в единицу времени (t = 1), или скорость молекулярной диффузии, составляет
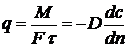 (2)
(2)
По своей структуре закон Фика аналогичен закону Фурье, описывающему передачу тепла теплопроводностью, причем аналогом градиента температур является в данном случае градиент концентраций, представляющий собой изменение концентрации диффундирующего вещества на единицу длины нормали между двумя поверхностями постоянных, но различных концентраций.
Коэффициент пропорциональности D в выражении закона Фика называется коэффициентом молекулярной диффузии, или просто коэффициентом диффузии. Знак минус перед правой частью первого закона Фика указывает на то, что молекулярная диффузия всегда протекает в направлении уменьшения концентрации распределяемого компонента. Согласно уравнению (1), коэффициент диффузии выражается как:
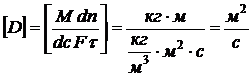
откуда (до сокращения одноименных величин) вытекает физический смысл D. Коэффициент диффузии, показывает, какая масса вещества диффундирует в единицу времени через единицу поверхности при градиенте концентрации, равном единице
Коэффициент молекулярной диффузии представляет собой физическую константу, характеризующую способность данного вещества проникать вследствие диффузии в неподвижную среду. Величина D таким образом не зависит от гидродинамических условий, в которых протекает процесс.
Турбулентная диффузия. Масса вещества dMт, переносимого в пределах фазы вследствие турбулентной диффузии, может быть принята, по аналогии с молекулярной диффузией, пропорциональной поверхности dF, времени dt и градиенту концентрации, и определяется по уравнению
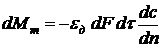 , (3)
, (3)
где 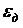 - коэффициент турбулентной диффузии. Коэффициент турбулентной диффузии
- коэффициент турбулентной диффузии. Коэффициент турбулентной диффузии  показывает какая масса вещества передается посредством турбулентной диффузии в единицу времени через единицу поверхности при градиенте концентрации, равном единице.
показывает какая масса вещества передается посредством турбулентной диффузии в единицу времени через единицу поверхности при градиенте концентрации, равном единице.
 7. Конвективная диффузия. Дифференциальное уравнение конвективной диффузии. Второй закон Фурье.
7. Конвективная диффузия. Дифференциальное уравнение конвективной диффузии. Второй закон Фурье.
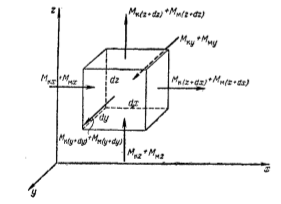
Суммарный перенос вещества вследствие конвективного переноса и молекулярной диффузии, по аналогии с теплообменом – конвективная диффузия. Распределение концентраций при переносе путем конвективной диффузии определяется диф уравнением. Выделив в потоке фазы элементарный параллелепипед с ребрами dx, dy, dz и рассматривая материальный баланс по распределяемому веществу можно прийти к соотношению 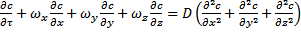
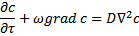 При массообмене в неподвижной среде, когда скорости потока равны нулю получаем второй закон Фика.
При массообмене в неподвижной среде, когда скорости потока равны нулю получаем второй закон Фика.
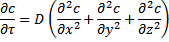
8. Второй закон Фика.
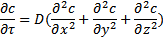
Уравнение носит название второго закона Фика. В дифференциальном уравнении конвективной диффузии, помимо конвекции, переменной является скорость потока. Поэтому данное уравнение надо рассматривать совместно с дифференциальными уравнениями гидродинамики: уравнениями Навье-Стокса и уравнением неразрывности потока.
 9. Механизм процесса массопереноса
9. Механизм процесса массопереноса
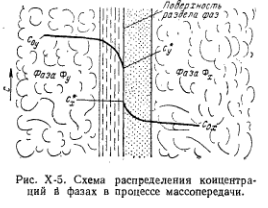
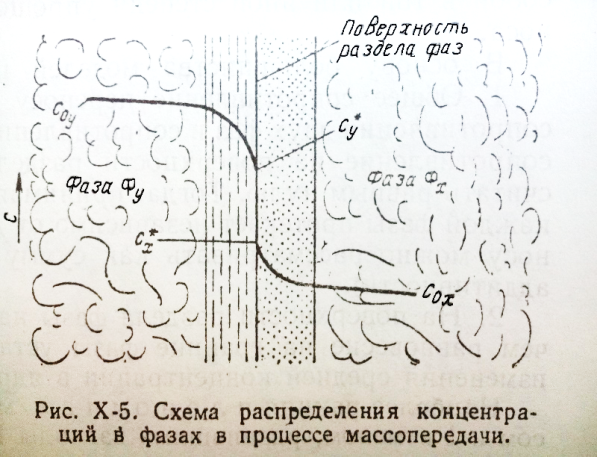
На рисунке Х-5 приведена схема, поясняющая процесс массопередачи между жидкостью и газом или между двумя жидкостями. Фазы движутся с некоторой скоростью друг относительно друга и разделены подвижной поверхностью раздела.
Перенос распределяемого вещества М (например, аммиака) происходит в условиях турбулентного движения фаз. Вещество переходит из вазы Фу, где концентрация вещества М выше равновесной (смеси аммиака с воздухом), в фазу Фх, например в воду. Осуществляется процесс массоотдачи из основной массы фазы Фу, к поверхности раздела фаз и процесс массоотдачи от поверхности раздела к основной массе фазы Фх. Таким образом происходит процесс массопередачи – переход вещества из одной фазы в другую.
В каждой фазе различают ядро, или основную массу фазы, и пограничный слой у границы фазы. В ядре вещество переносится турбулентными пульсациями и концентрация распределяемого вещества постоянна. В пограничном слое происходит постепенное затухание турбулентности, здесь наблюдается резкое изменение концентрации. У поверхности перенос сильно замедляется, т.к. скорость определяется скоростью молекулярной диффузии, здесь наблюдается наиболее резкое изменение концентрации.
Изменение концентрации объясняется тормозящим действием сил трения между фазами и сил поверхностного натяжения на границе жидкой фазы.
При турбулентном движении в ядре потока фазы перенос к границе раздела фаз осуществляется параллельно молекулярной и турбулентной диффузии. В пограничном слое скорость переноса лимитируется скоростью молекулярной диффузии. Для интенсификации массопереноса нужно уменьшить толщину пограничного слоя, повышая степень турбулентности потока, путем увеличения до некоторого предела скорости фазы.
10. Уравнение массоотдачи
Принимают, что скорость массоотдачи пропорциональна движущей силе, равной разности концентраций в ядре и на границе фазы (в случае обратного направления переноса) – разности концентраций на границе и в ядре фазы. В связи со сложностью механизма массоотдачи в практических расчетах используют относительно простое уравнение:
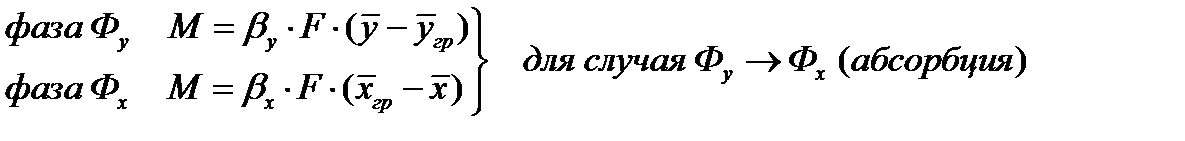
где у и х – средние концентрации в ядре каждой фазы;
угр и хгр – концентрации у границы соответствующей фазы;
bу и bх – коэффициенты пропорциональности, которые называют коэффициентами массоотдачи;
F – поверхность контакта фаз, м2.
11. Зависимость между коэффициентами массоотдачи и массопередачи.
Чтобы установить зависимость между β и К, обычно принимают, что на границе раздела фаз достигается равновесие, т.е. сопротивлением переносу через границу раздела фаз можно пренебречь. Отсюда вытекает положение аддитивности фазовых сопротивлений, которое является одной из предпосылок для расчета к-та массопередачи. Допустим, что распределяемое вещество переходит из фазы Фу в Фх,и движущая сила массопередачи выражается в концентрациях фазы. Фу. М= Ку F ( y - y * ) (1)– количество массопередачи вещества, переходящее из фазы в фазу при установившемся процессе.
Равновесная зависимость между концентрациями в фазах линейна, т.е. линия равновесия описывается ур-нием у*= mx, где m – тангенс угла наклона линии равновесия. Выразим движущую силу в уравнении массоотдачи (M=βyF ( 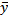 -
- 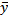 гр ), M=βхF (
гр ), M=βхF ( 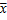 -
- 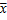 гр )) в конц-циях фазы Фу, принимая, что концентрации распределяемого вещества, в фазах непосредственно у границы (хгр, угр) равновесны друг другу. Тогда из уравнения линии равновесия следует, что хгр = угр/ m и х = у*/ m , где у* - концентрация фазы Фу, равновесная с концентрацией х фазы Фх. Подставляя эти значения хгр и х в уравнение массоотдачи, получим:
гр )) в конц-циях фазы Фу, принимая, что концентрации распределяемого вещества, в фазах непосредственно у границы (хгр, угр) равновесны друг другу. Тогда из уравнения линии равновесия следует, что хгр = угр/ m и х = у*/ m , где у* - концентрация фазы Фу, равновесная с концентрацией х фазы Фх. Подставляя эти значения хгр и х в уравнение массоотдачи, получим:
М= βу F 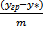 ,
,
откуда 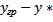 =
= 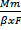 ; y - y * =
; y - y * = 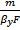 , складывая эти два уравнения, исключаем концентрацию:
, складывая эти два уравнения, исключаем концентрацию:
y - y * = 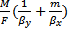 , из уравнения массопередачи(1) находим
, из уравнения массопередачи(1) находим
y - y * = 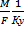 , сокращая получим
, сокращая получим
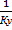 =
= 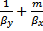
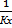 =
= 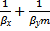
Левые части уравнений представляют собой общее сопротивление переносу вещества из фазы в фазу, т.е. сопротивление массопередаче, правые – сумму сопротивлений массоотдаче в фазах. Поэтому эти зависимости являются уравнениями аддитивности фазовых сопротивлений.
12. Подобие процессов переноса массы. Диффузионные критерии подобия.
Наиболее строгий и принципиально возможный путь для определения коэффициентов массоотдачи заключается в интегрировании уравнения диффузии в движущейся среде совместно с уравнениями Навье-Стокса и уравнением неразрывности потока при заданных начальных и граничных условиях. Рассмотрим подобие граничных условий на границе между ядром потока фазы и пограничным слое, а также на границе раздела фаз. На границе ядра потока с пограничным слоем с0=сonst. Подобие переноса вещества у границы раздела фаз установим на основе представления о диффузионном пограничном подслое. Масса вещества, переносимая в единицу времени к границе фазы в соответствии с уравнением массоотдачи составляет:М=ẞуF(y-yгр).Так же масса вещества переносится молекулярной диффузией через пограничный слой и равна: М=-DF 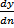 .Подобие условий переноса на границе фазы : ẞy(y-yгр)=-D
.Подобие условий переноса на границе фазы : ẞy(y-yгр)=-D 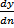 .Обозначив y-yгр через ∆у, запишем это уравнение в виде ẞy∆у=-D
.Обозначив y-yгр через ∆у, запишем это уравнение в виде ẞy∆у=-D 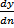 .Так как для подобных процессов отношение сходственных величин равно отношению величин им пропорциональных,заменим dy конечной разностью ∆у, и dn – некоторым линейным размером l. Получаем
.Так как для подобных процессов отношение сходственных величин равно отношению величин им пропорциональных,заменим dy конечной разностью ∆у, и dn – некоторым линейным размером l. Получаем 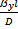 =idem. Данный комплекс является безразмерным и в соответствии с первой теоремой подобия представляет собой критерий подобия. Этот комплекс носит название диффузионного критерия Нуссельта Nu/=
=idem. Данный комплекс является безразмерным и в соответствии с первой теоремой подобия представляет собой критерий подобия. Этот комплекс носит название диффузионного критерия Нуссельта Nu/= 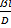 .Диффузионный критерий Фурье Fo/=
.Диффузионный критерий Фурье Fo/= 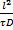 . Диффузионный критерий Пекле Pe/=
. Диффузионный критерий Пекле Pe/= 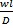 . Критерий Пекле выражает меру отношения массы вещества, перемещаемой путём конвективного переноса и молекулярной диффузии, в сходственных точках подобных систем. Подобие распределения концентраций и одновременно подобие скоростей в потоках соблюдается в общем случае при следующих условиях Fo/=
. Критерий Пекле выражает меру отношения массы вещества, перемещаемой путём конвективного переноса и молекулярной диффузии, в сходственных точках подобных систем. Подобие распределения концентраций и одновременно подобие скоростей в потоках соблюдается в общем случае при следующих условиях Fo/= 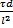 =idem Pe/=
=idem Pe/= 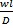 = idem Re=
= idem Re= 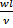 = idem .Диффузионный критерий подобия Прандтля Pr/=
= idem .Диффузионный критерий подобия Прандтля Pr/= 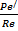 =
= 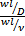 =
= 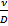 =
= 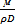 .Общая функциональная зависимость Nu/ от определяющих критериев и симплексов подобия для неустановившихся процессов массоотдачи может быть выражена как Nu/=f(Fo/, Pe/, Re,Fr,Г1,Г2…)либо иной комбинацией определяющих критериев подобия.
.Общая функциональная зависимость Nu/ от определяющих критериев и симплексов подобия для неустановившихся процессов массоотдачи может быть выражена как Nu/=f(Fo/, Pe/, Re,Fr,Г1,Г2…)либо иной комбинацией определяющих критериев подобия.
13. Средняя движущая сила массопередачи
Рассмотрим определение средней движущей силы, когда линия равновесия определяется уравнением кривой (рис) 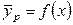 в противоточном массообменном аппарате при условии
в противоточном массообменном аппарате при условии 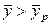 .
.
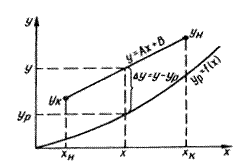
Примем, что расходы фаз G и L постоянны, коэффициенты массопередачи 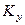 и
и 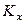 не меняются по длине аппарата,
не меняются по длине аппарата, 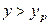 и перенос вещества происходит из фазы G в фазу L.
и перенос вещества происходит из фазы G в фазу L.
Для элемента поверхности на основании уравнения материального баланса можно записать 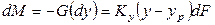 .
.
Разделяя переменные 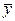 и F и интегрируя это выражение в пределах изменения концентрации от yн до yк и поверхности контакта фаз от 0 до F, получим
и F и интегрируя это выражение в пределах изменения концентрации от yн до yк и поверхности контакта фаз от 0 до F, получим
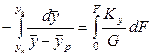
откуда
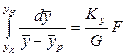
Согласно уравнению материального баланса количество вещества, перешедшего из фазы G в фазу L, равно 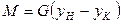 . Подставим G из последнего выражения в уравнение
. Подставим G из последнего выражения в уравнение
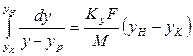
откуда