На рис. 7.3, а, б показаны схема и ЛЧХ звена с отставанием по фазе, которое используется в системах РА как последовательное корректирующее устройство. Его передаточная функция имеет вид

Дата: 2025-05-25; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

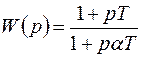, (7.28)

где Т=R₂С – постоянная времени звена; 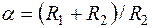– постоянный коэффициент.

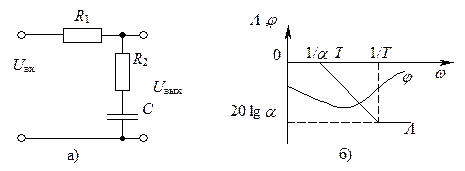
Рис. 7.3 - Схема (а) и ЛЧХ (б) корректирующего звена

с отставанием по фазе

На рис. 7.4, а, б представлены схема и ЛЧХ последовательного корректирующего звена с опережением по фазе, передаточная функция которого

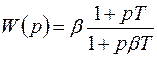, (7.29)

где Т=R₁С; 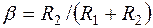– постоянный коэффициент.

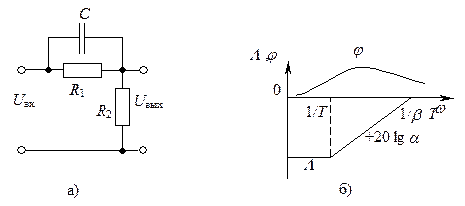
Рис. 7.4 - Схема (а) и ЛЧХ (б) корректирующего звена

с опережением по фазе

В системах РА применяют также последовательное комбинированное звено, схема которого и ЛЧХ изображены на рис. 7.5, а, б. Передаточная функция звена имеет вид

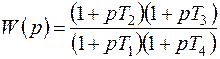. (7.30)

Сопротивления и емкости выбираются такими, чтобы выполнялось условие Т₁>Т₂>Т₃>Т₄. С этой целью необходимо, чтобы C₂>C₁ и R₁>R₂. Тогда сопротивления и емкости звена рассчитывают по известным постоянным времени

; ; ;

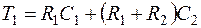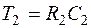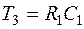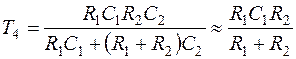. (7.31)

В качестве корректирующих обратных связей используют жесткие и гибкие связи.

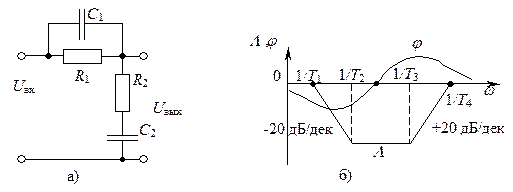
Рис. 7.5 - Схема (а) и ЛЧХ (б) комбинированного корректирующего

звена

Жесткая обратная связь не содержит дифференцирующих звеньев. Рассмотрим ее влияние на характеристики отдельных звеньев. Если жесткой обратной связью охватить инерционное звено, то, согласно (4.5),

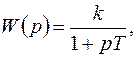
где k = k₁/(1+k₁k₀); T = T₁/(l+k₁k₀); k₁, T₁ – коэффициент передачи и постоянная времени инерционного звена, охваченного обратной связью; k_o – коэффициент передачи обратной связи.

Таким образом, при охвате инерционного звена жесткой обратной связью не изменяется его тип, однако коэффициент усиления и постоянная времени уменьшаются в (l+k₁k₀) раз.

Если жесткой обратной связью с коэффициентом передачи k₀ охватить интегрирующее звено с коэффициентом передачи k₁, то получим инерционное звено с параметрами k = 1/k₀, T = 1/(k₁k₀) (изменяется тип звена). Следовательно, такую связь необходимо использовать в тех случаях, когда требуется понизить порядок астатизма, т.е. исключить в системе влияние интегрирующего звена.

Гибкая обратная связь содержит дифференцирующие звенья, поэтому она действует только в переходном процессе, что не снижает точности системы в установившемся режиме. Оценим влияние гибкой обратной связи на характеристики различных звеньев. Если такой связью с передаточной функцией

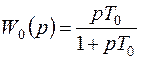(7.32)

охватить безынерционное звено, то получим звено с передаточной функцией

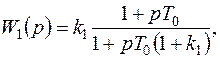(7.33)

где k₁ – коэффициент передачи безынерционного звена.

Таким образом, охват безынерционного звена гибкой обратной связью эквивалентен включению в цепь сигнала ошибки системы последовательного звена с отставанием по фазе.

Если гибкой обратной связью с передаточной функцией (7.32) охватить интегрирующее звено, то

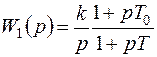, (7.34)

где 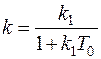; ; 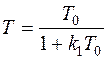k₁ – коэффициент передачи интегрирующего звена.

Из выражения (7.34) следует, что охват интегрирующего звена гибкой обратной связью эквивалентен последовательному включению в цепь сигнала ошибки системы звена с опережением по фазе, при этом астатизм системы РА не снижается.

Для создания такого вида связи используются тахогенераторы, гироскопические датчики частоты вращения, RC-цепи. На рис. 7.6, а показана схема RС-цепи, передаточная функция которой определяется (7.32). Сигнал на выходе такой цепи в определенном диапазоне частот пропорционален первой производной u_вых(t).

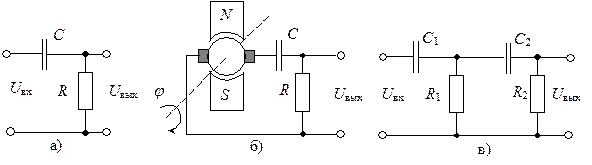
Рис. 7.6 - Гибкие обратные связи

В системах РА применяются гибкие обратные связи, выходной сигнал которых пропорционален второй производной входного сигнала обратной связи. Такая обратная связь (рис. 7.6, б) может быть сформирована с помощью тахогенератора и дифференцирующей RC-цепи, если входным сигналом обратной связи является угол поворота, или с помощью RС-цепи, изображенной на рис. 7.6, в, если на входе подается сигнал постоянного тока. Передаточная функция такой цепи

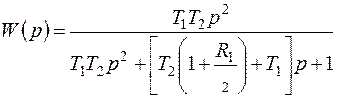, (7.35)

где ; .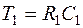

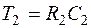Если R₁<<R₂, то приближенно можно принять, что

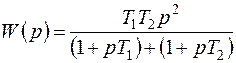. (7.36)

Пример. Синтезировать систему автоматического сопровождения цели РЛС (рис. 7.7). Найти передаточные функции корректирующих устройств из условия обеспечения в системе полосы пропускания, равной 10 с^–1. Показатель колебательности не превышает 1,4, ошибка по положению равна нулю, ошибка по скорости – не более 0,175×10^–2 рад и ошибка по ускорению – не более 0,87×10^–2 рад при максимальных значениях производных сигнала 0,175 рад×с^–1 и 0,35 рад×с^–2.

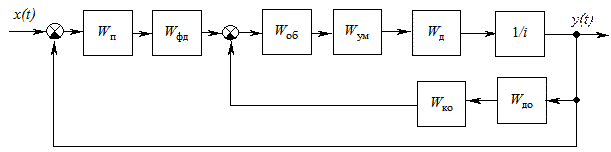
Рис. 7.7 - Структурная схема системы автосопровождения

цели РЛС

Решение. Передаточная функция исходной части системы

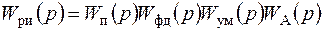, (7.37)

где 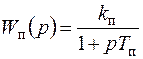; ; 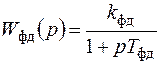; 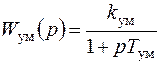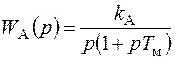- передаточные функции приемника, фазового детектора, усилителя мощности и антенны с двигателем и редуктором.

Параметры устройств исходной части системы: k_п = 0,035 В/рад; k_фд=0,8; k_ум = 10; k = 143 рад/(с В); T_п = T_фд = T_п=0,01 с; T_м = =0.02 с.

Коэффициент передачи исходной части системы

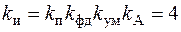. (7.38)

С учетом требований к системе и формул (7.9)–(7.12)

D j = 0,785 рад; w_ср = 7 с^–1; С₀ = 0; С₁ = 0,01 с; С₂ = 0,05 с²; К =100 с^–1.

В качестве желаемой передаточной функции разомкнутой системы примем функцию (7.7). Все частоты сопряжения передаточных функций устройств исходной части системы автоматического сопровождения (7.37) больше требуемой частоты среза, поэтому для упрощения корректирующих устройств включим передаточную функцию исходной части системы в состав желаемой передаточной функции. В результате получим

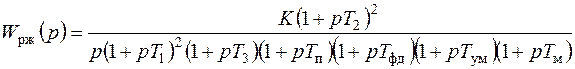.(7.39)

Постоянные времени T₁, T₂ и Т₃ вычислим по формулам (7.19) и (7.20). Тогда T₁ = 1,7 с; T₂ = 0,45 с; T₃ = 0,015 с.

Так как значение T₃ незначительно отличается от постоянной времени двигателя T_м=0,02 с, то для упрощения корректирующего устройства примем Т₃=Т_м.

Передаточную функцию последовательного корректирующего устройства найдем, используя выражение (7.22):

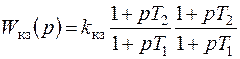, (7.40)

где k_кз = К/К_и–коэффициент передачи корректирующего звена;

К_и – коэффициент передачи исходной части системы.

Первый сомножитель в (7.40) реализуем в виде последовательного корректирующего устройства, включенного после фазового детектора, а второй – через эквивалентную обратную связь, передаточную функцию которой рассчитаем по формуле (7.24). Таким образом,

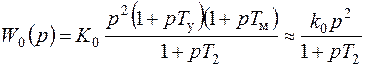, (7.41)

где k₀ = (T₁–T₂)/(k_yk_A) – коэффициент передачи цепи обратной связи.

В выражении (7.41) пренебрегли постоянными времени T_у и Т_м, так как соответствующие им частоты сопряжения намного больше частоты среза. Обратная связь с передаточной функцией (7.41) реализуется с помощью тахогенератора и дифференцирующей RC-цепи (рис. 7.6, б) с постоянной времени, равной T₂. Передаточная функция цепи такой обратной связи имеет вид

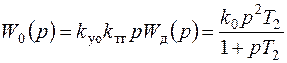, (7.42)

где k_тг – коэффициент передачи тахогенератора; k_уо = k₀/(k T₂) – коэффициент усиления усилителя в цепи обратной связи.

Так как при синтезе системы автоматического сопровождения были допущены упрощения, то необходимо проверить выполнение заданных требований. С этой целью на рис. 7.8 построены ЛЧХ спроектированной системы и ЛЧХ, соответствующие передаточной функции (7.39).

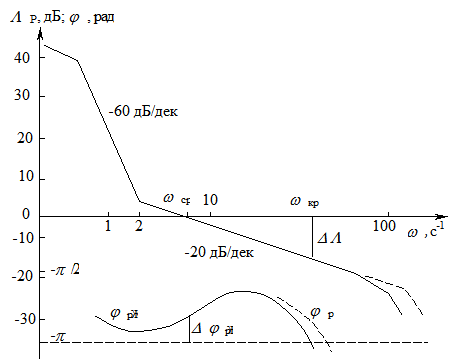
Рис. 7.8 - ЛЧХ системы автосопровождения цели РЛС

Из сравнений этих характеристик видно, что выполняются все заданные показатели качества работы системы автоматического сопровождения цели.

7.4 Синтез систем с неполной информацией о воздействиях

Ранее, при динамическом синтезе систем РА полагали, что характеристики управляющих воздействий и помех известны, т.е. заданы их математические ожидания и спектральные плотности случайных составляющих.

На практике это не всегда так. Характеристики воздействий обычно известны не полностью. Кроме того, они изменяются в процессе работы системы, поэтому показатели качества работы могут оказаться ниже расчетных.

Построение систем РА с использованием адаптивных систем позволяет исключить зависимость показателей качества работы от изменения характеристик воздействия и нестабильности параметров устройств. На практике используют так называемые робастные системы (от английского слова robust – грубый). Техническая реализация таких систем РА, по сравнению с адаптивными системами, намного проще, что является их существенным преимуществом.

Синтез робастных систем может быть выполнен различными методами. Применительно к задачам синтеза систем РА целесообразно использовать метод, основанный на известных средних квадратических значениях управляющего воздействия и его производных. Данный метод не связан с конкретной формой спектральной плотности управляющего сигнала, поэтому ее изменение не приводит к несоблюдению точности работы системы РА.

Рассматриваемый метод синтеза систем РА сводится к выбору частотной характеристики ошибки из условия непревышения средней квадратической ошибкой заданного значения. После этого можно сформулировать требования к частотной характеристике разомкнутой системы.

Дисперсия ошибки относительно управляющего воздействия в соответствии с выражением (6.22) определяется как

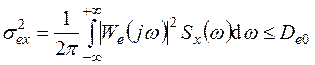, (7.43)

где W_е(j w) – частотная характеристика ошибки; D_e0 – допустимое значение дисперсии ошибки.

Представим квадрат АЧХ ошибки в следующем виде:

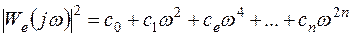. (7.44)

Тогда дисперсия ошибки (7.43)

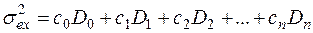, (7.45)

где D₀ – дисперсия управляющего воздействия; D₁ – дисперсии производных; с_i – постоянные коэффициенты.

Задача синтеза системы состоит в выборе характеристики W_е(j w), удовлетворяющей условию (7.43). Если известна только дисперсия управляющего воздействия D₀, то из выражения (7.45) следует, что с₀ = D_e0/D₀ и частотная характеристика ошибки проектируемой системы должна удовлетворять условию

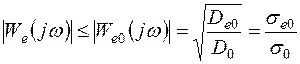, (7.46)

где |W_е0(j w)| – АЧХ ошибки, составленная по априорным сведениям об управляющем воздействии.

Таким образом, ошибка не должна превышать значения (7.46) в диапазоне частот, в котором возможны спектральные составляющие управляющего воздействия.

В том случае, если известна только дисперсия первой производной управляющего воздействия D₁, то с₁ = =D_е0/D₁ и частотная характеристика ошибки проектируемой системы должна удовлетворять условию

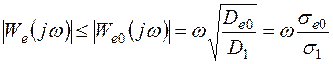. (7.47)

Если известна только дисперсия второй производной управляющего воздействия, то

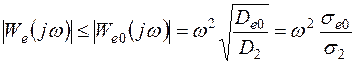. (7.48)

От ограничений, накладываемых на АЧХ ошибки, можно перейти к требованиям, которым должна удовлетворять частотная характеристика разомкнутой проектируемой системы. Из выражений (4.30) и (4.34) следует, что

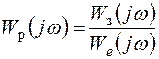. (7.49)

Так как на частотах меньше частоты среза |W_з(j w)| » 1, то условия (7.46) – (7.48) выполняются, если

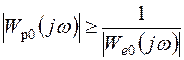, (7.50)

а ФЧХ разомкнутой системы может быть произвольной.

На частотах больше частоты среза |W_з(j w)| » |W_р(j w)| и поэтому вид частотной характеристики разомкнутой системы не влияет на точность системы РА и может быть произвольным, но при этом требования к запасам устойчивости должны соблюдаться.

Выполнение условия (7.50) гарантирует, что динамическая ошибка будет не выше заданной.

Очевидно, что выражениям (7.46) и (7.50) (рис. 7.9) соответствует прямая линия, параллельная оси частот и отстоящая от нее на 20 lg s₀/ s _e0, условиям (7.47) и (7.50) – прямая с наклоном – 20 дБ/дек, которая пересекает ось абсцисс на частоте, равной s₁/ s _e0, а условиям (7.48) и (7.50) – прямая с наклоном – 40 дБ/дек, которая начинается на оси абсцисс с частоты 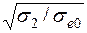. Эти прямые образуют запретную область, в которой не должна располагаться низкочастотная часть логарифмической АЧХ разомкнутой проектируемой системы РА. Частоты, соответствующие точкам излома запретной области, вычисляют по формулам

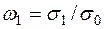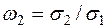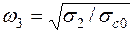; ; . (7.51)

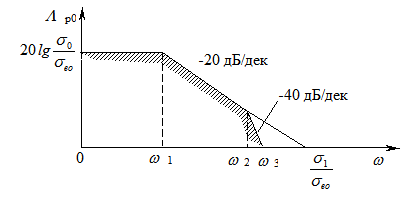
Рис. 7.9 - ЛЧХ запретной области относительно динамической ошибки

Рассмотрим ограничения на вид АЧХ разомкнутой проектируемой системы из-за действия помехи, спектральная плотность которой известна и постоянна в пределах полосы пропускания системы РА (помеха в виде белого шума). Тогда дисперсия ошибки из-за действия помехи определяется в виде

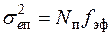, (7.52)

где f_эф – эффективная полоса пропускания системы;

N_п – уровень спектральной плотности белого шума помехи.

Задача синтеза системы РА заключается в том, чтобы суммарная средняя квадратическая ошибка системы не превышала допустимого значения:

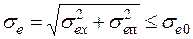, (7.53)

где s_еп – средняя квадратическая ошибка из-за действия помехи.

Условие (7.53) накладывает противоречивые требования к проектируемой системе РА. С одной стороны, средняя квадратическая ошибка относительно сигнала должна быть меньше s_е0, так как в противном случае не будет выполнено условие (7.53), а с другой – не должна превышать этого значения и составляющая ошибки s_еп. Поэтому эффективная полоса пропускания проектируемой системы определяется неравенством

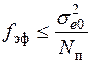. (7.54)

Таким образом, при синтезе системы РА необходимо обеспечить одновременное удовлетворение условий (7.50) и (7.54). Если эти условия выполнить одновременно невозможно, то при заданном значении s_е0 решения задачи проектирования робастной системы РА не существует.

Определим, какие ограничения накладывает условие (7.54) на АЧХ разомкнутой системы. С этой целью рассмотрим типовую логарифмическую АЧХ, низкочастотные участки которой содержат асимптоты с наклонами –20, –40 или –60 дБ/дек. При этом, всегда в области частоты среза наклон логарифмической АЧХ равен –20 дБ/дек, так как только в этом случае можно обеспечить необходимый запас устойчивости по фазе.

В [8] показано, что для систем РА с такими наклонами логарифмической АЧХ разомкнутой системы эффективная полоса пропускания системы с достаточной для практики точностью определяется по формуле

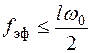, (7.55)

где w₀ – частота, соответствующая точке пресечения асимптоты логарифмической АЧХ с наклоном –20 дБ/дек с осью абсцисс; l – коэффициент, равный 1, 2 или 3, в зависимости от наклона асимптоты, для которой определена частота w₀. Согласно (7.54) и (7.55),

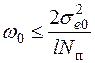. (7.56)

Это выражение определяет крайнее допустимое положение логарифмической АЧХ разомкнутой проектируемой системы РА, т.е. границу запретной области, в которой не должна располагаться логарифмическая АЧХ разомкнутой системы. Построение запретной области осуществляется следующим образом. На оси абсцисс (рис. 7.10) через точку 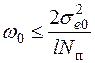проводят прямую с наклоном –20 дБ/дек, а через точки w_о/2 и w_о/3 прямые с наклонами –40 и –60 дБ/дек. В результате формируется запретная область, заштрихованная на рис. 7.10, а.

Требования к точности работы проектируемой системы РА относительно возмущающего воздействия выполняются, если ее логарифмическая АЧХ не заходит в запретную область.

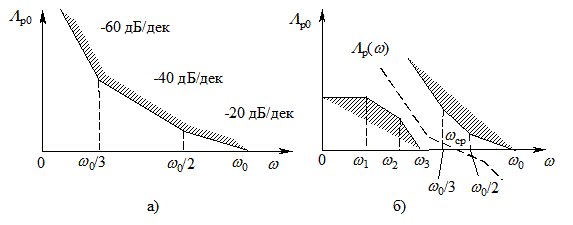
Рис. 7.10 - ЛЧХ запретной области относительно возмущающего

воздействия (а) и ЛЧХ общей запретной области (б)

На рис. 7.10, б показаны две запретные области, определенные ранее. Для обеспечения в проектируемой системе РА заданной точности необходимо, чтобы выбранная логарифмическая АЧХ разомкнутой системы не располагалась в запретных областях и удовлетворяла требованиям к запасам устойчивости. На рис. 7.10, б такая характеристика показана пунктиром. Если запретные области на рис. 7.10, б перекрываются, то синтез робастной системы при заданных точностных характеристиках невозможен. Для гарантированного получения заданной точности должен быть обеспечен некоторый интервал между левой и правой запретными областями. Минимальная ширина этого интервала должна составлять около четверти декады.

7.5 Комплексные системы

Системы РА, которые формируются не только на базе радиотехнических устройств, но и на базе устройств других типов (например, гироскопических приборов, инерциальных систем и др.), называют комплексными. Подобные системы широко применяются при навигации для определения координат и параметров движения различных объектов (например, для измерения скорости летательного аппарата и угла сноса относительно расчетной траектории используется гироскопическая система с доплеровским измерителем). Для измерения высоты полета применяются барометрический и радиолокационный высотомеры. Для комплексной системы РА характерно наличие нескольких параллельно работающих каналов с различными датчиками измерения одной и той же информации. На рис. 7.11 показана типовая структурная схема комплексной измерительной системы, в которой входной сигнал 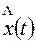измеряется разнотипными датчиками Д₁, Д₂, ..., Д_n с передаточными функциями W_дi(p), где i=l, 2, ..., n; воздействия V_i(t) учитывают погрешности датчиков. Комплексирование системы заключается в вычислении оценки x(t) с точностью, превышающей достижимую при раздельном использовании датчиков. Из схемы (рис. 7.11) следует, что преобразование Лапласа для оценки входного сигнала будет иметь вид

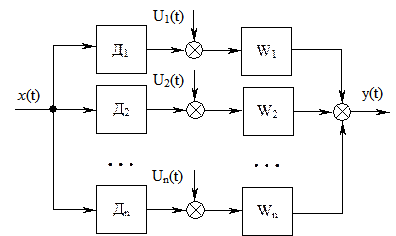
Рис. 7.11 - Типовая структурная схема комплексной измерительной

системы РА

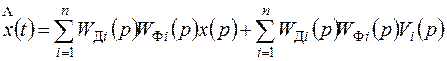. (7.57)

Преобразование Лапласа для сигнала ошибки имеет вид

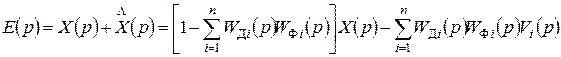. (7.58)

Из последнего выражения следует, что если передаточные функции каналов системы выбирают из условия

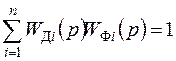, (7.59)

то выражения (7.57) и (7.58) принимают вид

;

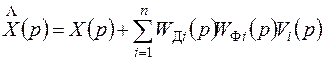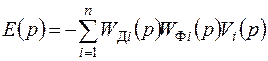. (7.60)

Таким образом, ошибка комплексной системы не зависит от характеристик измеряемого сигнала и определяется только погрешностями датчиков.