7 ОСНОВЫ Проектирования систем радиоавтоматики

Дата: 2025-05-25; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

7.1 Постановка задачи

Задача проектирования системы РА состоит в выборе структурной схемы параметров и способа технической реализации системы из условия обеспечения требований, которые следуют из назначения проектируемой системы и обеспечения заданных характеристик. Один из возможных способов описания требований к проектируемой системе – задание показателей качества работы системы, таких как статическая, динамическая и среднеквадратическая ошибки системы. Это справедливо, когда известны характеристики системы управляющих и возмущающих воздействий. Детерминированные воздействия должны быть заданы как функции времени или их производные. Для случайных сигналов и помех должны быть известны их корреляционные функции или спектральные плотности. При такой постановке синтез системы сводится к выбору структурной схемы, с помощью которой можно обеспечить заданные показатели качества работы системы РА.

Если характеристики управляющих и возмущающих воздействий известны, то систему РА можно спроектировать как оптимальную, обеспечив минимальное значение суммарной среднеквадратической ошибки. Решить эту задачу позволяет теория оптимальных фильтров Н. Винера и Р. Калмана, которая применима к проектированию оптимальных систем РА. Возможна и иная постановка задачи синтеза оптимальных систем. Наиболее общей является ее постановка с учетом достижения минимума функционала (критерия качества)

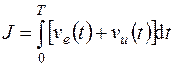, (7.1)

где 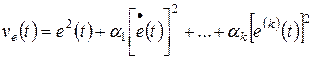– квадратичная форма относительно ошибки системы 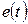; 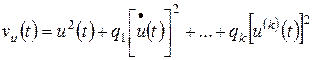– квадратичная форма относительно сигнала управления 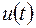; T – время работы системы.

Первая квадратичная форма в функционале (7.1) выбирается из требований, предъявляемых к точности проектируемой системы, вторая учитывает ограничения на сигнал управления. При этом задача оптимального синтеза формулируется следующим образом. Из допустимого множества u(t) необходимо выбрать и технически реализовать такой сигнал управления, который переводит объект управления из начального состояния в конечное и минимизирует функционал (7.1). Для решения таких задач используются методы вариационного исчисления, принцип максимума Л.С. Понтрягина, метод динамического программирования Р. Белмана. Здесь возможны два случая: 1) полностью известна информация о состоянии объекта управления; 2) информация об объекте управления неполная или вообще неизвестна. Во втором случае при синтезе системы возникает дополнительная задача оценки состояния объекта управления, на основании которой формируется оптимальный сигнал управления.

Синтез оптимальных систем из условия минимума функционала (7.1) связан с рядом трудностей. Одна из трудностей состоит в том, что в настоящее время нет каких-либо методов, позволяющих связать коэффициенты квадратичных форм функционала (7.1) a _i и q_i, с заданными показателями качества работы проектируемой системы. Поэтому в процессе синтеза системы приходится рассчитывать большое число вариантов оптимальных систем с различными видами квадратичных форм и их коэффициентов, объем расчетов при этом может быть весьма значительным. Другая трудность связана с реализацией найденных оптимальных алгоритмов управления, которые получаются особо сложными и могут быть реализованы лишь приближенно. Вследствие отмеченных трудностей методы проектирования оптимальных систем из условия минимума функционала (7.1) в основном используются в научных исследованиях для оценки предельных соотношений и мало пригодны в инженерных задачах проектирования систем РА.

В данной главе рассматривается синтез систем РА из условия обеспечения допустимых ошибок в системе и удовлетворения других показателей качества работы. Такой метод называют динамическим синтезом систем РА.

Помимо требований к качеству функционирования в процессе синтеза систем РА предъявляются требования и к их сложности. Всегда желательно, чтобы спроектированная система была простой, а требования к элементам системы – минимальными. В качестве функционала сложности системы можно применять следующий интеграл [8]:

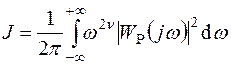, (7.2)

где W_p(j w) –частотная характеристика разомкнутой системы; v – порядок астатизма.

Чем меньше значение интеграла (7.2), тем ниже требования к устройствам системы. Помимо требований к качеству работы проектируемой системы РА, к ее сложности предъявляется и ряд требований, связанных с надежностью работы системы, стабильностью ее характеристик при изменении условий окружающей среды, эксплуатацией, массой, габаритами и т.п. В настоящее время теория оптимальных систем не позволяет объединить всю совокупность требований к проектируемой системе в виде единого критерия, поэтому удовлетворение их во многом зависит от опыта и квалификации инженера-исследователя.

7.2 Синтез передаточной функции разомкнутой системы радиоавтоматики

Синтез систем РА имеет своей целью выбор ее структуры и параметров так, чтобы удовлетворялись определенные (заданные) требования к качеству регулирования. При этом известен объект регулирования, т.е. имеются его характеристики (математическое описание), а иногда уже выбраны основные функциональные элементы регулятора.

Синтез объекта регулирования есть лишь один из этапов ее проектирования. Синтезу предшествует, по крайне мере, следующее:

1. Исследование объекта регулирования для определения его динамических свойств и условий, в которых его используют. Динамические свойства определяют теоретически или на основе экспериментальных исследований и фиксируют в виде дифференциального уравнения (системы уравнений) или передаточной функции.

2. Составление требований к качеству регулирования. Требования определяются назначением объекта, а также опытом проектирования и эксплуатации системы подобного класса.

3. Выбор основных элементов регулятора (датчика регулируемой величины, элемента сравнения, усилителя и исполнительного элемента) и определение их динамических свойств.

При синтезе систем РА полагают, что по известным характеристикам управляющих и возмущающих воздействий определены допустимые значения ошибок по положению, скорости, ускорению, ширине полосы пропускания, найденной из условия обеспечения требуемого значения средней квадратической ошибки, а также допустимая колебательность системы. Требования к указанным ошибкам формулируются в виде следующих неравенств:

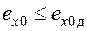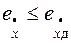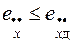; ; , (7.3)

где 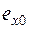; ; 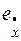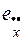– ошибки проектируемой системы по положению, скорости и ускорению.

На первом этапе задача синтеза систем РА состоит в нахождении желаемой передаточной функции разомкнутой системы, которая позволяет удовлетворить заданные требования к проектируемой системе РА. Очевидно, что желаемую передаточную функцию разомкнутой системы следует формировать в более простом виде. Желаемая передаточная функция разомкнутой системы имеет вид

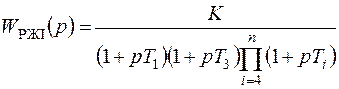; (7.4)

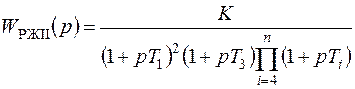. (7.5)

При синтезе систем с астатизмом первого порядка передаточная функция определяется по выражению

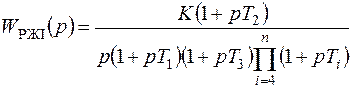; (7.6)

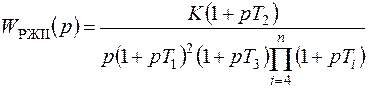. (7.7)

При проектировании систем с астатизмом второго порядка желаемая передаточная функция разомкнутой системы имеет вид

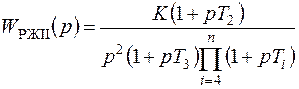, (7.8)

где П – знак произведения.

Задача синтеза систем РА сводится к определению по заданным показателям качества параметров желаемой передаточной функции К, Т₁, Т₂ и T₃. Звенья с постоянными времени T_i в такой функции учитывают влияние на проектируемую систему РА устройств с малыми постоянными времени (например, приемника РЛС в системе автоматического сопровождения цели и т.п.).

Прежде, чем рассматривать методику нахождения параметров желаемой передаточной функции, проанализируем типичные логарифмические АЧХ, соответствующие передаточным функциям (7.6) и (7.7) (рис. 7.1). На этих характеристиках различают три диапазона частот. Вид характеристики в диапазоне низких частот (ДНЧ) характеризует точность работы системы относительно управляющего воздействия. В диапазоне средних частот (ДСЧ) находится частота среза. В этом диапазоне частот вид характеристики определяет запас устойчивости по фазе, полосу пропускания, показатели качества переходного процесса. Вид характеристики в диапазоне высоких частот (ДВЧ) влияет на запасы устойчивости в системе РА.

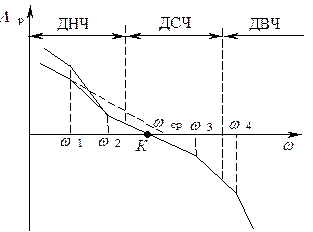
Рис. 7.1 - ЛЧХ разомкнутых систем РА

Найдем параметры желаемой передаточной функции системы с астатизмом первого порядка (7.6). По заданному значению колебательности системы и формуле (6.7) вычисляют запас устойчивости по фазе:

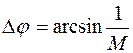. (7.9)

Требуемое значение полосы пропускания и выражение (6.6) позволяют рассчитать частоту среза проектируемой системы:

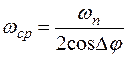. (7.10)

По допустимым значениям ошибок по скорости и ускорению находят коэффициенты ошибок:

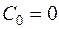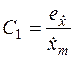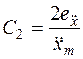, , , (7.11)

где 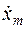, 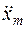– максимальные значения первой и второй производных от управляющего воздействия.

Коэффициент ошибки по скорости определяет коэффициент усиления в системе РА:

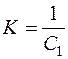. (7.12)

Для нахождения постоянных времени Т₁ и Т₂, установим связь частот сопряжения w₁ = l/T₁ и w₂ = l/T₂ с коэффициентом усиления и частотой среза. Из рис. 7.1 следует, что

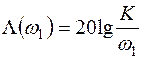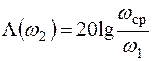, . (7.13)

Наклон характеристики между частотами w₁ и w₂ равен – 40 дБ/дек, поэтому

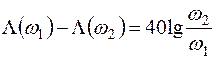. (7.14)

Согласно (7.13) и (7.14),

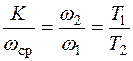. (7.15)

Постоянные времени Т₁ и Т₂ можно получить и из выражения для коэффициента ошибки по ускорению:

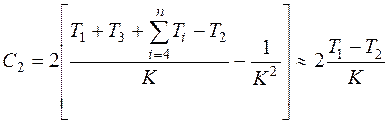. (7.16)

Упрощения в (7.16) не приводят к невыполнению требований по точности работы проектируемой системы РА. Из выражений (7.15) и (7.16) находим, что

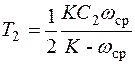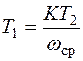, . (7.17)

Постоянную времени T₃ функции (7.6) определим из условия обеспечения в проектируемой системе запаса устойчивости (7.9):

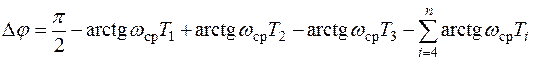. (7.18)

При высоких требованиях к точности работы системы не всегда можно удовлетворить заданные условия, используя функцию (7.6), поэтому приходится применять более сложную передаточную функцию (7.7). Коэффициент усиления в этом случае вычисляют по формуле (7.12), а постоянные времени T₁ и T₂ в соответствии с выражениями

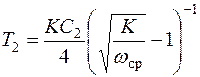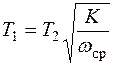; , (7.19)

тогда постоянную времени Т₃ рассчитывают по формуле

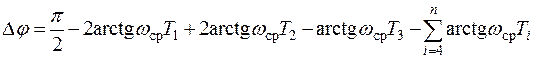.(7.20)

Аналогично определяются параметры желаемых передаточных функций статических систем РА (7.4) и (7.5) и систем с астатизмом 2-го порядка (7.8).

7.3 Определение передаточных функций корректирующих устройств

После выбора и определения параметров желаемой передаточной функции разомкнутой системы находят передаточные функции корректирующих устройств, предварительно определив передаточную функцию функционально необходимых устройств проектируемой системы. К таким устройствам относятся, например, фазовый детектор и перестраиваемый генератор в системе ФАПЧ, гетеродин и частотный дискриминатор в системе АПЧ, угловой дискриминатор и антенна с исполнительным устройством и усилителем мощности в системе автоматического сопровождения цели РЛС.