Определение. Областью устойчивости по параметрам будем называть множество матриц A, для которых выполняется общее условие устойчивости: .

Дата: 2025-05-25; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

На практике обычно речь идет об изменении одного - двух параметров системы.

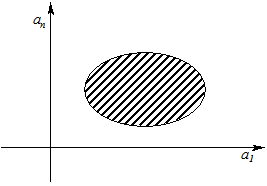
Рис. 5.15 - Область устойчивости системы

Определение. Критическими (граничными) будем называть такие значения матриц A, при которых система находится на границе устойчивости: Re λ(A)=0.

Определение. Запасом устойчивости называется диапазон значений параметра от номинального до граничного.

5.4.2 Частотные оценки запасов устойчивости

Частотные запасы устойчивости определяют в соответствии с критерием Найквиста амплитудно-фазовой характеристики разомкнутой системы от критической точки с координатами {-1, j0} (рис. 5.16).

Запас устойчивости по амплитуде (h) показывает, насколько можно увеличить амплитуду без потери устойчивости системы.

Запас устойчивости по фазе (γ) показывает, насколько можно изменить фазу системы без потери ею устойчивости.

Опытным путем установлено, что для нормальной работы система должна обладать следующими запасами устойчивости.

H=50-80 %, γ=50-80 %. (5.31)

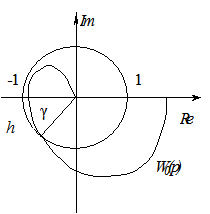
Рис. 5.16 - Определение запасов устойчивости по АФХ

Аналогичные запасы устойчивости можно определить по логарифмическим характеристикам системы.

Здесь запас устойчивости по модулю обозначают как ΔL и измеряют в децибелах [дБ]. Он определяется на частоте ω_КР, на которой фазовая частотная характеристика достигает значения –π. Запас устойчивости по фазе обозначают как Δφ, он определяется на частоте среза ω_СР, где ΔL=0 (рис. 5.17).

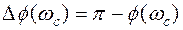. (5.32)

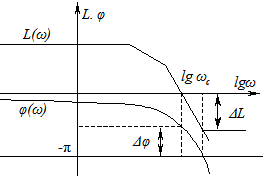
Рис. 5.17 - Определение запасов устойчивости по логарифмическим

характеристикам

Экспериментально установлено, что имея следующий запас устойчивости

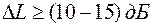
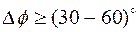, (5.33)

система будет работать удовлетворительно.

5.4.3 Корневые оценки запасов устойчивости

Склонность системы к неустойчивой работе выражается в большой колебательности процессов в ней, следовательно, процесс 2 на рис 5.18 соответствует системе с меньшим запасом устойчивости.

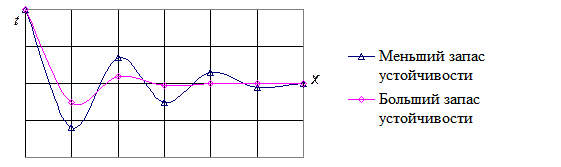
Рис. 5.18 - Процессы в системе с разным запасом устойчивости

Вид процессов в системе определяется корнями характеристического уравнения (5.4) (см. рис. 5.19), причем колебательный характер придают комплексно-сопряженные корни 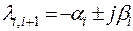, где вещественная часть (α_i) определяет скорость затухания, а мнимая часть корней (β_i) - частоту колебаний.

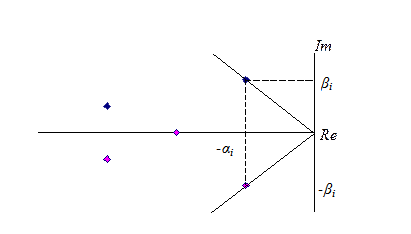
Рис. 5.19 - Распределение корней в системе

Пара корней с самым широким сектором будет давать составляющую процесса с наибольшими колебаниями, поэтому в качестве оценки устойчивости используем величину (5.34)

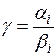, (5.34)

которая может изменяться в диапазоне 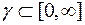. Чем меньше γ (т.е. больше мнимая часть корня), тем ближе система к границе устойчивости. При γ =0 она находится на границе устойчивости, если же γ=∞, система будет абсолютно устойчива.

Таким образом, корневая оценка запаса устойчивости γ характеризует, насколько можно изменять корни характеристического уравнения без потери устойчивости системой.

Обычно такая оценка используется на этапе проектирования, так как α трудно связать с параметрами реальной системы (коэффициентом усиления, постоянными времени, коэффициентом демпфирования).

5.4.4 Метод D-разбиения

На практике бывает необходимо знать не только запас, который можно оценить с помощью какого-либо критерия устойчивости, но и всю область устойчивости по параметрам. Этой цели служит метод D-разбиения, позволяющий построить такую область в плоскости одного или двух параметров.

Рассмотрим сначала этот метод для одного параметра D, который входит в характеристическое уравнение системы линейно

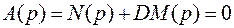. (5.35)

В (5.35) заменим p на jω и получим уравнение

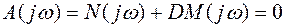, (5.36)

соответствующее границе устойчивости согласно критерию Михайлова (5.24). Разрешим его относительно D (5.37)

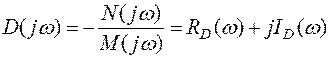. (5.37)

Полученное комплексное представление параметра D позволяет изобразить его в виде вектора на плоскости {R_D(ω);I_D(ω)}. Конкретное численное значение D(jω) зависит от частоты и при изменении ω в диапазоне от -∞ до +∞ конец вектора описывает на комплексной плоскости кривую D-разбиения, представляющую собой границу устойчивости (ее можно рассматривать так же, как отображение мнимой оси плоскости корней).

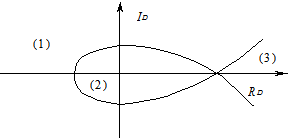
Рис. 5.20 - Иллюстрация построения кривой D-разбиения

Эта кривая симметрична относительно вещественной оси, поэтому достаточно построить ее часть, соответствующую положительным значениям частоты, а вторую часть получить зеркальным отображением относительно вещественной оси.

Кривая D разбивает плоскость параметра на несколько областей с различным условием устойчивости, для определения которого необходимо выбрать по одному значению D в каждой из них и проверить устойчивость с помощью какого-либо критерия. Если система устойчива при выбранном D, то она будет устойчива и при других значениях из этой области.

Обычно в качестве параметра D фигурирует реальный параметр системы (коэффициент усиления, постоянная времени, момент инерции и так далее), который может иметь только вещественные значения. Представление его комплексным выражением D(jω) носит формальный характер, а область устойчивости ограничивается отрезком вещественной оси.

Метод D-разбиения применим и в случае построения области устойчивости для двух параметров D₁ и D₂, которые входят линейно в характеристическое уравнение (5.38)

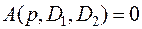. (5.38)

В этом случае уравнение границы устойчивости

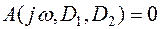(5.39)

распадается на два независимых уравнения, соответствующих равенству нулю вещественной и мнимой части (5.39):

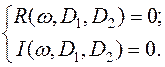(5.40)

Эти два уравнения параметрически задают кривую D-разбиения. Область устойчивости определяется аналогично случаю одного параметра D.