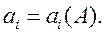Будем полагать, что известна передаточная функция разомкнутой системы
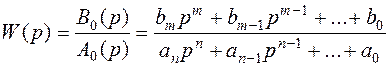, m≤n. (5.22)
Здесь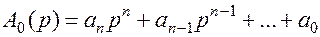 
- ее характеристический полином.
Структурная схема замкнутой системы имеет вид
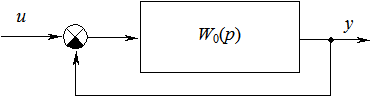
Рис. 5.11 - Структурная схема замкнутой системы
Передаточная функция замкнутой системы следующая:
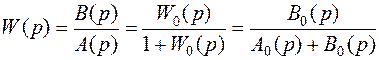, (5.23)
где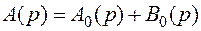 
- характеристический полином замкнутой системы.
Для получения критерия устойчивости вводится вспомогательная функция:
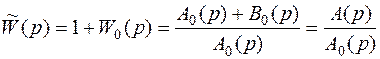. (5.24)
Как видим, числитель вспомогательной передаточной функции представляет собой характеристический полином замкнутой системы, а знаменатель - характеристический полином разомкнутой системы. Так как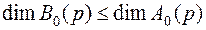 
, то в выражении для A(p) порядок суммы полиномов равен 
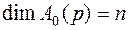. Следовательно, во вспомогательной передаточной функции 
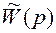полиномы числителя и знаменателя имеют один порядок (n).
В выражении (5.24) заменим р на jω и получим:
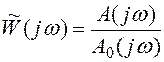. (5.25)
Рассмотрим результирующий угол поворота вектора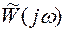 
при изменении ω от 0 до ∞, используя те же соотношения, что и при доказательстве критерия Михайлова.
Если замкнутая система устойчивая, то общее приращение фазы числителя (5.25) определяется как
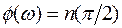. (5.26)
При устойчивой разомкнутой системе фаза в знаменателе будет иметь вид
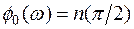. (5.27)
Результирующий угол поворота вектора 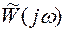равен разности (5.26) и (5.27).
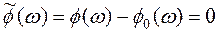. (5.28)
Таким образом, для устойчивости замкнутой системы (при устойчивой разомкнутой) должно выполняться соотношение (5.28). Это свойство имеет простую геометрическую интерпретацию: вспомогательная частотная характеристика не должна охватывать начало координат. Так как 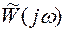отличается от 
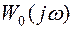на единицу, то можно строить амплитудно-фазовую характеристику разомкнутой системы, что значительно проще.
Формулировка критерия Найквиста. Для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика устойчивой разомкнутой системы при изменении ω от 0 до ∞ не охватывала точку с координатами {-1, j0}.
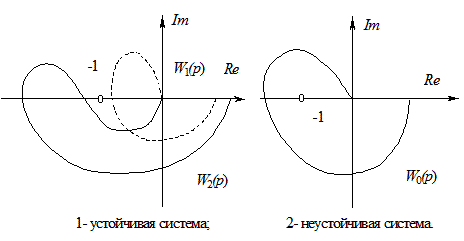
Рис. 5.12 - Частотные характеристики системы для критерия Найквиста
Разомкнутая система может быть неустойчива, но это не означает, что неустойчивой будет и замкнутая система. В этом случае меняется формулировка критерия Найквиста. Для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика неустойчивой разомкнутой системы при изменении ω от 0 до ∞ охватывала точку с координатами { - 1 j0} в положительном направлении r/2 раз, где r - число корней характеристического уравнения разомкнутой системы с положительной вещественной частью.
Критерий Найквиста можно также применять, если разомкнутая система имеет в своем составе интегратор, т.е. ее передаточная функция следующая:
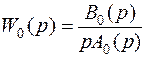. (5.29)
Полученная в результате замены р на jω в выражении (5.29) амплитудно-фазовая характеристика будет иметь неопределенность в точке ω= 0. Поэтому при ее построении делают аппроксимацию: характеристику дополняют полуокружностью бесконечно большого радиуса так, чтобы она начиналась на положительной вещественной полуоси (рис. 5.13).
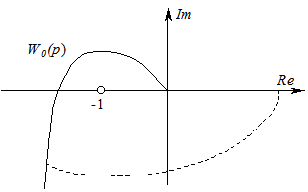
Рис. 5.13 - АФХ разомкнутой системы с интегратором
Замкнутая система будет находиться на границе устойчивости, если при некоторой частоте ω=ω0 АФХ разомкнутой системы пересекает точку с координатами {-1, j0}. Аналитически условие границы устойчивости записывается в виде:
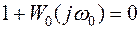. (5.30)
5.3.4 Логарифмическая форма критерия Найквиста
Для проверки устойчивости замкнутой системы можно использовать логарифмические частотные характеристики разомкнутой, которые строятся почти без вычислений. Правила построения ЛАЧХ см. п.3.5. с. 33.
Формулировка критерия Найквиста. Для замкнутой системы необходимо и достаточно, чтобы на частотах, где ЛАЧХ положительна (т.е. L (ω) > 0), фазовая частотная характеристика разомкнутой системы не пересекала ось - 1800 или пересекала ее четное число раз.
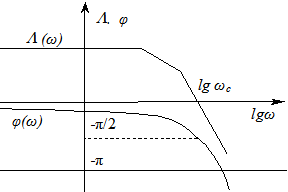
Рис. 5.14 - Логарифмические частотные характеристики,
иллюстрирующие критерий Найквиста
Замкнутая система будет находиться на границе устойчивости, если на той же частоте, где L (ω)=0, фазовая частотная характеристика разомкнутой системы пересекает ось – 180о.
5.4 Области и запасы устойчивости
5.4.1 Основные понятия и определения
Поскольку при составлении математической модели делается ряд допущений, то параметры реальной системы несколько отличаются от расчетных (номинальных). Кроме того, с течением времени они могут изменяться в некотором диапазоне, но при этом свойство устойчивости должно сохраняться. Поэтому для нормальной работы система должна обладать определенным запасом устойчивости.
Рассмотрим линейную стационарную систему общего вида, описываемую системой уравнений (5.1) и соответствующее ей характеристическое уравнение (5.4), которое имеет n корней 