Переходной процесс, возникающий в системе РА при воздействии единичного импульса, называют импульсной переходной функцией. Из выражения (3.15) следует, что

Дата: 2025-05-25; Просмотры: 4

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

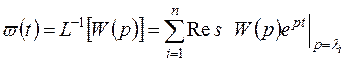. (3.16)

Импульсная переходная функция системы РА удовлетворяет следующим условиям

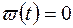при t<0, 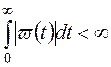. (3.17)

Первое условие называют условием физической реализуемости системы; оно показывает, что в реальной системе переходной процесс не может возникнуть раньше подачи на вход системы единичного импульса. Второе условие является условием устойчивости системы РА.

Согласно (3.9) и (3.15),

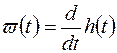. (3.18)

Интервал времени, на котором импульсная переходная функция отлична от нуля, называют памятью или инерционностью системы (рис. 3.2, а).

Импульсная переходная функция стационарной системы РА зависит только от разности времени наблюдения выходного сигнала и времени приложения к входу системы сигнала d-функции. В нестационарных системах РА импульсная переходная функция зависит не только от времени наблюдения, но и от времени возникновения входного сигнала (это происходит из-за изменения во времени параметров системы). Если на вход нестационарной системы подать в момент времени t₂ > t₁ сигнал вида d-функции, то импульсная переходная функция не только сдвинется по времени, как в случае стационарных систем (рис. 3.2, а), но и изменится по форме (рис. 3.2, б).

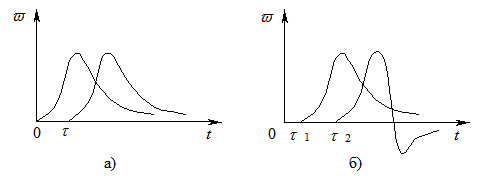
Рис. 3.2 - Импульсные переходные функции стационарной (а)

и нестационарной системы (б)

Условие физической реализуемости для нестационарных систем РА имеет вид 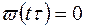при t < t . (3.19)

Пример. В качестве примера определим переходную и импульсную переходную функцию системы РА с передаточной функцией

.

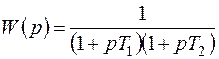Решение. Преобразование Лапласа для переходной функции находится по формуле (3.8):

,

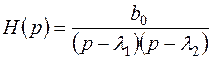где l₁, l₂ – полюсы системы; b₀ – постоянный коэффициент.

В соответствии с выражением (3.10)

.

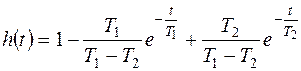Импульсная переходная функция, в соответствии с (3.16)

.

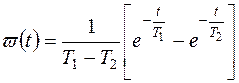Импульсная переходная функция может быть получена и из (3.18).

3.4 Выходной сигнал системы радиоавтоматики при произвольном воздействии

Из определения передаточной функции системы РА следует, что преобразования Лапласа для выходного сигнала при нулевых начальных условиях Y(p)=W(p) X(p).

На основании теоремы свертки сигнал на выходе будет иметь вид

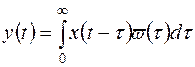. (3.20)

В нестационарных системах РА сигнал на выходе определяется как

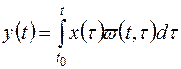, (3.21)

где t₀ – время подачи входного сигнала.

Выражения (3.20) и (3.21) позволяют определить выходной сигнал системы РА при произвольном виде входных сигналов.