11 – сурет. Сыртқы бағдарлау элементтерінің бірінші жүйесі.
Екінші жүйеде де алты сыртқы бағдарлау элементтері бар. Олардың үшеуі сызықтық, үшеуі бұрыштық. (12 сурет)
Сызықтық шамаларға проекция орталығының координаталары S Х0, Yо, Z0, жатады, ал бұрыштыққа:
α — сурет еңісінің бойлық бұрышы — Z осьі мен XZ жазықтығына негізгі сәуленің проекциясы арасындағы бұрыш ;
ω— сурет еңісінің көлденен бұрышы — негізгі сәле мен оның проекциясымен XZ жазықтығының арасындағы бұрыш, ол Y осьі мен негізгі сәуле арқылы өтетін жазықтықта орналасады;
æ — негізгі сәуле айналасында өзінің жазықтығында суреттің бұрылу бұрышы — у осьі мен У осьі мен негізгі сәуле арқылы өтетін жазықтықтағы іздің бұрышы.
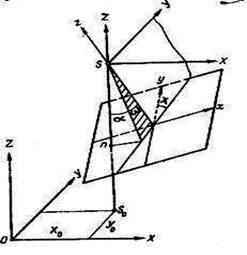
12– сурет. Сыртқы бағдарлау элементтерінің екінші жүйесі.
Сыртқы бағдарлау элементтері ұшу кезінде суретке түсіру моментінде анықталуы мүмкін, бірақ ірі масштабты картаграфиялауға жетіспейтін дәлділікпен. Сондықтан оларды анықтау үшін суретте танылған түсірілген жергілікті жердің бірнеше нүктелерінің геодезиялық координаталры болуы керек.
5. 10. Аумақтың сәйкес нүктелерінің координаталары мен олардың фототүсірістегі бейнелеріндегі координаталары арасындағы тәуелділік
13 суртте жергілікті жердің N нүктесінің басы болып, жергілікті жерде қабылданған NXYZ координата жүйесі көрсетілген.
n нүктесі мен N сәйкес келеді;
М нүктесі NXY жазықтығында болады;
S – проекция центрі;
P – сурет жазықтығы;
m – сурет жазықтығындағы жергілікті жердегі М нүктесінің бейнесі;
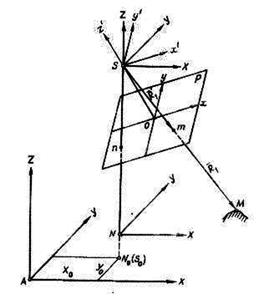
13–сурет. Жергілікті жердегі нүкте координаталары және олардың фотосуреттегі координаталар бейнелерінің арасындағы тәуелділік.
S нүктесінде екі координата жүйесі бар деп қарастырсақ:
1) SXYZ жергілікті жерде қабылданған, координата жүйесіне параллельді;
2) Sx’y’z’, где x’//x; y’//y; z’=z=-f.
Координаталарды түрлендіретің формулаларды қолданамыз.
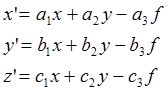- суреттің m нүкте координаталары,
мұнда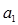 
, 
, 
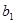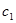- суреттің α, ω, χ, t, α0 , χ. бұрыштық бағдарлау элементтеріне бағынышты, косинус бағыттаушылыры,
Косинус бағыттауларын анықтауда SXYZ орналасу жағдайын басып қалу үшін Sx’y’z’ координата жүйелерінің үш бұрылуын жүргіземіз. Ол үшін ZX жазықтығында y’ осі айналасында α бұрышына, ZY жазықтығында x’ осін ω бұрышына, ал z’ті χ. бұрышына бұрады.
Мұндай бұрылысқа матрица қатысты болады
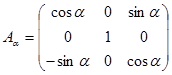
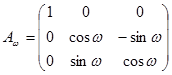- бұрылыс матрицасы
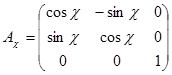
Матрицаның түрленуін табады
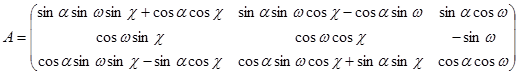
Матрицаның әрбір м үшесі арқылы белгілейтің болса, мынадай формула аламыз
,
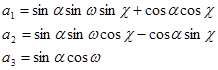
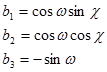
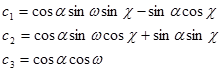Сонда аэрофотосуреттер үшін косинус баұыттаушыларын аламыз.
Егер косинус бағыттаушылары белгілі болса, онда α, ω, χ бұрыштарын формула бойынша табу5а болады:
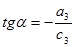
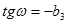
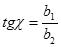
Sx’y’z’ координата жүйесіндегі m нүктесі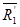 
векторымен 
, 
, 
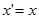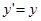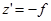координаталарымен анықталады.
SXYZ координата жүйесінде –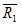 
векторымен X’Y’Z’ координаталарымен анықталады
Так как векторам 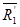мен 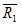вектормен коллинеарлыны болғандықтан 
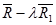, мұнда 
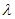- коэффициент немесе скаляр.
Бұл векторлардың компоненттері пропорциональды болғандықтан мынадай қылып жазуға болады:
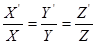, т.к.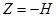 
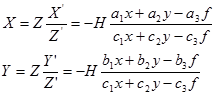сурет еністігі үшін
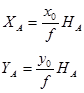горизонтальды сурет үшін
Егер суреттің бағдарлау элементтерінің үш белгісіз x, y, z нүктесінің нүктелері белгілі болса, жергілікті жердің әр бір нүктесіне мұндай теңдеулерді құруға болады. Бұдан шығатыны бір суреттің мәліметтері жергілікті жердің нүкте жағдайын анықтау үшін жеткіліксіз, бірақ суретке түсіру биіктігі H=Z белгілі боласа, нүкте координаталарының жергілікті жерін бір сурет бойынша табуға болады.
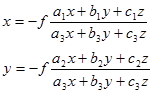
Суреттің нүкте координаталары мен жергілікті жердің нүкте координаталары арасындағы тәуелділік мына қатынастан алынады.
.
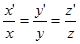