Урок 174-175 06.02.2023

Дата: 2025-06-14; Просмотры: 1
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Обратная связь: Вопросы присылать личным сообщением ВК.

1. Задание: самостоятельно поработать с видеоматериалом https://www.youtube.com/watch?v=NMVZU2Jn_OM, https://www.youtube.com/watch?v=OoR42yq4Lx4. Задачи по теме «Оптика», написать конспект.

Тема: Решение задач по теме «Оптика»

1.Пред­став­ле­на тон­кая линза, у ко­то­рой ука­за­на глав­ная оп­ти­че­ская ось, и ука­за­но, что в плос­ко­сти, про­хо­дя­щей через двой­ной фокус, рас­по­ла­га­ет­ся све­тя­ща­я­ся точка. Необ­хо­ди­мо опре­де­лить, какая из че­ты­рех точек на чер­те­же со­от­вет­ству­ет пра­виль­но­му изоб­ра­же­нию этого пред­ме­та, то есть све­тя­щей­ся точке.

За­да­ча может быть ре­ше­на несколь­ки­ми спо­со­ба­ми, рас­смот­рим два из них.

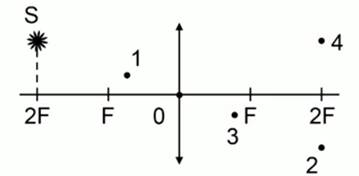
Рис. 1.

На рис. 1 изоб­ра­же­на со­би­ра­ю­щая линза с оп­ти­че­ским цен­том (0), фо­ку­сы ( 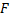), линза раз­но­фо­кус­ная и точки двой­но­го фо­ку­са ( 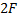). Све­тя­ща­я­ся точка ( 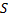) лежит в плос­ко­сти, рас­по­ло­жен­ной в двой­ном фо­ку­се. Необ­хо­ди­мо по­ка­зать, какая из че­ты­рех точек со­от­вет­ству­ет по­стро­е­нию изоб­ра­же­ния или изоб­ра­же­нию этой точки на схеме.

Ре­ше­ние за­да­чи нач­нем с во­про­са по­стро­е­ния изоб­ра­же­ния.

Све­тя­ща­я­ся точка ( 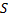) рас­по­ла­га­ет­ся на двой­ном рас­сто­я­нии от линзы, то есть это рас­сто­я­ние равно двой­но­му фо­ку­су, его можно по­стро­ить сле­ду­ю­щим об­ра­зом: взять линию, ко­то­рая со­от­вет­ству­ет лучу, дви­жу­ще­му­ся па­рал­лель­но глав­ной оп­ти­че­ской оси, пре­лом­лен­ный луч прой­дет через фокус ( 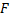), а вто­рой луч прой­дет через оп­ти­че­ский центр (0). Пе­ре­се­че­ние ока­жет­ся на рас­сто­я­нии двой­но­го фо­ку­са ( 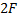) от линзы, это не что иное, как изоб­ра­же­ние, и оно со­от­вет­ству­ет точке 2. Пра­виль­ный ответ: 2.

Од­но­вре­мен­но с этим можно вос­поль­зо­вать­ся фор­му­лой тон­кой линзы и вме­сто 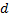под­ста­вить 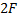, ведь точка лежит на рас­сто­я­нии двой­но­го фо­ку­са, при пре­об­ра­зо­ва­нии по­лу­чим, что изоб­ра­же­ние тоже по­лу­ча­ет­ся в точке, уда­лен­ной на двой­ном фо­ку­се, ответ будет со­от­вет­ство­вать 2 (рис. 2).

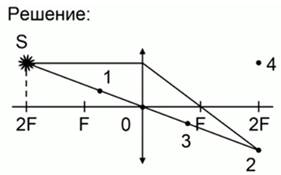
Рис. 2.

; ;

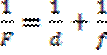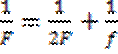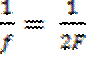
Ответ: 2.

  1. Пред­мет вы­со­той 3 сан­ти­мет­ра на­хо­дит­ся на рас­сто­я­нии 40 сан­ти­мет­ров от со­би­ра­ю­щей тон­кой линзы. Опре­де­лить вы­со­ту изоб­ра­же­ния, если из­вест­но, что оп­ти­че­ская сила линзы со­став­ля­ет 4 ди­оп­трии.

За­пи­сы­ва­ем усло­вие за­да­чи и, по­сколь­ку ве­ли­чи­ны ука­за­ны в раз­ных си­сте­мах от­сче­та, пе­ре­во­дим их в еди­ную си­сте­му и за­пи­шем урав­не­ния, необ­хо­ди­мые для ре­ше­ния за­да­чи:

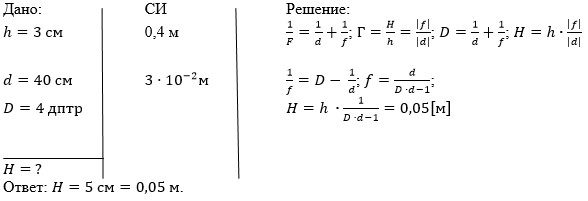
Мы ис­поль­зо­ва­ли фор­му­лу тон­кой линзы для со­би­ра­ю­щей линзы с по­ло­жи­тель­ным фо­ку­сом, фор­му­лу уве­ли­че­ния ( 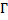) через ве­ли­чи­ну изоб­ра­же­ния и вы­со­ту са­мо­го пред­ме­та, а также через рас­сто­я­ние от линзы до изоб­ра­же­ния и от линзы до са­мо­го пред­ме­та. Вспом­нив, что оп­ти­че­ская сила ( 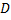) – это и есть об­рат­ное зна­че­ние фо­кус­но­го рас­сто­я­ния, можем пе­ре­пи­сать урав­не­ние тон­кой линзы. Из фор­му­лы уве­ли­че­ния за­пи­шем вы­со­ту изоб­ра­же­ния. Далее за­пи­шем вы­ра­же­ние для рас­сто­я­ния от линзы до изоб­ра­же­ния из пре­об­ра­зо­ва­ния фор­му­лы тон­кой линзы и за­пи­шем фор­му­лу, по ко­то­рой можно вы­чис­лить рас­сто­я­ние до изоб­ра­же­ния ( 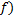. Под­ста­вив зна­че­ние 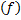в фор­му­лу вы­со­ты изоб­ра­же­ния, мы по­лу­чим необ­хо­ди­мый ре­зуль­тат 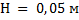, то есть вы­со­та изоб­ра­же­ния по­лу­чи­лась боль­ше, чем вы­со­та са­мо­го пред­ме­та. Сле­до­ва­тель­но, изоб­ра­же­ние дей­стви­тель­ное и уве­ли­че­ние боль­ше еди­ни­цы.

  1. Перед тон­кой со­би­ра­ю­щей лин­зой по­ме­сти­ли пред­мет, в ре­зуль­та­те та­ко­го раз­ме­ще­ния уве­ли­че­ние по­лу­чи­лось рав­ным 2. Когда пред­мет пе­ре­дви­ну­ли от­но­си­тель­но линзы, то уве­ли­че­ние стало равно 10. Опре­де­лить на сколь­ко пе­ре­дви­ну­ли пред­мет и в каком на­прав­ле­нии, если пер­во­на­чаль­ное рас­сто­я­ние от линзы до пред­ме­та со­став­ля­ло 6 сан­ти­мет­ров.

Для ре­ше­ния за­да­чи мы будем ис­поль­зо­вать фор­му­лу вы­чис­ле­ния уве­ли­че­ния и фор­му­лу со­би­ра­ю­щей тон­кой линзы.

Из этих двух урав­не­ний мы и будем ис­кать ре­ше­ние. Вы­ра­зим рас­сто­я­ние от линзы до изоб­ра­же­ния в пер­вом слу­чае, зная уве­ли­че­ние и рас­сто­я­ние. Под­ста­вив зна­че­ния в фор­му­лу тон­кой линзы, мы по­лу­чим зна­че­ние фо­ку­са 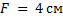. Далее все по­вто­ря­ем для вто­ро­го слу­чая, когда уве­ли­че­ние со­став­ля­ет 10. По­лу­чим рас­сто­я­ние от линзы до пред­ме­та во вто­ром слу­чае, когда пред­мет пе­ре­дви­ну­ли, 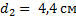. Мы видим, что пред­мет был пе­ре­дви­нут ближе к фо­ку­су, так как фокус со­став­ля­ет 4 сан­ти­мет­ра, в этом слу­чае уве­ли­че­ние со­став­ля­ет 10, то есть уве­ли­чи­ва­ет­ся изоб­ра­же­ние в 10 раз. Окон­ча­тель­ный ответ 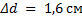, сам пред­мет был пе­ре­дви­нут ближе к фо­ку­су линзы и таким об­ра­зом уве­ли­че­ние стало боль­ше в 5 раз.

Далее прилагаются решения задач из методического пособия с подробным решением и рисунками к самим задачам.

  Далее рассмотрим задачи о плоских зеркалах.     1. Два плоских прямоугольных зеркала образуют двугранный угол φ=179°. На расстоянии l=10 см от линии соприкосновения зеркал и на одинаковом расстоянии от каждого зеркала находится точечный источник света. Определить расстояние d между мнимыми изображениями источника в зеркалах.

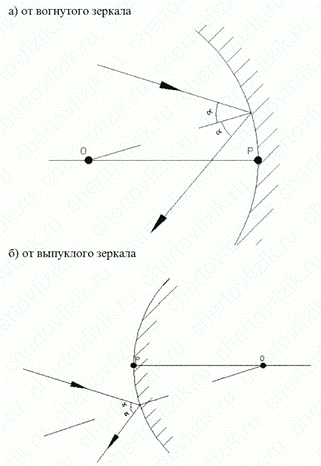
2. На сферическое зеркало падает луч света. Найти построе­нием ход луча после отражения в двух случаях:
а) от вогнутого зеркала;
б) от выпуклого зеркала.
На рисунке: P — полюс зеркала; O — оптический центр.

3. Вогнутое сферическое зеркало дает на экране изображение предмета, увеличенное в Г=4 раза. Расстояние a от предмета до зеркала равно 25 см. Определить радиус R кривизны зеркала.

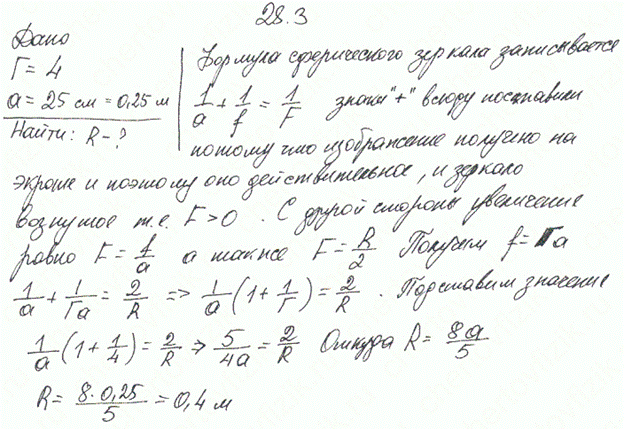
4. Фокусное расстояние f вогнутого зеркала равно 15 см. Зеркало дает действительное изображение предмета, уменьшенное в три раза. Определить расстояние a от предмета до зеркала.

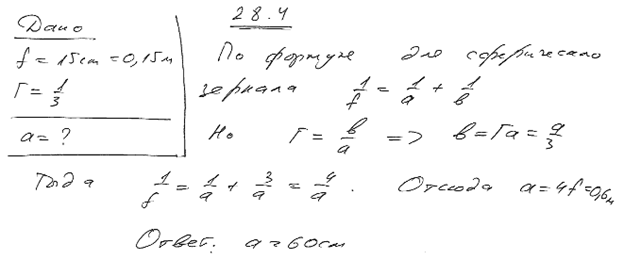
5. Радиус R кривизны выпуклого зеркала равен 50 см. Предмет высотой h=15 см находится на расстоянии a, равном 1 м, от зеркала. Определить расстояние b от зеркала до изображения и его высоту H.

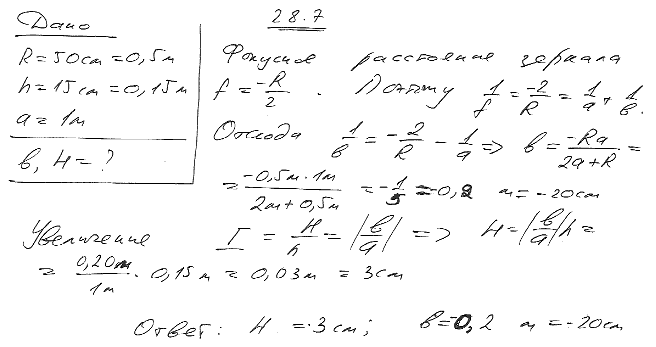
6. (28.45)Лупа дает увеличение Г=2. Вплотную к ней приложили собирательную линзу с оптической силой Ф1=20 дптр. Какое увеличение Г2 будет давать такая составная лупа?

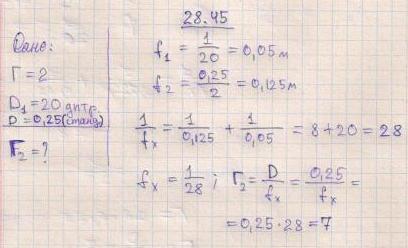
7. Оптическая сила Ф объектива телескопа равна 0,5 дптр. Окуляр действует как лупа, дающая увеличение Г1=10. Какое увеличение Г2 дает телескоп?

8. На собирающую линзу с фокусным расстоянием F1 = 40 см падает параллельный пучок лучей. Где следует поместить рассеивающую линзу с фокусным расстоянием F2 = 15 см, чтобы пучок лучей после прохождения двух линз остался параллельным?

Решение: По условию пучок падающих лучей ЕА параллелен главной оптической оси NN, после преломления в линзах он должен таковым и остаться. Это возможно, если рассеивающая линза расположена так, чтобы задние фокусы линз F1 и F2 совпали. Тогда продолжение луча АВ (рис. 7), падающего на рассеивающую линзу, проходит через ее фокус F2, и по правилу построения в рассеивающей линзе преломленный луч BD будет параллелен главной оптической оси NN, следовательно, параллелен лучу ЕА. Из рис. 7 видно, что рассеивающую линзу следует поместить на расстоянии d=F1-F2=(40-15)(см)=25 см от собирающей линзы.


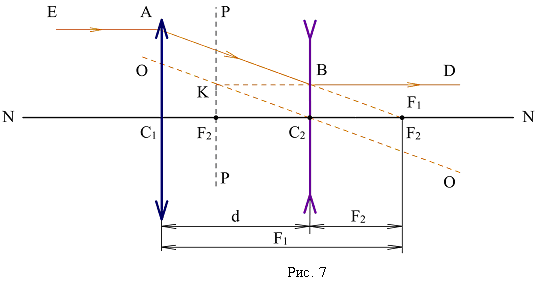
Ответ: на расстоянии 25 см от собирающей линзы.