Понятие правильного многогранника (тетраэдр, октаэдр, икосаэдр, куб, додекаэдр).
Определение. Выпуклый многогранник называется правильным, если все его грани равные правильные многоугольники и в каждой его вершине сходится одно и то же число рёбер.
Свойства.
· Все рёбра правильного многогранника равны друг другу;
· Все двугранные углы, содержащие две грани с общим ребром, равны.
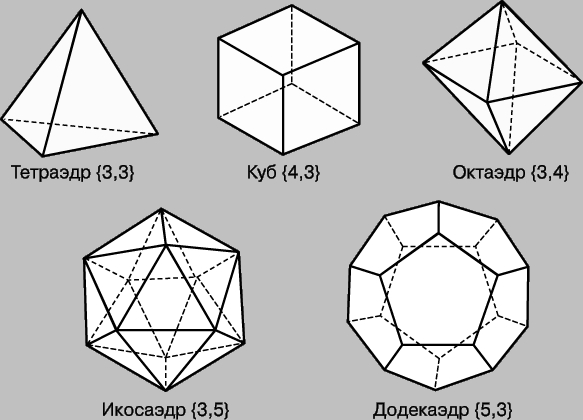
Существует только пять типов правильных многогранников:
· Правильный тетраэдр составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников. Следовательно, сумма плоских углов при каждой вершине равна 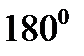 .
.
· Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх треугольников. Следовательно, сумма плоских углов при каждой вершине равна  .
.
· Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 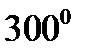 .
.
· Куб (гексаэдр) составлен из шести квадратов. Каждая вершина куба является вершиной трёх квадратов. Следовательно, сумма плоских углов при каждой вершине равна 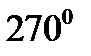 .
.
· Правильный додекаэдр составлен из двенадцати правильных пятиугольников.
Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Тогда сумма плоских углов при каждой вершине равна 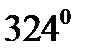 .
.
2. Теорема Эйлера.
Теорема Эйлера. Для числа граней Г, числа вершин В и числа рёбер Р любого выпуклого многогранника справедливо соотношение Г+В-Р=2.
Пусто n – число рёбер каждой грани, а m – число рёбер сходящихся в каждой вершине. Так как каждое ребро принадлежит двум граням, то nГ=2Р. Каждое ребро содержит по две вершины, значит mВ=2Р. Из последних двух равенств и теоремы Эйлера составим систему
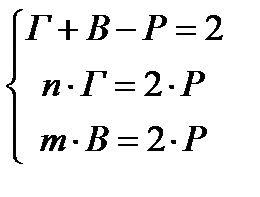 .
.
Решая эту систему, получим 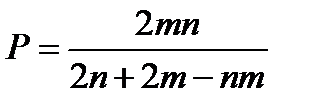 ,
, 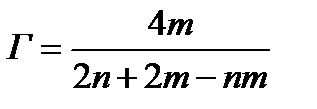 и
и 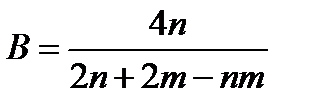 .
.
Найдём число вершин, рёбер и граней правильных многогранников:
· Правильный тетраэдр (n=3, m=3)
Р=6, Г=4, В=4.
· Правильный октаэдр (n=3, m=4)
Р=12, Г=8, В=6.
· Правильный икосаэдр(n=3, m=5)
Р=30, Г=20, В=12.
· Куб(n=4, m=3)
Р=12, Г=6, В=8.
· Правильный додекаэдр(n=5, m=3)
· Р=30, Г=12, В=20.








