Правильные многогранники. Элементы симметрии правильных многогранников».
16. 05. 2022 г. 10 класс.
Правильные многогранники. Элементы симметрии правильных многогранников».
Тип урока: урок применения знаний, умений и навыков учащихся.
Цели урока:
1. Образовательные: обобщение и систематизация сведений о правильных многогранниках и их элементов симметрии, применении симметрии в пространстве.
2. Развивающие:
Развитие умения логически излагать свои мысли, используя литературный язык;
Развитие умения аргументировать;
Развитие умения слушания и распределения внимания во время слушания;
Развитие умения задавать уточняющие вопросы;
Развитие умения полученные знания в нестандартных ситуациях;
Развивать умения выделять главное, сравнивать, обобщать;
Развитие абстрактного и наглядно-образного мышления.
3. Воспитательные: Воспитание любви к предмету, воспитание сознательной дисциплины, формирование навыков контроля и самоконтроля, активизация познавательной деятельности в коллективе и формирование навыков сотрудничества, межпредметная связь. Привитие чувств к прекрасному, эстетическое воспитание.
.
Изучение нового материала.
1) понятие симметричных точек относительно точки, прямой и плоскости.
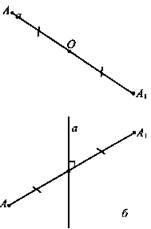
а) Точки А и A1 называются симметричными относительно точки О (центр симметрии), если О - середина отрезка АА1. Точка О считается симметричной самой себе.
Точки А и А1 называются симметричными относительно прямой а (ось симметрии), если прямая а проходит через середину отрезка АА1 и перпендикулярна к этому отрезку. Каждая точка прямой а считается симметричной самой себе.
Точки А и А1 называются симметричными относительно плоскости а (плоскость симметрии), если плоскость а проходит через середину отрезка АА1 и перпендикулярна к этому отрезку. Каждая точка плоскости а считается симметричной самой себе.
б) Итак, точка называется центром симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Если фигура имеет центр симметрии, то говорят, что она обладает центральной симметрией.
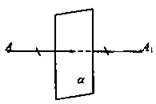
в) Прямая называется осью симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Если фигура имеет ось симметрии, то говорят, что она обладает осевой симметрией. .
г) Плоскость называется плоскостью симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Если фигура имеет плоскость симметрии, то говорят, что она обладает зеркальной симметрией.
Рисунки 84-85 учебника дают наглядное представление о рассматриваемых понятиях.
2) Понятие правильного многогранника
Выпуклый многогранник называется правильным, если все его грани - равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер.
Вопросы классу:
1) Какие вы знаете правильные многогранники?
2) Какие 2 условия определяют правильный многогранник?
3) Сколько может быть видов правильных многогранников?
На последний вопрос. Пусть при одной вершине сходится n ребер, тогда плоских углов при этой вершине будет тоже n, причем они все равны между собой. Пусть один из этих плоских углов равен α, тогда сумма плоских углов при вершине n · α, и по свойству плоских углов многогранного угла получим n · α < 360°, откуда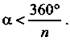 
Угол правильного n-угольника равен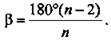 
Начиная с n = 7 плоский угол станет меньше 60°, а такого правильного многоугольника не существует.
1) Грани правильного многогранника - правильные треугольники, тогда р = 60°.
а) 60° · 3 = 180° < 360°. В этом случае правильный многогранник имеет 4 грани и называется правильным тетраэдром (рис. 81 учебника).
б) 60° · 4 = 240° < 360°. В этом случае правильный многогранник имеет 8 граней и называется правильным октаэдром (рис. 82 учебника).
в) 60° · 5 = 300° < 360°. В этом случае правильный многогранник имеет 20 граней и называется правильным икосаэдром (рис. 83 учебника).
г) 60° · 6 = 360°, это противоречит свойству о сумме плоских углов многогранного угла. Следовательно, больше правильных многогранников, грани которых - правильные треугольники, не существует.
2) Грани правильного многогранника - правильные четырехугольники (квадраты), тогда β = 90°.
а) 90° · 3 = 270° < 360°. В этом случае правильный многогранник имеет 6 граней и называется правильным гексаэдром (кубом) (рис. 84 учебника).
б) 90° · 4 = 360°, следовательно, больше правильных многогранников, грани которых квадраты, не существует.
3) Грани правильного многогранника - правильные пятиугольники, β = 108°.
а) 108° · 3 = 324° < 360°. В этом случае правильный многогранник имеет 12 граней и называется правильным додекаэдром (рис. 85 учебника).
б) 108° · 4 > 360°, следовательно, больше правильных многогранников, грани которых - правильные пятиугольники, не существует.
4) Начиная с правильного шестиугольника β ≥ 120°. Следовательно, n · β > 360° (n ≥ 3), поэтому правильных многогранников, грани которых - многоугольники с числом сторон больше 5, не существует.
Во время беседы учитель демонстрирует модели правильных многогранников, показывает рисунки параграфа.
Все эти типы многогранников были известны в Древней Греции - именно им посвящена завершающая, XIII книга «Начал» Евклида. Их называют также «платановыми телами» - они занимали видное место в идеалистической картине мира древнегреческого философа Платона. Четыре из них олицетворяют в ней четыре «сущности», или «стихии»: тетраэдр - огонь, икосаэдр - воду, куб - землю, октаэдр - воздух. Пятый же многогранник, додекаэдр, воплощал в себе «все сущее», символизировал все мироздание, почитался главнейшим. Уже по-латыни в средние века его стали называть «пятая сущность» или quinta essentia, «квинта эссенция», отсюда происходит слово «квинтэссенция», означающее все самое главное, основное, истинную сущность чего-либо.
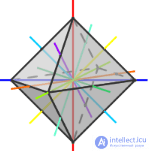
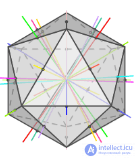
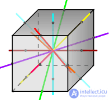
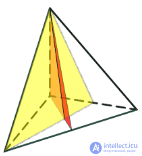
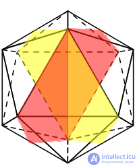
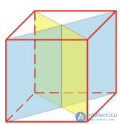
Таблица 1 - Элементы симметрии правильных многогранников
Тетраэдр
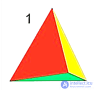
| Октаэдр
| Икосаэдр
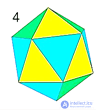
| Гексаэдр (куб)
| Додекаэдр
| |
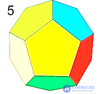
| Количество граней | 4 | 8 | 20 | 6 | 12 |
| количество ребер | 6 | 12 | 30 | 12 | 30 |
| вершин | 4 | 6 | 12 | 8 | 20 |
| Центры симметрии | - | 1 | 1 | 1 | 1 |
| Оси симметрии | 3 | 9 | 15 | 9 | 15 |
| 
| 
| 
| 
| |
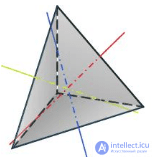
| Пло скости симметрии | 6 | 9 | 15 | 9 | 15 |
| 
| 
| 
| 
| |
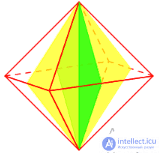
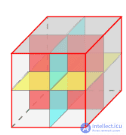
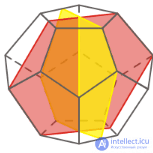
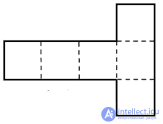
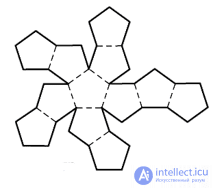
| Развертки |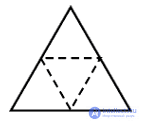 
| 
| 
| 
| 
|
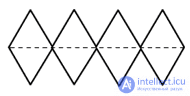
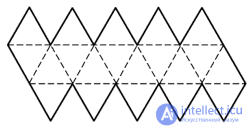
Решение задач
№ 279.
Дано: ABCDA1B1C1D1 - куб. А1В и A1C1 - диагонали граней куба, имеющие общий конец.
Найти: ∠ВА1С1.
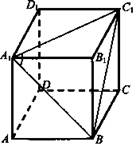
Решение:
1) Пусть а - ребро куба. Так как все грани куба - равные квадраты, то диагонали граней равны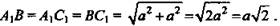 
2) ΔA1B1Q - равносторонний, значит, ∠BA1C1 = 60°. (Ответ: 60°.)
№ 281.
Дано: ABCDA1B1C1D1 - куб. D1A, D1C, D1B — диагонали граней.
Доказать: D1AB1C - правильный тетраэдр.
Найти: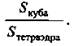 
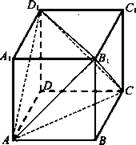
Решение:
1) Все грани куба - равные квадраты. Диагонали граней куба, являющиеся ребрами тетраэдра, равны. D1AB1C — правильный.
2) Пусть а - сторона куба. Значит, из ΔАВС: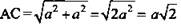 
- ребро тетраэдра.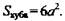 
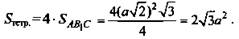
3) 
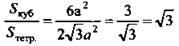(Ответ: √3.)
№ 287.
Дано: ABCDEF - правильный октаэдр; АВ = а.
Найти: a) BD; б) KL - расстояние между центрами двух смежных граней; в) НМ - расстояние между противоположными гранями.
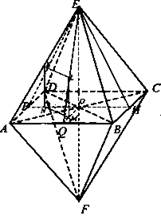
Решение:
а) Расстояние между противоположными вершинами для всех вершин одинаково. ΔABD - прямоугольный;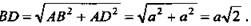 
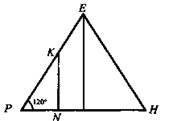
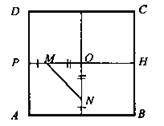
б) Расстояние между центрами двух смежных граней одинаково для всех смежных граней.
1) В грани DEA проведем высоту ЕР, в грани АЕВ проведем высоту EQ. Точки К, L - центры граней. KL - расстояние между центрами граней.
2) В плоскости РОЕ проводим KN ⊥ PO; в плоскости EQO проводим LM ⊥ QО. Тогда MN - проекция искомого отрезка KL на основание, KLMN - прямоугольник.
3) В ΔРЕН по теореме косинусов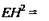 
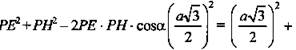
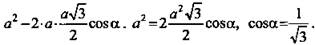ΔЕНВ - прямоугольный.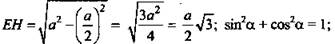 
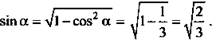
4) РК - радиус окружности, вписанной в правильный ΔEAD.
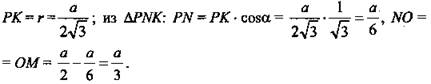
5) ΔNOM - прямоугольный и равнобедренный.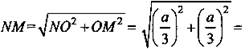 
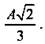Тогда 
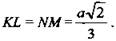
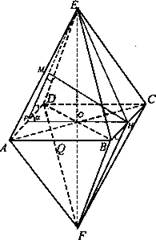
в) 1) Проведем через середину квадрата ABCD РН || АВ. FH ⊥ BC, EP ⊥ AD.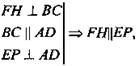 
грани AED и FBC параллельны
2) Плоскость (РЕН) ⊥ плоскости (FBC). В плоскости (РЕН) проведен отрезок MN ⊥ РЕ.
3) (РЕН) ⊥ AD ⇒ НМ ⊥ AD, НМ ⊥ РЕ, значит, MH ⊥ (AED) и МН ⊥ (FBC). Значит, НМ - искомое расстояние.
4) 
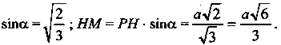
(Ответ: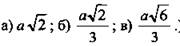 
)
I уровень.
№ 280 а.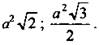 
II уровень
№ 283
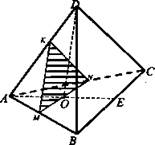
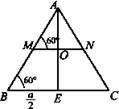
Решение: а) 1)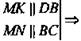 
плоскость MKN - искомое сечение.
2) 
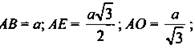
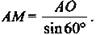
3) ΔADB - равносторонний, КМ || DB, значит, АМК - равносторонний,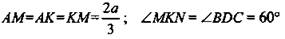 
(как углы с соответственно параллельными и одинаково направленными сторонами). 
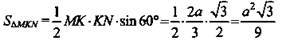(Ответ: 
)
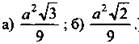№ 286
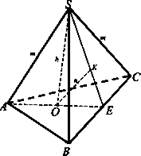
Решение:
1) ΔABC; AD - радиус описанной окружности. По теореме синусов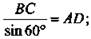 
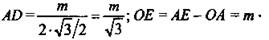
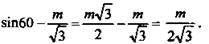
2) ΔAOS - прямоугольный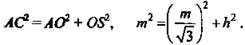 
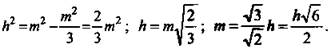б) OE = OK, значит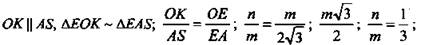 
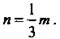(Ответ: 
)
.
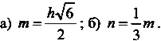2. Симметрия в природе.
«Раз, стоя перед чёрной доской и рисуя на ней мелом разные фигуры, я вдруг был поражён мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врождённое чувство, отвечал я сам себе. На чём же оно основано? Разве во всём жизни симметрия?» - задавал вопросы Николенька Иртеньев из «Отрочества» Л.Толстого.
Почему же в природе царит симметрия? Почему симметрично всё живое от микроорганизмов до человека?
Господство симметрии в природе объясняется силой тяготения, действующей во всей Вселенной. Действием тяготения или его отсутствие объясняется тем, что и космические тела, плавающие во Вселенной, и микроорганизмы, взвешенные в воде, обладают высшей формой симметрии – сферической (при любом повороте относительно центра фигуры совпадает сама с собой). Все организмы, растущие в прикреплённом состоянии (деревья) или живущие на дне океана (морские звёзды), т.е. организмы, для которых направление силы тяжести является решающим, имеют ось симметрии. Для животных способных передвигаться в воде, воздухе или по земле, кроме направления силы тяжести, важным оказывается и направление движения животного. Такие животные имеют плоскость симметрии. Биологи эту плоскость называют билатеральной, а тип симметрии – зеркальным.
Примеры симметрии в живой природе - насекомые, а именно, красивейшие создания земли – бабочки, которая являет собой пример зеркальной симметрии. Приложение 2.
Почти все кристаллы в природе – симметричны. Приложение 3.
3. Симметрия в искусстве ( архитектуре, скульптуре, живописи, литературе , музыке, танцах).
Наблюдая окружающий его мир, человек, исторически пытался более или менее реалистично отобразить его в различных видах искусства, поэтому очень интересно рассмотреть симметрию в живописи, скульптуре, архитектуре, литературе, музыке и танцах.
Симметрию в живописи мы можем увидеть уже в наскальных рисунках первобытных людей. В древние века значительной частью искусства рисования – были иконы, при создании которых художники использовали свойства зеркальной симметрии. Глядя на них сегодня, поражаешься удивительной симметричностью в обликах святых, хотя иногда происходит интересная вещь – в асимметричных изображениях мы ощущаем симметрию, как норму, от которой художник уклоняется под влиянием внешних факторов.
Элементы симметрии можно увидеть в общих планах зданий. Приложение 4. Скульптура и живопись тоже дают множество ярких примеров использования симметрии для решения эстетических задач. Примерами являются гробница Джулиано Медичи работы великого Микелланжело, мозаика апсиды собора Св. Софии в Киеве , где изображены две фигуры Христа, один причащает хлебом, другой – вином.
Зеркально – симметричное раздвоение фигуры Христа позволило одновременно изображать два важнейших момента евхаристии: причащение вином, обозначавшим кровь Христа. Зеркальное раздвоение Христа было одним из излюбленных приёмов иконографии тайной вечери. Приложение 5.
Симметрия, вытесняемая из живописи и архитектуры, постепенно занимала новые сферы жизни людей – музыку и танцы. Так в музыке 15 – ого века было открыто новое направление – имитационная полифония, являющаяся музыкальным аналогом орнамента, позже появились – фуги, звуковые версии сложного узора. В современном песенном жанре, как я считаю, припев – это пример простейшей переносной симметрии вдоль оси (текста песни). В танцах, использующих постоянно повторяющиеся фигуры и па, мы так же находим симметрию, смотрите на рисунок. Приложение 6.
Литература тоже не обошла своим вниманием симметрию. Так примером симметрии в литературе могут служить палиндромы, это такие части текста, обратная и прямая последовательность букв которых совпадают. Например, «А роза упала на лапу Азора» (А. Фет), «Уж редко рукою окурок держу». Как частный случай палиндромов, мы знаем много слов в русском языке, являющихся перевёртышами: кок, топот, казак и многие другие. На использовании таких слов часто строятся загадки – ребусы.
4. Правильные многогранники.
В геометрии фигура может иметь один или несколько центров симметрии (осей). Выпуклый многогранник называется правильным, если все его грани-равные правильные многогранники и в каждой его вершине сходится одно и то же число ребер. Примером правильного многогранника является куб.
Докажем, что не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще при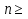 
6.
При 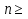6 угол каждого многоугольника больше или равен 120 
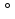. С другой стороны, при каждой вершине многогранника должно быть не менее трёх плоских углов. Но 120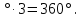 
По этой же причине каждая вершина правильного многогранника может быть вершиной 3, 4, 5 правильных треугольников, 3 квадратов или 3 правильных пятиугольников. Значит, есть только 5 правильных многогранников. Приложение 7.
1. Тетраэдр – четырёхгранник.
2. Гексаэдр – шестигранник (куб).
3. Октаэдр – восьмигранник.
4. Икосаэдр – двадцатигранник.
5. Додекаэдр - двенадцатигранник.
Правильные многогранники с древних времён привлекли к себе внимание учёных, архитекторов, художников.
Подробно описал свойства правильных многогранников древнегреческий учёный Платон. Поэтому их называют телами Платона. Правильным многогранникам посвящена 13 книга «Начал» Евклида. Платон считал, что атомы огня имеют форму тетраэдра, земли- гексаэдра, воздуха- октаэдра, воды- икосаэдра, вся вселенная – форму додекаэдра.
Герои картины испанского живописца С.Дали в «Тайной вечере» сидят на фоне огромного додекаэдра. Приложение 5. Художник А. Дюдер в гравюре «Меланхолия» дал перспективное изображение додекаэдра. Приложение 8.
В эпоху возрождения меланхолический темперамент отождествляли с творческим началом. На гравюре Дюрера Меланхолия окружена атрибутами зодчества и геометрии, отчего математики любят считать этот шедевр графического искусства олицетворением творческого духа математика, а саму Меланхолию – представительницей математики в мире прекрасного.
Повторение.