Графики зависимости относительной магнитной проницаемости
от намагничивающего поля Н
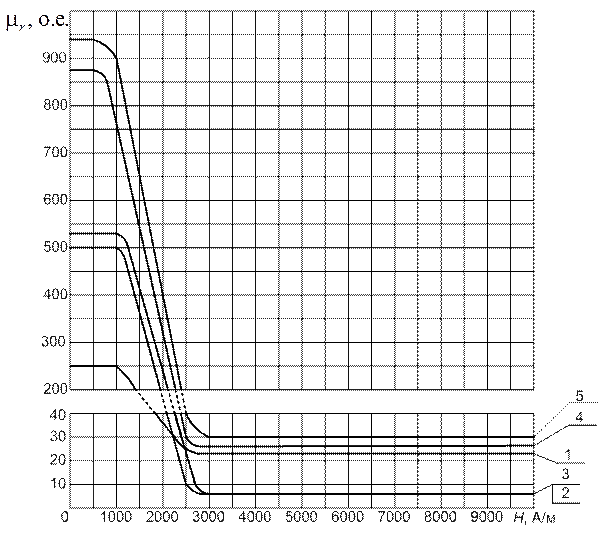
Рис. П1.11. Графики зависимости относительной магнитной проницаемости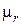 
от намагничивающего поля Н для конструкционных сплавов:
1 – серый чугун (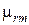 
= 215); 2 – ковкий чугун с черной сердцевиной ( = 500);
3 – ковкий чугун с белой сердцевиной ( 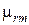= 530); 4 – сталь марки 20 ( 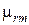= 880);
5 – сталь марки 30ХГС ( 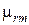= 940)
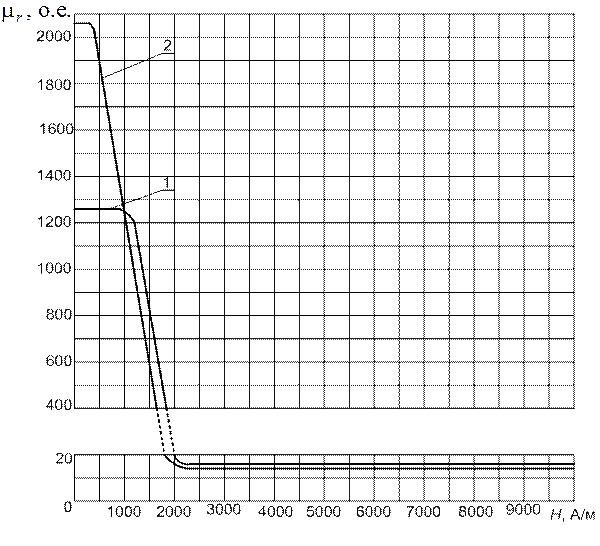
Рис. П1.12. Графики зависимости относительной магнитной проницаемости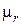
от намагничивающего поля Н для электротехнических холоднокатаных
изотопных сталей:
1 – марки 2421 ( 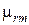= 1270); 2 – марки 2011 ( 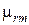= 2070)
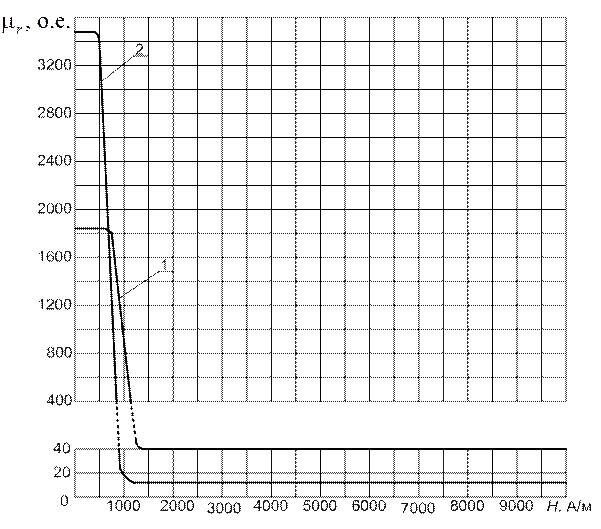
Рис. П1.13. Графики зависимости относительной магнитной проницаемости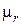
от намагничивающего поля Н для железокобальтовых сплавов
для концентраторов магнитного потока:
1 – сплав 27КХ ( 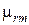= 1820); 2 – сплав 49К2Ф ( 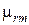= 3500)
7. Решение нелинейных уравнений
методом деления отрезка пополам
Суть метода состоит в следующем.
Пусть необходимо найти решение x = x0 некоторого уравнения
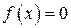(П1.10)
на некотором интервале области определения (x1; x2), содержащем решение, то есть x1 < x0 < x2 (рис. П1.14).
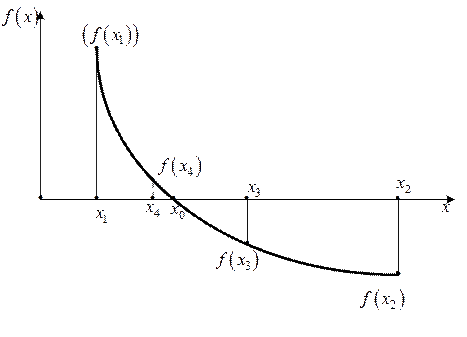
Рис. П1.14. Иллюстрация метода деления отрезка пополам
На первом этапе функция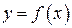 
исследуется на монотонность
в заданном интервале (x1; x2). Для этого вычисляется производная:
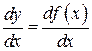(П1.11)
Если производная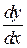 
не меняет знака (изменяется монотонно) в интервале (x1; x2), то можно с уверенностью сказать, что уравнение (П1.10) в интервале (x1; x2) имеет не более одного корня.
Как видно из графика, рис. П1.14, производная 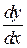– монотонно
отрицательна в интервале (x1; x2).
Далее метод деления отрезка пополам реализуется следующей последовательностью вычислительных процедур.
1. Вычисляется значение функции 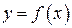в точках х1 и х2. В нашем случае 
; 
.
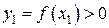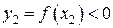2. Если значение y1 и y2 имеют разные знаки, т.е. y1y2 < 0, то вычисляется следующее приближение аргумента по формуле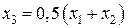 
.
3. Из графика функции 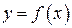видно, что 
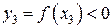. Таким образом, значения функци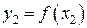и 
и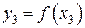 
имеют одинаковые знаки, т.е. y2y3 > 0, а значения функци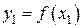и 
и 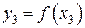имеют разные знаки, т.е. y1y3 < 0. Поэтому следующее приближение аргумента вычисляем по формуле 
.
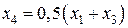4. Из графика функции 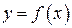видно, что 
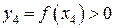. Таким образом y1y4 > 0, а y3y4 < 0. Поэтому очередное приближение аргумента х5 вычисляется по формуле 
.
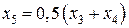5. Процедура последовательных приближений аргумента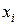 
к корню уравнения х0 по указанному алгоритму производится до выполнения условия
,
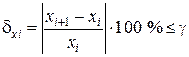где 
g – максимально допустимая погрешность определения значения корня х = х0 уравнения (П1.10).
Приложение 2