Форма трубки потока – половина прямого кругового цилиндра
Основанием трубки (рис. П1.2) является ребро а полуцилиндра. Стрелками показано направление вхождения магнитного потока в основание трубки.
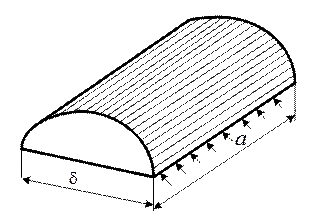
Рис. П1.2. Трубка потока в форме полуцилиндра:
а – высота цилиндра; d – диаметр цилиндра
Проводимость трубки определяется по формуле
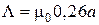. (П1.4)
Форма трубки потока – половина полого прямого кругового цилиндра
Основанием трубки (рис. П1.3) является прямоугольник с размерами сторон с и а. Стрелками показано направление вхождения магнитного потока в основании трубки.
Рис. П1.3. Трубка потока в форме половины полого цилиндра:
d – внутренний диаметр; с – толщина стенок; а – высота
Проводимость трубки определяется по формуле
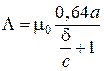. (П1.5)
Форма трубки потока – четверть шара
Основанием трубки (рис. П1.4) является вершина четверти шара. Стрелкой показано направление вхождения магнитного потока в основании трубки.
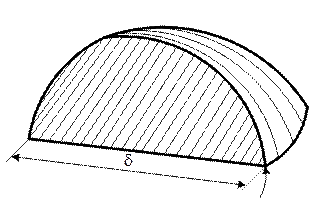
Рис. П1.4. Труба потока в форме четверти шара:
d – диаметр
Проводимость трубки определяется по формуле
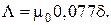(П.1.6)
Форма трубки потока – четверть сферической оболочки
Основанием трубки (рис. П1.5) является ребро вершины четверти сферической оболочки. Стрелками показано направление вхождения магнитного потока в основание трубки.
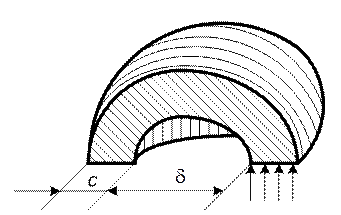
Рис. П1.5. Трубка потока в форме четверти сферической оболочки:
d – внутренний диаметр; с – толщина сферической оболочки
Проводимость трубки определяется по формуле
Λ=μ0 0,25с. (П1.7)
4. Определение проводимостей трубок магнитного потока
конца цилиндрического плужера, близкого к концу
концентрической трубки при m > e
Общий путь потока между плунжером и концентрической трубкой можно разбить на три участка, как показано на рис. П1.6. Для проводимости L'4 путь потока образован линиями индукции в форме концентрических дуг с центром в точке d.
Проводимость L'5 вычисляется на том основании, что путь потока образован линиями индукции в форме дуг с центром в точке a.
Проводимость L6 при m < r для удобства вычисления разбивается на три составляющие – L'6, L6'' и L6'''.
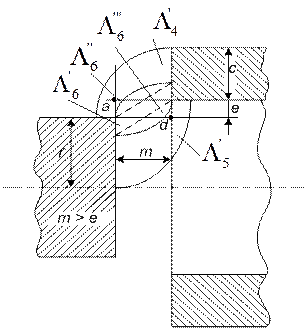
Рис. П1.6. Трубки потока цилиндрического плунжера,
близкого к концу концентрической трубки
Рассматривая центральную составляющую L'6, принимаем, что средняя длина пути потока равна m, а среднее сечение равно
.
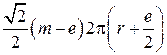Тогда при условии e << r, получим
L'6 = 4,45m0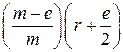 
.
Среднее сечение внешней составляющей проводимости равно
.
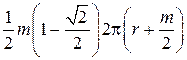Считая среднюю длину пути потока равной m, получаем
L6'' = 0,92m0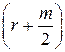 
.
Проводимость внутренней составляющей по аналогии равна
L6''' = 0,92m0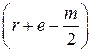 
.
Суммируя, получим полную проводимость для случая рис. П1.6.:
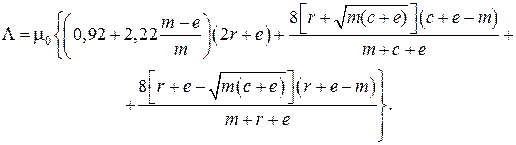(П1.8)
5. Определение проводимости трубки магнитного потока
между коаксиальными цилиндрами
Удельная на единицу длины проводимость Λ между коаксиальными цилиндрами, изображенными на рис. П1.7, определяется по формуле
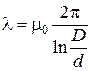. (П1.9)
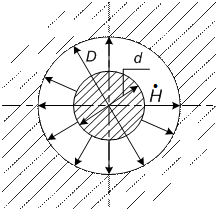
Рис. П1.7. К определению проводимости трубки магнитного потока
между коаксиальными цилиндрами:
D – диаметр наружного цилиндра; d – диаметр внутреннего цилиндра;
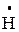– вектор магнитного поля в воздушном пространстве между цилиндрами
6. Магнитные характеристики магнитных материалов,
используемых для изготовления магнитопроводов магнитных систем
Основные кривые намагничивания
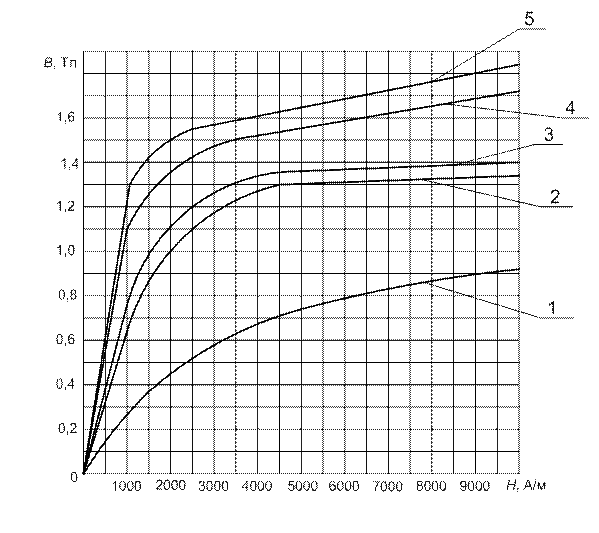
Рис. П1.8. Основные кривые намагничивания конструкционных сплавов:
1 – серый чугун (ГОСТ 1412-85); 2 – ковкий чугун с черной сердцевиной (ГОСТ 1215-79); 3 – ковкий чугун с белой сердцевиной (ГОСТ 1215-79); 4 – сталь марки 20
(ГОСТ 1050-88); 5 – сталь марки 30ХГС (ГОСТ 4543-71)
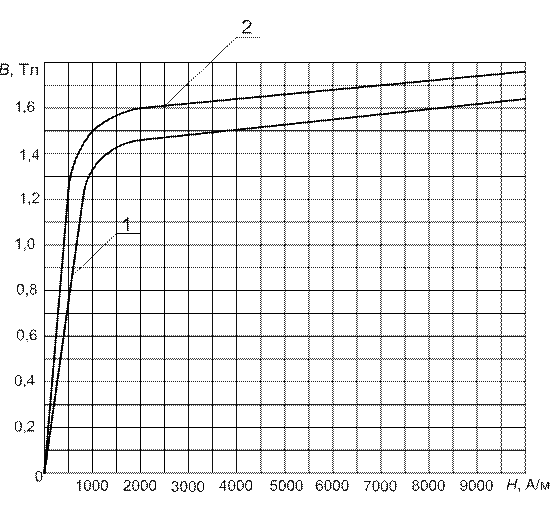
Рис. П1.9. Основные кривые намагничивания электротехнических
холоднокатаных изотропных сталей:
1 – марки 2421 (кремния 2,8-3,8 %) (ГОСТ 21427.2–83); 2 – марки 2011 (кремния
до 0,5 %) (ГОСТ 21427.2-83)
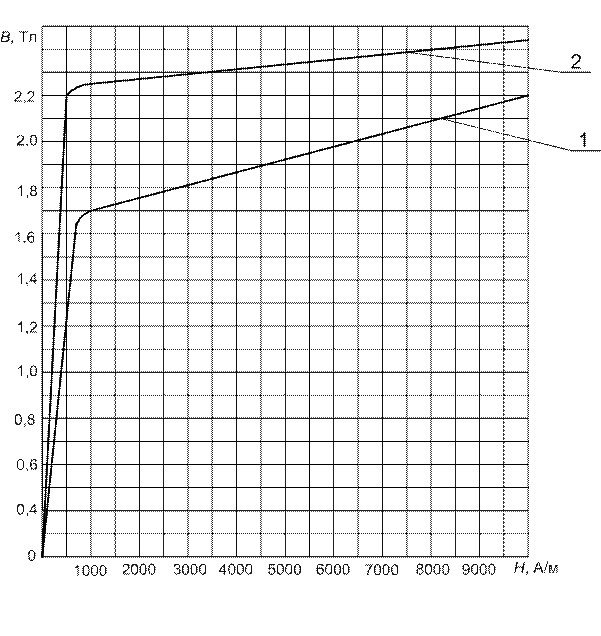
Рис. П1.10. Основные кривые намагничивания железокобальтовых сплавов
для концентраторов магнитного потока:
1 – сплав 27КХ; 2 – сплав 49К2Ф