Расчет магнитных систем
1. Методы теории магнитных цепей
При составлении математических моделей электромагнитов и устройств с постоянными магнитами (далее «магнитные системы») наиболее простыми и в то же время достаточно точными являются методы теории магнитных цепей. Суть этих методов состоит в том, что при расчете магнитных цепей используются уравнения, описывающие законы Ома и Кирхгофа для магнитных цепей, аналогичные тем, которые применяются при расчете электрических цепей. При этом используются аналогии физических параметров, приведенные в таблице П1.1
Таблица П1.1
Аналогии электрических и магнитных параметров,
используемые при анализе магнитных цепей
| № п/п | Параметр электрической цепи | Обозначение | Единица физ. величины | Параметр магнитной цепи | Обозначение | Единица физ. величины |
| 1 | Электрический ток | I | А | Магнитный поток | F | Вб |
| 2 | Электро-движущая сила (ЭДС) | E | В | Магнито-движущая сила (МДС) | M | А |
| 3 | Электрическое напряжение | U | В | Магнитное напряжение | Um | А |
| 4 | Электрическое сопротивление | R | Ом | Магнитное сопротивление | Rm | 1/Гн |
| 5 | Электрическая проводимость | L | 1/Ом | Магнитная проводимость | Lm | Гн |
С учетом данных табл. П1.1 уравнения, описывающие основные законы теории магнитных цепей, могут быть записаны в следующем виде.
Уравнение закона Ома для участков магнитной цепи:
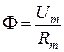 , (П1.1)
, (П1.1)
где F, Um и Rm – соответственно магнитный поток, магнитное напряжение и магнитное сопротивление участка магнитной цепи.
Уравнение первого закона Кирхгофа для узла магнитной цепи:
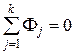 , (П1.2)
, (П1.2)
где Fj – j-й магнитный поток (со своим знаком); k – число ветвей магнитной цепи, сходящихся в данном узле.
Уравнение второго закона Кирхгофа для замкнутого контура магнитной цепи:
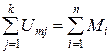 , (П1.3)
, (П1.3)
где Umj – магнитное напряжение на j-м участке замкнутого контура (со своим знаком); k – число участков контура, содержащих магнитное сопротивление; Mi – МДС i-го участка замкнутого контура (со своим знаком);
n – число источников МДС в контуре.
2. Метод определения проводимости воздушного зазора
магнитной системы по вероятным путям магнитного потока
При анализе магнитных систем наибольшую сложность в процессе составления математической модели представляет учет воздушных зазоров в магнитной цепи.
Реальная картина магнитного поля в воздушном зазоре магнитной системы и прилегающих областях достаточно сложна. Во многих случаях для реальных воздушных зазоров не удается получить строгого математического выражения, позволяющего вычислить их магнитные проводимости. Поэтому часто используется приближенный метод определения магнитных проводимостей воздушных зазоров по вероятным путям потока (метод Ротерса). При реализации этого метода используется понятие «Трубка магнитного потока».
Трубка магнитного потока – геометрическое тело в магнитном поле (рис. П1.1), имеющее два основания 1 и 2. В основание 1 входит магнитный поток F1, а из основания 2 выходит магнитный поток F2. Причем боковая поверхность 3 построена так, что силовые линии магнитного поля ее не пронизывают, т.е. вектор магнитного поля 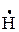 всегда параллелен поверхности трубки магнитного потока. Поэтом для любой магнитного трубки потока справедливо неравенство F1 = F2.
всегда параллелен поверхности трубки магнитного потока. Поэтом для любой магнитного трубки потока справедливо неравенство F1 = F2.
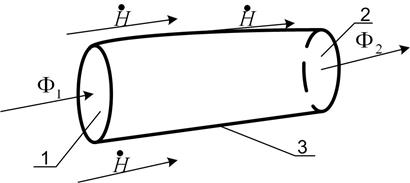
Рис. П1.1. Трубка магнитного потока:
1 – основание входа магнитного потока Ф1; 2 – основание выхода магнитного
потока Ф2; 3 – боковая поверхность
Метод Ротерса состоит в следующем. Реальное магнитное поле в пространстве воздушного зазора и прилегающей области заменяется упрощенным аналогом. Для этого рассматриваемая область разбивается на простые геометрические фигуры, которые представляют собой трубки магнитного потока (вероятные пути потока). Для каждой из таких трубок определяют магнитную проводимость по одной из следующих формуле
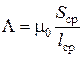 ;
;
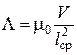 ,
,
где μ0 – магнитная постоянная, μ0 = 4p10–7 Гн/м; Sср и lср – среднее значение соответственно поперечного сечения и длины трубки потока; V – объем трубки магнитного потока.
Магнитные проводимости отдельных вероятных путей потока используются для вычисления полной магнитной проводимости воздушного зазора.
3. Определение проводимостей простейших трубок
вероятных путей магнитного потока








