R ш2 , R ш3 и их округленных значений R ш1(0), R ш2(0), R ш3(0).
Значения сопротивлений резисторов Rш1, Rш2 и Rш3 определяются по формулам (4.10) – (4.15).
При округлении считается, что 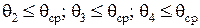 . Эти условия с учетом формул (4.17) – (4.19) можно записать в виде:
. Эти условия с учетом формул (4.17) – (4.19) можно записать в виде:
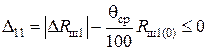 ; (4.36)
; (4.36)
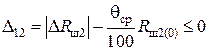 ; (4.37)
; (4.37)
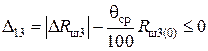 . (4.38)
. (4.38)
4.6.4. Определение значений резисторов R ш1(р), R ш2(р), R ш3(р)
Значения сопротивлений резисторов Rш1(р), Rш2(р) и Rш3(р) из ряда предпочтительных значений (прил. 4), ближайших к соответствующим округленным значениям сопротивлений Rш1(0), Rш2(0) и Rш3(0), определяются по формулам (4.26) – (4.28) с учетом неравенств 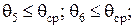
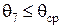 .
.
После подстановки и преобразования получаем неравенства для выбора значений сопротивлений Rш1(р), Rш2(р), Rш3(р):
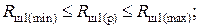 (4.39)
(4.39)
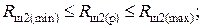 (4.40)
(4.40)
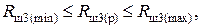 (4.41)
(4.41)
где 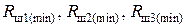 и
и 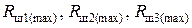 – соответственно наименьшие и наибольшие допустимые значения сопротивлений Rш1(р), Rш2(р), Rш3(р), определяемые из выражений:
– соответственно наименьшие и наибольшие допустимые значения сопротивлений Rш1(р), Rш2(р), Rш3(р), определяемые из выражений:
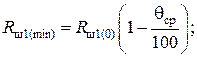 (4.42)
(4.42)
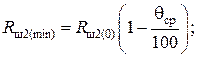 (4.43)
(4.43)
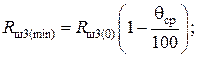 (4.44)
(4.44)
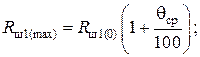 (4.45)
(4.45)
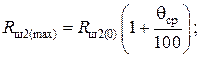 (4.46)
(4.46)
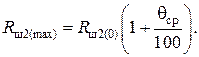 (4.47)
(4.47)
Если в рядах предпочтительных значений нет сопротивлений, удовлетворяющих условиям (4.39) – (4.41), то из рядов предпочтительных значений сопротивлений выбираются ближайшие значения сопротивлений по условиям (4.39), (4.40) и (4.41). Они рассматриваются как основные в композиции из двух последовательно включенных резисторов. Дополнительные резисторы в каждой паре резисторов выбираются из условий (4.32) – (4.34).
4.6.5. Выбор стандартного допустимого отклонения
значений сопротивлений
Стандартные допустимые отклонения 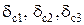 значений сопротивлений соответственно Rш1, Rш2 и Rш3 выбирают из прил. 4. Поскольку, как указывалось ранее, границы относительных погрешностей
значений сопротивлений соответственно Rш1, Rш2 и Rш3 выбирают из прил. 4. Поскольку, как указывалось ранее, границы относительных погрешностей 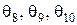 определяются допусками
определяются допусками 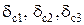 , справедливы равенства:
, справедливы равенства:
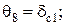 (4.48)
(4.48)
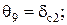 (4.49)
(4.49)
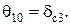 (4.50)
(4.50)
При выборе значений допусков 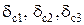 обязательным условием является выполнение следующих неравенств:
обязательным условием является выполнение следующих неравенств:
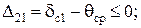 (4.51)
(4.51)
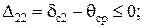 (4.52)
(4.52)
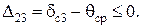 (4.53)
(4.53)
4.6.6. Определение действительного значения границы
не исключенной основной систематической погрешности 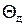
Значение 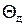 определяется по формуле (4.16).
определяется по формуле (4.16).
Границы относительных погрешностей 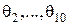 определяются соответственно по формулам (4.17) – (4.19), (4.26) – (4.28), (4.48) – (4.50).
определяются соответственно по формулам (4.17) – (4.19), (4.26) – (4.28), (4.48) – (4.50).
Условием обеспечения необходимой точности измерения проектируемого микроамперметра является выполнение неравенства
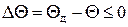 . (4.54)
. (4.54)
4.7. Пример проектного расчета трехпредельного
стрелочного микроамперметра постоянного тока
Расчет проводится в соответствии с алгоритмом, схема которого изображена на рис. 4.5.
Блок 1: 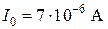 ;
;
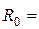 1000 Ом;
1000 Ом;
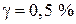 ;
;
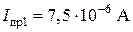 ;
;
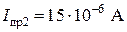 ;
;
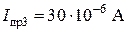 ;
;
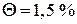 ;
;
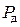 = 0,95 о.е.
= 0,95 о.е.
Блок 2: 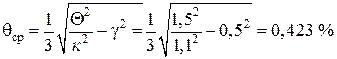 .
.
Блок 3: 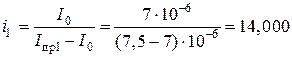 о.е.;
о.е.;
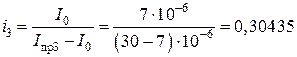 о.е.;
о.е.;
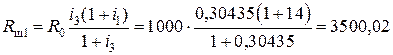 Ом.
Ом.
Блок 4: 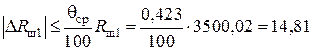 Ом;
Ом;
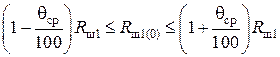 ;
;
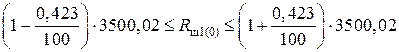 ;
;
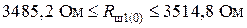 .
.
К найденному диапазону ближе всего значение 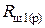 = 3480,0 Ом (прил. 4, п. 2, табл. П4.2). Поэтому выбираем ближайшее к нему значение
= 3480,0 Ом (прил. 4, п. 2, табл. П4.2). Поэтому выбираем ближайшее к нему значение
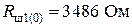 ,
,
уточняем значение 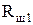 :
:
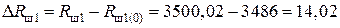 (Ом);
(Ом);
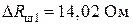 .
.
Блок 5: 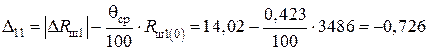 (Ом).
(Ом).
Блок 6: 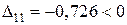 .
.
Блок 7: 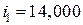 ;
; 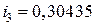 ;
;
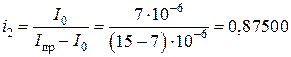 ;
;
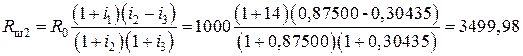 Ом.
Ом.
Блок 8: 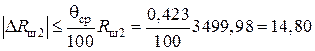 Ом;
Ом;
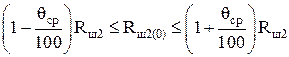 ;
;
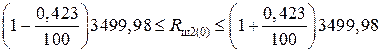 ;
;
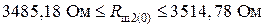 .
.
По аналогии с 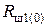 выберем
выберем
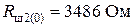 ,
,
и уточним значение 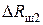 :
:
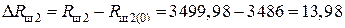 Ом;
Ом;
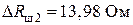 .
.
Блок 9: 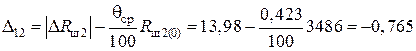 .
.
Блок 10: 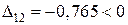 .
.
Блок 11: 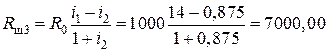 Ом.
Ом.
Блок 12: 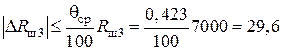 Ом;
Ом;
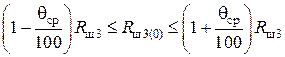 ;
;
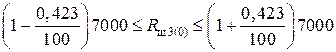 ;
;
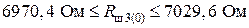 .
.
В найденный диапазон входит значение 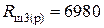 Ом (прил. 4, п. 2, табл. П4.2). Поэтому выбираем
Ом (прил. 4, п. 2, табл. П4.2). Поэтому выбираем 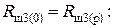
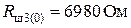 ,
,
уточняем значение 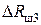 :
:
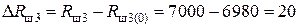 Ом;
Ом;
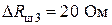 .
.
Блок 13: 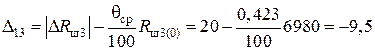 .
.
Блок 14: 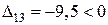 .
.
Блок 15: 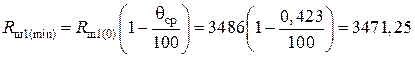 Ом;
Ом;
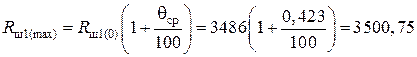 Ом.
Ом.
Блок 16: 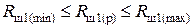 ;
;
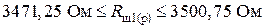 .
.
Блок 17: 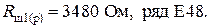
Блок 19: 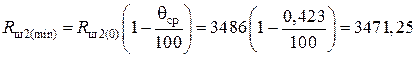 Ом;
Ом;
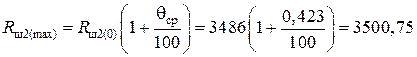 Ом.
Ом.
Блок 21: 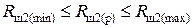 ;
;
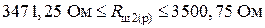 .
.
Блок 23: 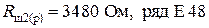 .
.
Блок 25: 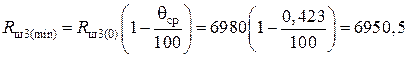 Ом;
Ом;
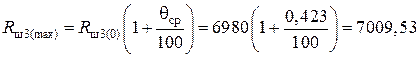 Ом.
Ом.
Блок 28: 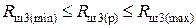 ;
;
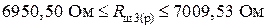 .
.
Блок 29: 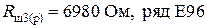 .
.
Блок 30: 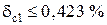 ; из ряда прил. 4, п. 1 выбираем ближайшее значение
; из ряда прил. 4, п. 1 выбираем ближайшее значение 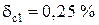 .
.
Блок 32: 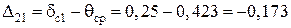 .
.
Блок 35: 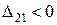 .
.
Блок 36: 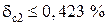 ; из ряда прил. 4, п. 1 выбираем ближайшее значение
; из ряда прил. 4, п. 1 выбираем ближайшее значение 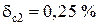 .
.
Блок 37: 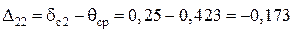 .
.
Блок 38: 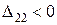 .
.
Блок 39: 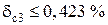 ; из ряда прил. 4, п. 1 выбираем ближайшее значение
; из ряда прил. 4, п. 1 выбираем ближайшее значение 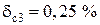 .
.
Блок 40: 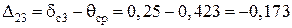 .
.
Блок 41: 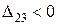 .
.
Блок 42: 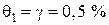 .
.
Блок 43: 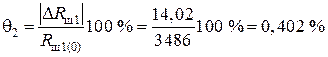 .
.
Блок 44: 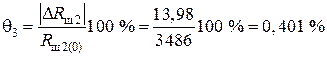 .
.
Блок 45: 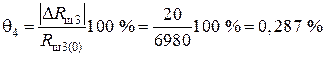 .
.
Блок 46: 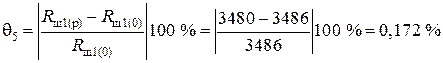 .
.
Блок 47: 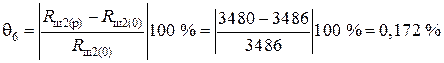 .
.
Блок 48: 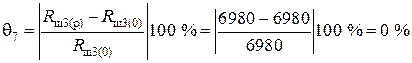 .
.
Блок 49: 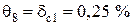 .
.
Блок 50: 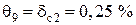 .
.
Блок 51: 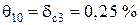 .
.
Блок 52: 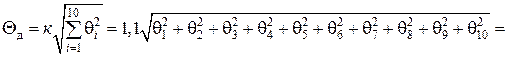
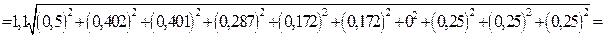
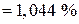 .
.
Блок 53: 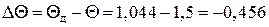 .
.
Блок 54: 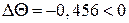 .
.
Примечание. Учитывая, что значение отклонения 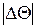 велико (
велико ( 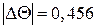 ), попробуем снизить требования к стандартному допустимому отклонению значений сопротивлений резисторов
), попробуем снизить требования к стандартному допустимому отклонению значений сопротивлений резисторов 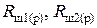 и
и 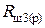 от их номинального значения.
от их номинального значения.
Из ряда прил. 4, п. 1 выбираем большее стандартное отклонение 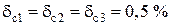 , следовательно,
, следовательно, 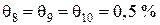 .
.
При этих значениях 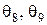 и
и 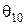 в соответствии с процедурой Блока 52 получим значение
в соответствии с процедурой Блока 52 получим значение 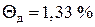 .
.
Условие обеспечения измерения микроамперметра с требуемой точностью обеспечивается:
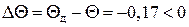 .
.
Блок 55: Вывод результатов:
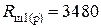 Ом; ряд Е48;
Ом; ряд Е48; 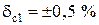 ;
;
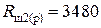 Ом; ряд Е48;
Ом; ряд Е48; 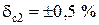 ;
;
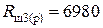 Ом; ряд Е48;
Ом; ряд Е48; 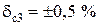 ;
;
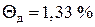 .
.








