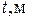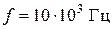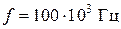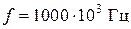Тема 2. Построение математической модели дифференциального трансформаторного индуктивного преобразователя прямоходного типа
2.1. Описание моделируемого объекта
Моделируемый дифференциальный трансформаторный индуктивный преобразователь прямоходного типа (далее «ДТИП») схематически изображен на рис. 2.1. ДТИП состоит из подвижного цилиндрического магнитного якоря 1, перемещающегося внутри электроизоляционного (пластикового) каркаса 6 катушки в направлении оси его симметрии. На каркасе катушки равномерно размещена первичная обмотка (обмотка возбуждения) 3 с числом витков N1, разбитая на две одинаковых полуобмотки с числом витков N1/2 каждая. Поверх первичной обмотки размещены две вторичные (индуктивные) обмотки: верхняя 4 и нижняя 5 с одинаковым числом витков N2 каждая, соединенные последовательно встречно.
Вся конструкция помещена в кожух 2 из магнитомягкого материала. Кожух выполняет несущую и защитную функции, но главным его назначением является замыкание магнитного потока якоря F0 вокруг катушки.
При подаче на первичную обмотку 3 переменного напряжения U, которое будем называть напряжением питания, во вторичных обмотках 4 и 5 наводится соответственно ЭДС Е1 и ЭДС Е2. В реальных ДТИП эти ЭДС выпрямляются и сглаживаются. Если геометрический центр якоря 1 находится в геометрическом центре катушки с обмотками 3, 4 и 5, то ЭДС, наведенные в обмотках 4 и 5, одинаковы (Е1 = Е2). Их разностный выпрямленный сигнал ΔЕ = Е1 – Е2 равен нулю. При перемещении якоря, например вверх на величину D, изменяется конфигурация магнитной системы, так что степень взаимной индуктивной связи обмотки 3 с обмоткой 4 увеличится, а с обмоткой 5 уменьшится. При этом разностный сигнал ΔЕ
будет положительным (ΔЕ = Е1 – Е2 >0).
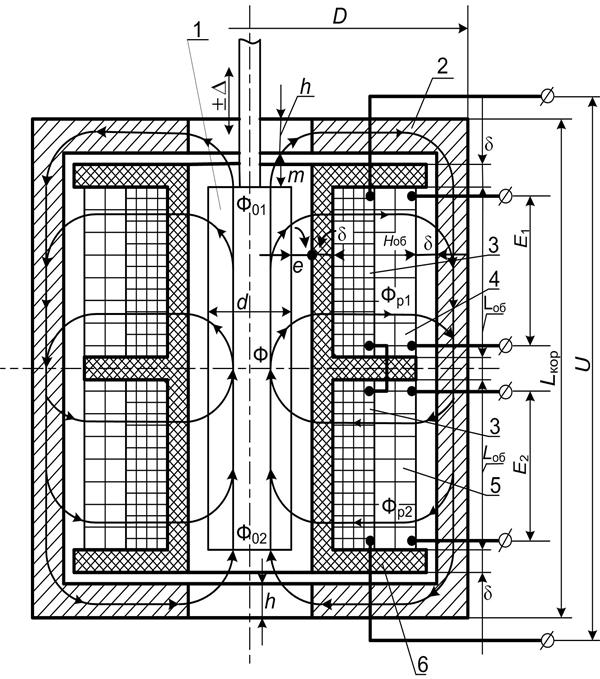
Рис. 2.1. Моделируемый ДТИП:
1 – подвижный якорь из магнитомягкого материала; 2 – кожух из магнитомягкого материала; 3 – две полуобмотки первичной электрической обмотки (обмотка возбуждения); 4 и 5 – две вторичные электрические индуктивные обмотки; 6 – каркас катушки из электроизоляционного материала
С увеличением перемещения D значение сигнала DЕ будет возрастать. Если якорь переместится вниз от геометрического центра, то степень взаимоиндуктивной связи обмотки 3 с обмоткой 4 уменьшится, а с обмоткой 5 увеличится. При этом разностный сигнал DЕ станет отрицательным (DЕ < 0) и с увеличением перемещения D значение сигнала DЕ будет уменьшаться.
ДТИП предназначен для преобразования линейного перемещения якоря в напряжение. Функция преобразования ДТИП имеет вид
ΔЕ = f(Δ). (2.1)
Она является практически линейной функцией типа
DЕ = SD, (2.2)
где S – чувствительность ДТИП, в относительно небольшой области определения аргумента D.
Область определения аргумента функции (2.2) ограничивается неравенством
|D| £ Dлин, (2.3)
где Dлин – граница линейности функции (2.2).
Выход значений аргумента D за пределы области определения (2.3) приводит к проявлению нелинейности функции (2.1), благодаря краевым эффектам.
2.2. Задание на выполнение практической работы
Цель работы:
– построить математическую модель ДТИП;
– рассчитать функцию преобразования ДТИП и определить его чувствительность при заданных конструктивных параметрах.
2.2.1. Этапы построения математической модели ДТИП
Построение математической модели ДТИП необходимо выполнять в предлагаемой последовательности.
Этап 1. На основании анализа распределения магнитных потоков в ДТИП составить магнитную цепь, моделирующую его магнитную систему.
При подаче переменного напряжения U на первичную обмотку 3 (рис. 2.1) в последней возникает ток, создающий полный магнитный поток F в якоре 1. Однако благодаря наличию магнитного напряжения в рабочих воздушных зазорах между якорем 1 и кожухом 2 одна часть потока F, называемая магнитным потоком рассеивания Fр, замыкается между якорем и стенками кожуха, а другая его часть F0, называемая основным магнитным потоком, замыкается между якорем и кожухом через рабочие воздушные зазоры.
Если геометрический центр якоря находится в геометрическом центре катушки, то справедливы равенства:
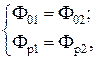(2.4)
где 
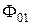и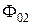 
– основные магнитные потоки соответственно верхней и нижней части ДТИП; 
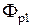и 
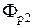– магнитные потоки рассеивания соответственно верхней и нижней части ДТИП.
Если якорь сместится, например, вверх на величину Δ, то равенства (2.4) преобразуются в систему неравенств:
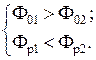(2.5)
Это связано с тем, что указанное перемещение D приведет к уменьшению магнитного сопротивления в верхнем воздушном зазоре и, как следствие, к увеличению потока 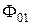и уменьшению магнитного напряжения на этом воздушном зазоре. Последнее неизбежно приводит к снижению потока .
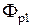Для нижнего воздушного зазора при указанном изменении D, магнитное сопротивление увеличится, соответственно поток 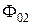уменьшится, а поток 
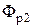возрастет.
С учетом сказанного можно составить магнитную цепь, моделирующую магнитную систему ДТИП (рис. 2.2).
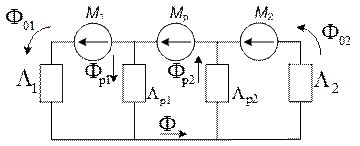
Рис. 2.2. Магнитная цепь, моделирующая магнитную систему ДТИП:
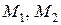и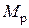 
– МДС, обеспечивающие проведение магнитных потоков соответственно 
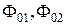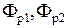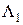и 
; 
и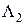 
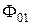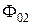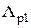– магнитные проводимости трубок потока вероятных путей магнитных потоков соответственно и ; 
и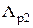 
– магнитные проводимости трубок вероятных путей магнитных потоков соответственно 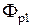и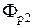
При составлении магнитной цепи, моделирующей магнитную систему ДТИП, использовался метод вероятных путей магнитного потока и методы теории магнитных цепей (прил. 1, пп. 1 и 2).
Этап 2. Определить проводимость трубок вероятных путей магнитного потока ДТИП.
Проводимость рабочего воздушного зазора между якорем 1 и кожухом 2 можно определить как проводимость трубок потока конца цилиндрического плунжера, близкого к концу концентрической трубки (прил. 1, п. 4) по формуле (П8). С учетом обозначений размеров, принятых на рис. 2.1, вводя обозначение с = h и r = d/2, выражение для проводимости 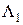можно записать в виде
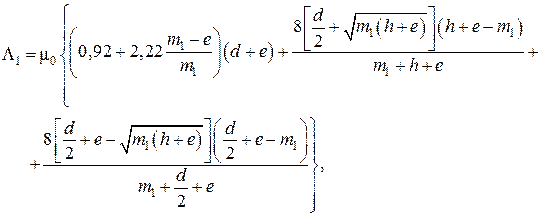(2.6)
где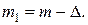 
Формулу для вычисления проводимости 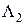получаем из формулы (2.6), заменив 
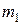на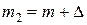 
.
Суммарную проводимость обоих рабочих зазоров обозначим через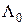 
и определим по формуле
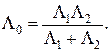(2.7)
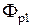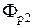Удельную проводимость l трубок путей магнитных потоков рассеяния и можно определить по формуле (П1.7), см. прил. 1, п. 5:
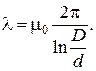(2.8)
Этап 3. Определить формулы для расчета таких конструктивных параметров ДТИП, как толщина кожуха h, длина электрической обмотки одной секции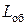 
, суммарная высота электрических обмоток 
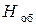, наружный диаметр D, длина корпуса 
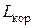(см. рис. 2.1).
При определении величины толщины кожуха решающим является обеспечение прохождения магнитного потока якоря в кожух без насыщения зоны перехода. При этом следует выполнять условие
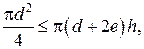
которое после преобразования примет вид
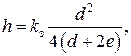(2.9)
где kз – коэффициент запаса.
Схематическое изображение ДТИП (см. рис. 2.1) позволяет составить следующие размерные цепи:
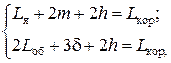
которые после преобразования дают формулу
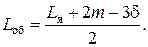(2.10)
Очевидна еще одна размерная цепь:
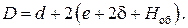(2.11)
Величину поперечного сечения окна обмотки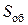 
можно определить геометрически
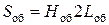(2.12)
и из условия заполнения окна обмотки
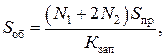(2.13)
где Sпр – поперечное сечение обмоточного привода;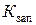 
– коэффициент заполнения окна обмотки обмоточным приводом.
Принимая во внимание, что площадь поперечного сечения провода Sпр через величину его диаметра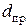 
выражается формулой
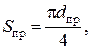
на основании формул (2.12) и (2.13) после преобразования получим следующее соотношение:
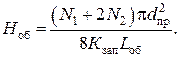(2.14)
Индуктивность ДТИП можно определить по формуле
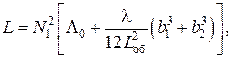(2.15)
где b1 и b2 – расчетные параметры, определенные по формулам:
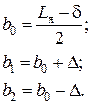(3.16)
Длина среднего витка обмотки возбуждения равна
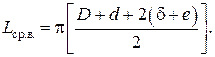(2.17)
Активная R и индуктивная X составляющие полного сопротивления Z обмотки возбуждения равны соответственно
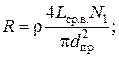(2.18)
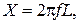(2.19)
где r – удельное электрическое сопротивление материала обмоточного провода; f – частота переменного напряжения, подаваемого на обмотку возбуждения.
Полное электрическое сопротивление переменному току обмотки возбуждения следует определить по формуле
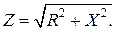(2.20)
Ток в обмотках возбуждения при подаче на нее переменного напряжения U равен
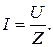(2.21)
Разностное напряжение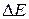 
на встречно соединенных вторичных индуктивных обмотках определяется по формуле
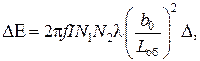(2.22)
где D – линейное перемещение якоря.
Длина корпуса ДТИП определяется по формуле
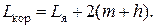(2.23)
Чувствительность ДТИП определяется по формуле
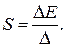(2.24)
2.2.2. Алгоритм расчета ДТИП
Расчет функции преобразования ДТИП выполнять в соответствии со схемой алгоритма, изображенной на рис. 2.3.
В результате расчета, наряду с выходным напряжением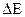 
, вычисляются недостающие конструктивные параметры 
; 
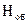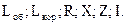
2.3. Пример расчета ДТИП
2.3.1. Исходные данные:
Блок 1:
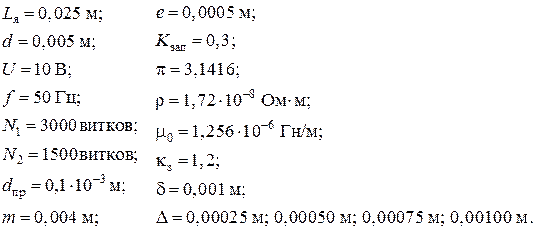
2 .3.2. Расчет ДТИП
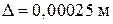
Блок 2: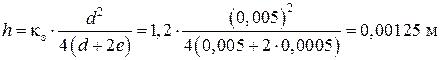 
Округляем из конструктивных соображений значение h до третьего знака после запятой в сторону увеличения: h = 0,002м.
Блок 3: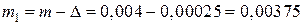 
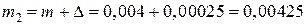
Рис. 2.3. Схема алгоритма расчета ДТИП
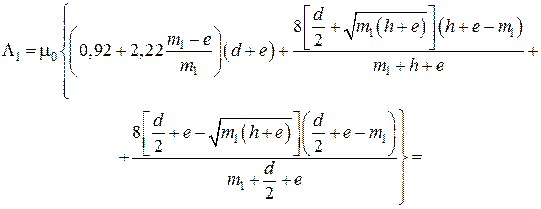
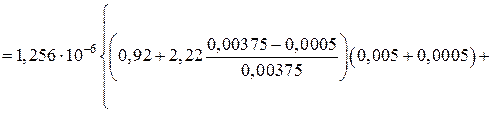
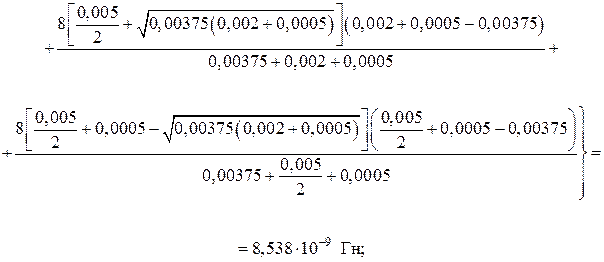
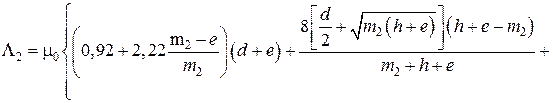
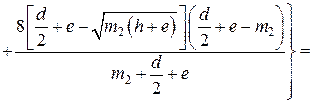
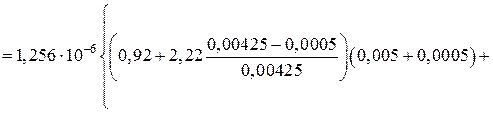
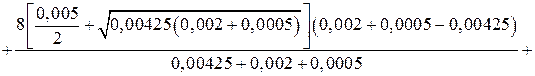
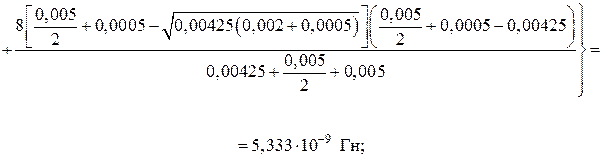
Блок 4: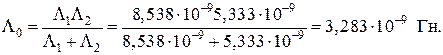 
Блок 5: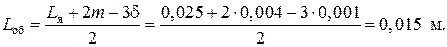 
Блок 6:
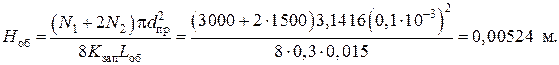
Блок 7: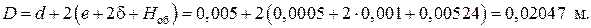 
Блок 8: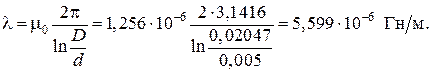 
Блок 9: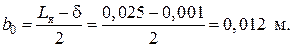 
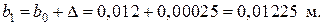
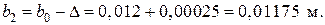
Блок 10: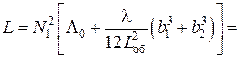 
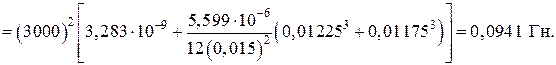
Блок 11: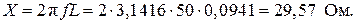 
Блок 12: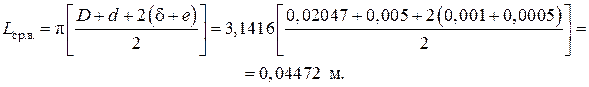 
Блок13: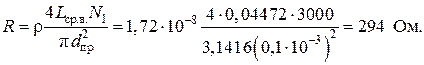 
Блок 14: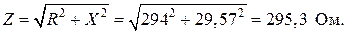 
Блок 15: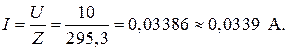 
Блок 16: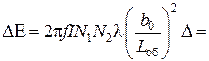 
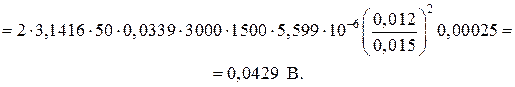
Блок 17: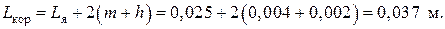 
Блок 18: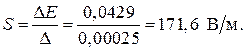 
Блок 19:
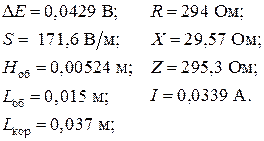
Проводя аналогичные расчеты для остальных значений D, получим следующие значения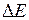 
и S:
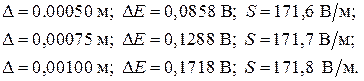
Функция преобразования ДТИП графически представлена на рис. 2.4.
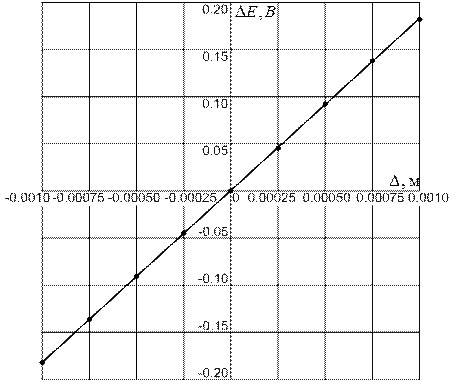
Рис. 2.4. График функции преобразования ДТИП
Тема 3. АНАЛИЗ ЭФФЕКТИВНОСТИ
ЭЛЕКТРОМАГНИТНЫХ ЭКРАНОВ
3.1. Описание анализируемого объекта
Для снижения уровня электромагнитной помехи, воздействующей на детали и узлы средств измерения, используются магнитостатические и электромагнитные экраны, изготовленные, соответственно, из магнитных и немагнитных металлов. Конструктивно экран представляет собой оболочку определенной толщины, как правило, простой геометрической формы. Чаще всего для этого применяются такие геометрические фигуры, как прямоугольный параллелепипед, прямой круговой цилиндр или сфера.
3.2. Задание на выполнение практической работы
Цель работы:
– для экрана заданной геометрической формы и размеров определить его эффективность в зависимости от выбранного материала, толщины экрана и частоты экранированного поля;
– полученные результаты оформить в виде таблиц и графиков, провести анализ влияния параметров экрана на его эффективность.
3.2.1. Этапы анализа
Этап 1. Для заданных преподавателем материалов экрана, формы и размеров выбрать формулы для определения эффективности экранирования с его помощью магнитостатических и электромагнитных полей помехи (прил. 3).
Этап 2. Для магнитостатических полей помехи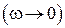 
рассчитать зависимости эффективности экранирования 
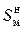от толщины экрана для различных заданных преподавателем материалов (значение относительной дифференциальной магнитной проницаемости 
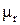для различных материалов приведены в прил. 3. Построить и проанализировать графики. Сделать выводы.
Этап 3. Для электромагнитных полей помехи рассчитать зависимость эффективности экранирования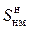 
от толщины экрана при различных частотах электромагнитного поля для различных заданных преподавателем материалов. Построить и проанализировать графики. Сделать выводы.
3.3. Пример расчета экранов
3.3.1. Расчетное задание
Определить эффективность электромагнитных экранов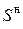 
для экранирования помех в виде магнитостатических и электромагнитных полей экранами со следующими конструктивными параметрами.
Форма экрана: прямоугольный параллелепипед.
Размеры: основание – прямоугольник со сторона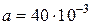ми 
м и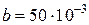 
м; высота 
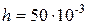м.
Материалы магнитостатических экранов – чугун серый и сталь электротехническая марки 2011.
Материалы электромагнитных экранов – медь электротехническая и латунь Л-68.
Рекомендуемые значения толщин:
– для магнитостатических экранов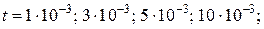 
;
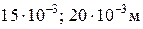– для электромагнитных экранов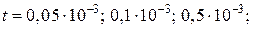 
.
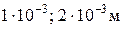Рекомендуемые значения частот для электромагнитных экранов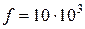 
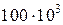Гц;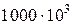 
Гц; 
Гц.
3.3.2. Расчет эффективности экранов
Эффективность магнитостатического экрана 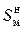определяем по формуле (П3.1) с учетом формулы (П3.7) (см. прил. 3).
Примечание. Использование формулы (П3.1) позволяет получить значение эффективности 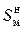экрана в децибелах (дБ), что существенно уменьшает область значения результатов. Это удобно для графического представления и в ряде других случаев. Однако для наглядности демонстрации влияния экрана на помеху эффективность 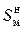можно представить в относительных единицах (о.е.), вычисляя в формуле (П3.1) только логарифмируемое выражение:
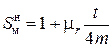, о.е.
Необходимые для расчета значения параметров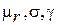 
приведены в прил. 3, п. 2.
Результаты расчетов представлены в виде табл. 3.1 и 3.2.
Таблица 3.1
Значения эффективности 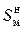магнитостатического экрана
из серого чугуна для различных толщин t его стенок
|
|
| |||||
| 0,001 | 0,003 | 0,005 | 0,010 | 0,015 | 0,020 | |
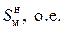
| 3,4 | 8,2 | 13,0 | 24,9 | 36,9 | 48,8 |
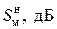
| 10,6 | 18,2 | 22,3 | 27,9 | 31,3 | 33,8 |
Таблица 3.2
Значения эффективности 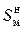магнитостатического экрана из
электротехнической стали марки 2011 для различных толщин t его стенок
|
|
| |||||
| 0,001 | 0,003 | 0,005 | 0,010 | 0,015 | 0,020 | |
|
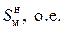
| 24,0 | 47,0 | 116 | 231 | 346 | 461 |
|
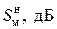
| 27,6 | 33,4 | 41,3 | 47,3 | 50,8 | 53,3 |
Эффективность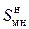 
электромагнитного экрана определяем по формуле (П3.4) с учетом формулы (П3.7).
Результаты расчетов представлены в виде табл. 3.3 и 3.4.
Таблица 3.3
Значения эффективности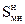 
электромагнитного экрана
из электротехнической меди для различных толщин t его стенок
и частот f электромагнитного поля помехи
|
| |||||
|
|
| ||||
| 0,05×10–3 | 0,1×10–3 | 0,5×10–3 | 1,0×10–3 | 2,0×10–3 | |
|
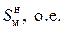
| 5,2 | 10,3 | 51,5 | 103 | 206 |
|
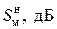
| 14,2 | 20,3 | 34,2 | 40,3 | 46,3 |
|
| |||||
|
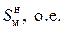
| 51,5 | 103 | 515 | 1030 | 2060 |
|
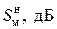
| 34,2 | 40,3 | 54,2 | 60,3 | 66,3 |
|
| |||||
|
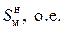
| 515 | 1030 | 5150 | 10300 | 20600 |
|
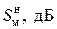
| 54,2 | 60,3 | 74,2 | 80,3 | 86,3 |
Таблица 3.4
Значения эффективности 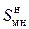электромагнитного экрана из латуни
марки Л- 68 для различных толщин t его стенок и частот f
электромагнитного поля помехи
|
| |||||
|
|
| ||||
| 0,05×10–3 | 0,1×10–3 | 0,5×10–3 | 1,0×10–3 | 2,0×10–3 | |
|
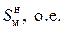
| 1,2 | 2,5 | 12,3 | 24,6 | 49,2 |
|
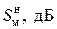
| 1,8 | 7,8 | 21,8 | 27,8 | 33,8 |
|
| |||||
|
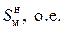
| 12,3 | 24,6 | 123 | 246 | 492 |
|
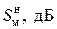
| 21,8 | 27,8 | 41,8 | 47,8 | 53,8 |
|
| |||||
|
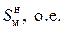
| 123 | 246 | 1230 | 2460 | 4920 |
|
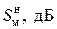
| 41,8 | 47,8 | 61,8 | 67,8 | 73,8 |
3.3.3. Сравнительный анализ эффективности экранов
На рис. 3.1 и 3.2 построены графики зависимостей эффективности, рассчитанных экранов при различных толщинах t их стенок и различных частотах f электромагнитного поля помехи.
Результаты анализа эффективности 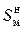магнитостатических экранов.
1. Эффективность 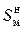растет с ростом толщины стен экрана. Так, например, увеличение толщины стенки t с 3 до 10 мм приводит независимо от материала экрана к росту эффективности в о.е. более чем в 3 раза.
2. Большое влияние на эффективность 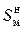оказывает материал экрана (его относительная дифференциальная магнитная проницаемость 
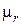). Так, например, для одинаковых по геометрическим размерам магнитостатических экранов из серого чугуна ( 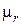= 215 о.е.) и стали электротехнической марки 2011 ( 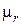= 2070 о.е.) эффективность 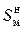в о.е. (при значении толщины t = 0,005 м) для стали 2011 составляет 116 о.е., тогда как для чугуна только 13 о.е., что в 8,9 раза больше (см. табл. 3.1 и 3.2).
3. Из графиков рис. 3.1 видно, что при одинаковой эффективности, например, 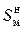= 30 дБ магнитостатических экранов, выполненных из чугуна и стали 2011 при одинаковых заданных геометрических размерах, a, b и с, толщина стенки экрана из стали 2011 составляет примерно t = 0,0015 м,
а для чугунного экрана около t = 0,014 м. При этом масса чугунного экрана примерно в 8 раз больше, чем аналогичного экрана из стали 2011.
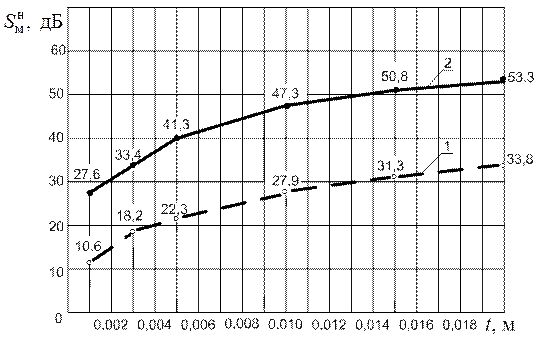
Рис. 3.1. Графики зависимостей эффективности магнитостатического экрана от толщины t его стенок, изготовленных из различных материалов:
1 – серый чугун; 2 – электротехническая сталь марки 2011
Результаты анализа эффективности 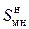электромагнитных экранов.
1. Эффективность 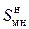растет с ростом толщины стенки экрана. Так, например, увеличение толщины стенки t с 0,05×10–3 до 0,5×10–3 м при f = 100×103 Гц приводит к увеличению эффективности в о.е. экрана из меди с 51,5 до 515 о.е., а экрана из латуни – с 12,3 до 123 о.е.
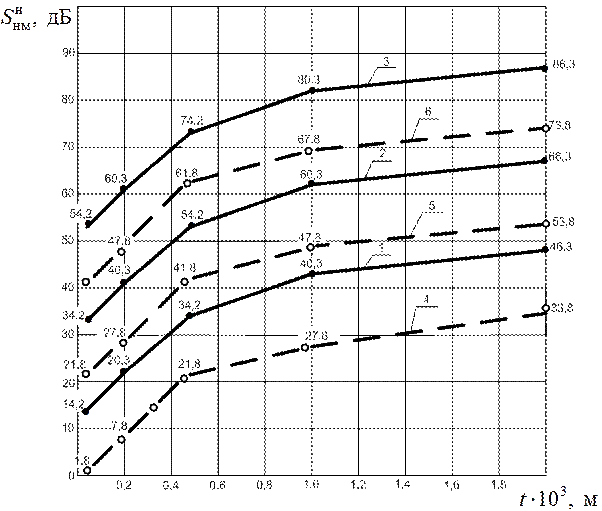
Рис. 3.2. Графики зависимостей эффективности электромагнитного экрана
от толщины t его стенок и частот f электромагнитного поля помехи для
различных материалов экранов:
––– –электротехническая медь (кривая 1 для f =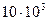 
Гц; кривая 2 для f = 
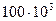Гц; кривая 3 для f = 
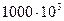Гц); – – – – латунь марки Л-68 (кривая 4 для f = 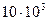Гц; кривая 5 для f = 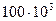Гц; кривая 6 для f = 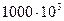Гц)
2. Из приведенных данных очевидно, что кратность увеличения эффективности 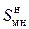с ростом толщины его стенки t не зависит от материала экрана.
3. Однако само значение эффективности 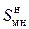существенно зависит от свойств материала экрана (в частности, от удельной электрической проводимости 
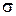). Так, например, для рассматриваемого экрана с толщиной стенки t = 0,5 мм, изготовленного из меди и латуни при f = 100×103 Гц эффективность 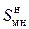составляет соответственно 515 и 123 о.е.
4. Эффективность 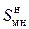сильно зависит от частоты электромагнитного поля помехи. Так, например, для рассматриваемого экрана из меди толщиной t = 0,5×10-3м увеличение частоты помехи с f = 10×103 Гц до f =100×103 Гц приводит к увеличению эффективности 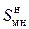с 51,5 до 515 о.е. Кратность увеличения 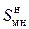равна 10.
5. Кратность увеличения эффективности 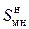при росте частоты электромагнитной помехи не зависит от свойств материала экрана. Так, например, для рассматриваемого экрана, сделанного из латуни, толщиной t = 0,5×10–3 м увеличение частоты помехи с f = 10×103 Гц до f = 100×103 Гц приводит к увеличению эффективности 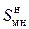с 12,3 до 123 о.е. Кратность увеличения 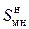равна 10. Для подтверждения сделанного вывода сравним полученную кратность 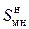с кратностью, полученной в п. 4, которая тоже равна 10.
6. Анализ графика рис. 3.2 позволяет заключить, что использование в качестве материала экрана меди вместо латуни позволит снизить массу экрана. Так, например, при одинаковой эффективности 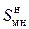= 50 дБ f = 100×103 Гц толщина стенки медного экрана t = 0,4 мм, а латунного – t = 1,3 мм, что приводит к увеличению массы латунного экрана, по сравнению с медным, более чем в 3 раза.