Постановка задачи о максимальном потоке.
Имеется сеть, которая задана множеством вершин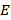 
и множеством дуг или рёбер 
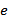, содержащих некоторые пары вершин 
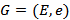. Можно рассматривать симметрический граф (хотя это не обязательно).
Пусть вершины графа обозначены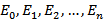 
. Каждая из них характеризуется интенсивностью 
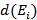, причём если 
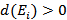, то вершина является источником, если 
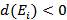- стоком, если 
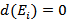, то промежуточной.
Сеть используется для перемещения предметов, веществ и так далее. Пропускная способность каждой дуги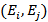 
равна 
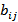. Величина 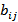представляет собой максимальное количество вещества, которое пропустить сеть по дуге 
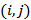в единицу времени.
Будем считать, что сеть имеет один источник и один сток. Остальные вершины – промежуточные, то есть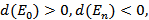 
.
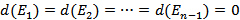Необходимо для данной сети определить, какой максимальный поток может быть направлен из вершины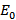 
в вершину 
.
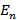Если считать, что по каждой дуге в единицу времени перемещается поток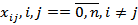 
, то поток всей сети будет представлять совокупность потоков 
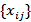по всем дугам сети.
Пусть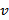 
– величина потока, перемещаемого по всем возможным путям.
С учётом этого задачу о максимальном потоке в формализованном виде можно записать следующим образом:
| где |
Найти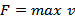 
, (3.1)
при ограничениях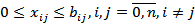 
, (3.3)
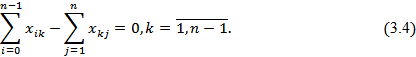
Условие (3.1) характеризует величину максимального потока, который равен количеству вещества, вытекающего из источника, либо втекающего в сток (3.2) – условие изменения переменной (должна быть положительным числом и не должна превышать пропускной способности дуги). Условие (3.3) показывает, что при проходе через вершину, количество вещества не уменьшается и не увеличивается.
Ключевым понятием при определении величины максимального потока сети является понятие разреза.
Чтобы дать его определение, разобьём всё множество вершин сети на два подмножества, которые не пересекаются между собо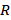й 
и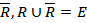 
. Причём 
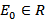, a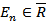 
. Выделим все дуги, начальные вершины которых принадлежат подмножеству 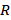, а конечные – подмножеству 
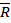. Эти дуги будут определять разрез 
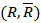, который отделяет источник 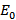от стока .
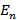Разрез – это некоторое подмножество дуг (рёбер, дуг и рёбер) сети, начальные вершины которых относятся к подмножеству вершин 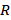, содержащих источник 
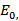, а конечные вершины – к подмножеству вершин 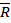, содержащих сток .
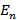Например, имеется сеть
| E0 |
| E5 |
| E1 |
| E3 |
| E2 |
| E4 |
На данной сети вершина 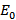– источник, а вершина 
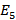– сток. Вершины 
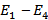– промежуточные. Разобьём всё множество вершин на два подмножества: подмножество 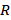включает вершины 
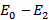, а подмножество 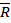– вершины 
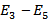. Дуг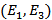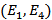и 
, 
и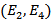 
образуют разрез, отделяющий источник от стока
| E0 |
| E5 |
| E1 |
| E3 |
| E2 |
| E4 |
|
|
|
|
Каждый из разрезов характеризуется определённой пропускной способностью, равной сумме пропускных способностей дуг (рёбер, дуг и рёбер), в него входящих
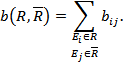
Любой путь из источника в сток обязательно содержит дугу, которая входит в разрез 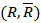, а удалив все дуги разреза 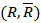, мы, тем самым. Блокируем все пути из 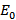в 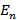. Так как пропускная способность пути определяется наименьшей из пропускных способностей дуг, входящих в этот путь, то величина потока, перемещаемого по всем возможным путям из 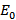в 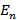, не может превышать пропускной способности любого разреза. То есть
.
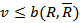Таким образом, если удастся построить поток, у которого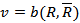 
, то этот поток и будет максимальным, а разрез – разрезом с минимальной пропускной способностью.
Учитывая это, можно сформулировать теорему о максимальном потоке (без доказательства).
Вопросы для самоконтроля.
1. Продолжите выражение:
a. Математически конечным графом называют ….
b. Дугой называется ….
c. Неориентированная пара вершин графа называется…
d. Если две дуги или ребра имеют хотя бы одну общую вершину, то они называются…
e. Граф называется ориентированным, если ….
f. Смешанным называется граф …
2. Опишите алгоритм Дейкстры.
3. Запишите задачу о максимальном потоке в формализованном виде.
Список литературы:
1. Иванов С. Н Математические методы исследования операций: Учеб. пособие. – Донецк: Донецкий национальный университет, 2003. – 688 с.
2. Христиановский В.В., Ходыкин В.Ф., Преображенский А.А. Задачи по математическому программированию: теория и практика. – Донецк: Дон НУ, 2003, 252 с.